Balbharti Maharashtra State Board Class 10 Maths Solutions
covers the Practice Set 3.1 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 3 Arithmetic Progression.
Question 1.
Which of the following sequences are A.P.? If they are A.P. find the common difference.
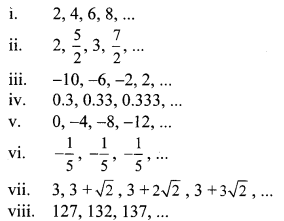
Solution:
i. The given sequence is 2, 4, 6, 8,…
Here, t1 = 2, t2 = 4, t3 = 6, t4 = 8
∴ t2 – t1 = 4 – 2 = 2
t3 – t2 = 6 – 4 = 2
t4 – t3 = 8 – 6 = 2
∴ t2 – t1 = t3 – t2 = … = 2 = d = constant
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = 2.
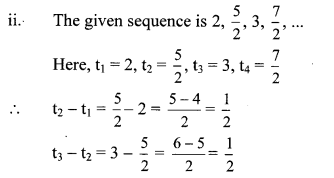
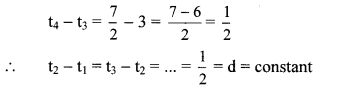
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = \(\frac { 1 }{ 2 } \).
iii. The given sequence is -10, -6, -2, 2,…
Here, t1 = -10, t2 = – 6, t3 = -2, t4 = 2
∴ t2 – t1 = -6 – (-10) = -6 + 10 = 4
t3 – t2 = -2 -(-6) = -2 + 6 = 4
t4 – t3 = 2 – (-2) = 2 + 2 = 4
∴ t2 – t1 = t3 – t2 = … = 4 = d = constant
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = 4.
iv. The given sequence is 0.3, 0.33, 0.333,…
Here, t1 = 0.3, t2 = 0.33, t3 = 0.333
∴ t2 -t1 = 0.33 – 0.3 = 0.03
t3 – t2 = 0.333 – 0.33 = 0.003
∴ t2 – t1 ≠ t3 – t2
The difference between two consecutive terms is not constant.
∴ The given sequence is not an A.P.
v. The given sequence is 0, -4, -8, -12,…
Here, t1 = 0, t2 = -4, t3 = -8, t4 = -12
∴ t2 – t1 = -4 – 0 = -4
t3 – t2 = -8 – (-4) = -8 + 4 = -4
t4 – t3 = -12 – (-8) = -12 + 8 = -4
∴ t2 – t1 = t3 – t2 = … = —4 = d = constant
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = -4.
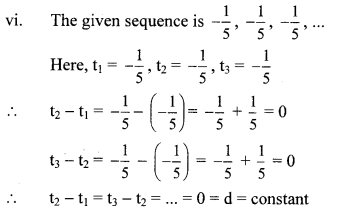
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = 0.
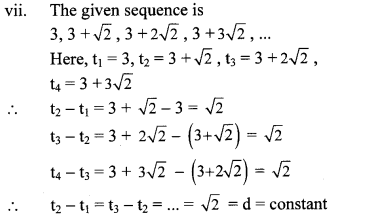
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = √2.
viii. The given sequence is 127, 132, 137,…
Here, t1 = 127, t2 = 132, t3 = 137
∴ t2 – t1 = 132 – 127 = 5
t3 – t2 = 137 – 132 = 5
∴ t2 – t1 = t3 – t2 = … = 5 = d = constant
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = 5.
Question 2.
Write an A.P. whose first term is a and common difference is d in each of the following.
i. a = 10, d = 5
ii. a = -3, d = 0
iii. a = -7, d = \(\frac { 1 }{ 2 } \)
iv. a = -1.25, d = 3
v. a = 6, d = -3
vi. a = -19, d = -4
Solution:
i. a = 10, d = 5 …[Given]
∴ t1 = a = 10
t2 = t1 + d = 10 + 5 = 15
t3 = t2 + d = 15 + 5 = 20
t4 = t3 + d = 20 + 5 = 25
∴ The required A.P. is 10,15, 20, 25,…
ii. a = -3, d = 0 …[Given]
∴ t1 = a = -3
t2 = t1 + d = -3 + 0 = -3
t3 = t2 + d = -3 + 0 = -3
t4 = t3 + d = -3 + 0 = -3
∴ The required A.P. is -3, -3, -3, -3,…
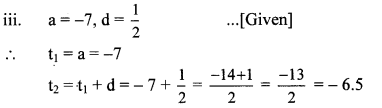
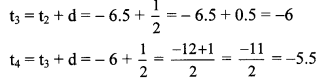
∴ The required A.P. is -7, – 6.5, – 6, – 5.5,
iv. a = -1.25, d = 3 …[Given]
t1 = a = -1.25
t2 = t1 + d = – 1.25 + 3 = 1.75
t3 = t2 + d = 1.75 + 3 = .4.75
t4 = t3 + d = 4.75 + 3 = 7.75
∴ The required A.P. is -1.25, 1.75, 4.75, 7.75,…
v. a = 6, d = -3 …[Given]
∴ t1 = a = 6
t2 = t1 + d = 6 – 3 = 3
t3 = t2 + d = 3 – 3 = 0
t4 = t3 + d = 0- 3 = -3
∴ The required A.P. is 6, 3, 0, -3,…
vi. a = -19, d = -4 …[Given]
t1 = a = -19
t2 = t1 + d = -19 – 4 = -23
t3 = t2 + d = -23 – 4 = -27
t4 = t3 + d = -27 – 4 = -31
∴ The required A.P. is -19, -23, -27, -31,…
Question 3.
Find the first term and common difference for each of the A.P.
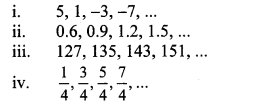
Solution:
i. The given A.P. is 5, 1,-3,-7,…
Here, t1 = 5, t2 = 1
∴ a = t1 = 5 and
d = t2 – t1 = 1 – 5 = -4
∴ first term (a) = 5,
common difference (d) = -4
ii. The given A.P. is 0.6, 0.9, 1.2, 1.5,…
Here, t1 = 0.6, t2 = 0.9
∴ a = t1 = 0.6 and
d = t2 – t1 = 0.9 – 0.6 = 0.3
∴ first term (a) = 0.6,
common difference (d) = 0.3
iii. The given A.P. is 127, 135, 143, 151,…
Here, t1 = 127, t2 = 135
∴ a = t1 = 127 and
d = t2 – t1 = 135 – 127 = 8
∴ first term (a) = 127,
common difference (d) = 8

Question 1.
Complete the given pattern. Look at the pattern of the numbers. Try to find a rule to obtain the next number from its preceding number. Write the next numbers. (Textbook pg, no. 55 and 56)
Answer:
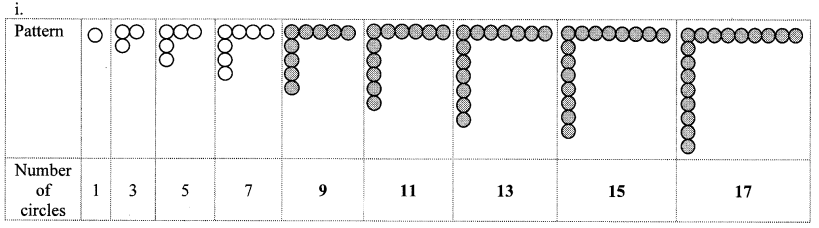
Every pattern is formed by adding a circle in horizontal and vertical rows to the preceding pattern.
∴ The sequence for the above pattern is 1,3, 5, 7, 9,11,13,15,17,….
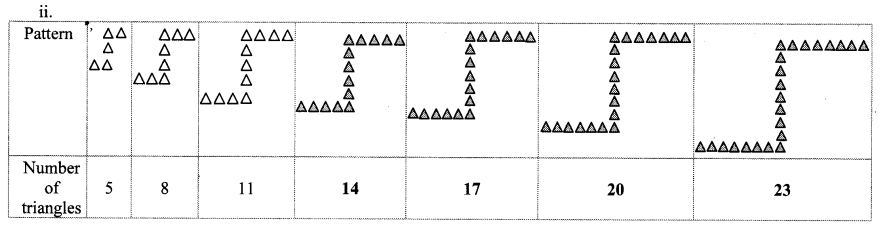
Every pattern is formed by adding 2 triangles horizontally and 1 triangle vertically to the preceding pattern.
∴ The sequence for the above pattern is 5,8,11,14,17,20,23,…
Question 2.
Some sequences are given below. Show the positions of the terms by t1, t2, t3,…
Answer:
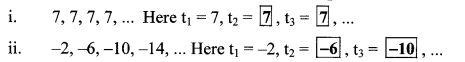
Question 3.
Some sequences are given below. Check whether there is any rule among the terms. Find the similarity between two sequences. To check the rule for the terms of the sequence look at the arrangements and fill the empty boxes suitably. (Textbook pg. no. 56 and 57)
i. .1,4,7,10,13,…
ii. 6,12,18,24,…
iii. 3,3,3,3,…
iv. 4, 16, 64,…
v. -1, -1.5, -2, -2.5,…
vi. 13, 23, 33, 43
Answer:
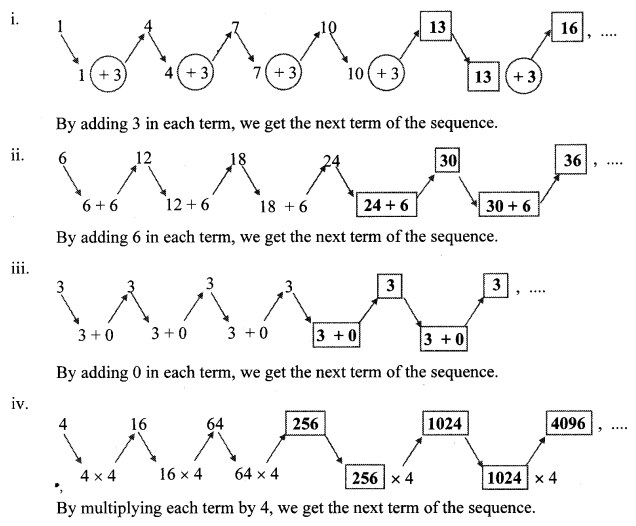
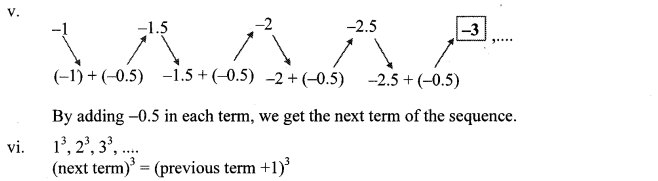
The similarity in the sequences i., ii., iii. and v. is that the next term is obtained by adding a particular fixed number to the previous term.
Note : A Geometric Progression is a sequence in which the ratio of any two consecutive terms is a constant,
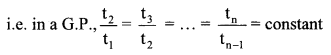
Sequence iv. is a geometric progression.
Question 4.
Write one example of finite and infinite A.P. each. (Textbook pg. no. 59)
Answer:
Finite A.P.:
Even natural numbers from 4 to 50:
4, 6, 8, ………………. 50.
Infinite A. P.:
Positive multiples of 5:
5, 10, 15, ……………..
covers the Practice Set 3.1 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 3 Arithmetic Progression.
Question 1.
Which of the following sequences are A.P.? If they are A.P. find the common difference.
Solution:
i. The given sequence is 2, 4, 6, 8,…
Here, t1 = 2, t2 = 4, t3 = 6, t4 = 8
∴ t2 – t1 = 4 – 2 = 2
t3 – t2 = 6 – 4 = 2
t4 – t3 = 8 – 6 = 2
∴ t2 – t1 = t3 – t2 = … = 2 = d = constant
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = 2.
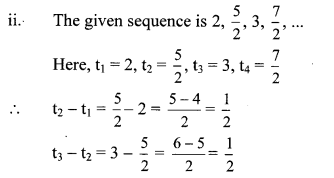
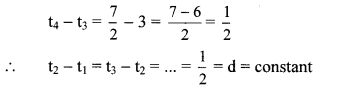
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = \(\frac { 1 }{ 2 } \).
iii. The given sequence is -10, -6, -2, 2,…
Here, t1 = -10, t2 = – 6, t3 = -2, t4 = 2
∴ t2 – t1 = -6 – (-10) = -6 + 10 = 4
t3 – t2 = -2 -(-6) = -2 + 6 = 4
t4 – t3 = 2 – (-2) = 2 + 2 = 4
∴ t2 – t1 = t3 – t2 = … = 4 = d = constant
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = 4.
iv. The given sequence is 0.3, 0.33, 0.333,…
Here, t1 = 0.3, t2 = 0.33, t3 = 0.333
∴ t2 -t1 = 0.33 – 0.3 = 0.03
t3 – t2 = 0.333 – 0.33 = 0.003
∴ t2 – t1 ≠ t3 – t2
The difference between two consecutive terms is not constant.
∴ The given sequence is not an A.P.
v. The given sequence is 0, -4, -8, -12,…
Here, t1 = 0, t2 = -4, t3 = -8, t4 = -12
∴ t2 – t1 = -4 – 0 = -4
t3 – t2 = -8 – (-4) = -8 + 4 = -4
t4 – t3 = -12 – (-8) = -12 + 8 = -4
∴ t2 – t1 = t3 – t2 = … = —4 = d = constant
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = -4.
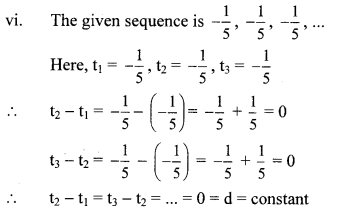
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = 0.
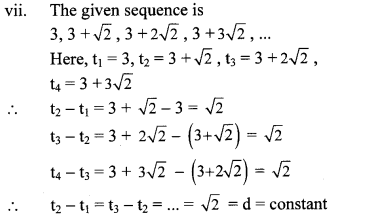
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = √2.
viii. The given sequence is 127, 132, 137,…
Here, t1 = 127, t2 = 132, t3 = 137
∴ t2 – t1 = 132 – 127 = 5
t3 – t2 = 137 – 132 = 5
∴ t2 – t1 = t3 – t2 = … = 5 = d = constant
The difference between two consecutive terms is constant.
∴ The given sequence is an A.P. and common difference (d) = 5.
Question 2.
Write an A.P. whose first term is a and common difference is d in each of the following.
i. a = 10, d = 5
ii. a = -3, d = 0
iii. a = -7, d = \(\frac { 1 }{ 2 } \)
iv. a = -1.25, d = 3
v. a = 6, d = -3
vi. a = -19, d = -4
Solution:
i. a = 10, d = 5 …[Given]
∴ t1 = a = 10
t2 = t1 + d = 10 + 5 = 15
t3 = t2 + d = 15 + 5 = 20
t4 = t3 + d = 20 + 5 = 25
∴ The required A.P. is 10,15, 20, 25,…
ii. a = -3, d = 0 …[Given]
∴ t1 = a = -3
t2 = t1 + d = -3 + 0 = -3
t3 = t2 + d = -3 + 0 = -3
t4 = t3 + d = -3 + 0 = -3
∴ The required A.P. is -3, -3, -3, -3,…
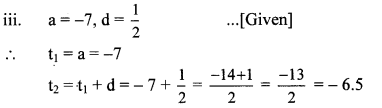
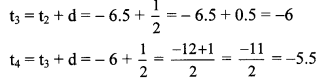
∴ The required A.P. is -7, – 6.5, – 6, – 5.5,
iv. a = -1.25, d = 3 …[Given]
t1 = a = -1.25
t2 = t1 + d = – 1.25 + 3 = 1.75
t3 = t2 + d = 1.75 + 3 = .4.75
t4 = t3 + d = 4.75 + 3 = 7.75
∴ The required A.P. is -1.25, 1.75, 4.75, 7.75,…
v. a = 6, d = -3 …[Given]
∴ t1 = a = 6
t2 = t1 + d = 6 – 3 = 3
t3 = t2 + d = 3 – 3 = 0
t4 = t3 + d = 0- 3 = -3
∴ The required A.P. is 6, 3, 0, -3,…
vi. a = -19, d = -4 …[Given]
t1 = a = -19
t2 = t1 + d = -19 – 4 = -23
t3 = t2 + d = -23 – 4 = -27
t4 = t3 + d = -27 – 4 = -31
∴ The required A.P. is -19, -23, -27, -31,…
Question 3.
Find the first term and common difference for each of the A.P.
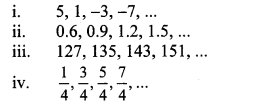
Solution:
i. The given A.P. is 5, 1,-3,-7,…
Here, t1 = 5, t2 = 1
∴ a = t1 = 5 and
d = t2 – t1 = 1 – 5 = -4
∴ first term (a) = 5,
common difference (d) = -4
ii. The given A.P. is 0.6, 0.9, 1.2, 1.5,…
Here, t1 = 0.6, t2 = 0.9
∴ a = t1 = 0.6 and
d = t2 – t1 = 0.9 – 0.6 = 0.3
∴ first term (a) = 0.6,
common difference (d) = 0.3
iii. The given A.P. is 127, 135, 143, 151,…
Here, t1 = 127, t2 = 135
∴ a = t1 = 127 and
d = t2 – t1 = 135 – 127 = 8
∴ first term (a) = 127,
common difference (d) = 8

Question 1.
Complete the given pattern. Look at the pattern of the numbers. Try to find a rule to obtain the next number from its preceding number. Write the next numbers. (Textbook pg, no. 55 and 56)
Answer:

Every pattern is formed by adding a circle in horizontal and vertical rows to the preceding pattern.
∴ The sequence for the above pattern is 1,3, 5, 7, 9,11,13,15,17,….

Every pattern is formed by adding 2 triangles horizontally and 1 triangle vertically to the preceding pattern.
∴ The sequence for the above pattern is 5,8,11,14,17,20,23,…
Question 2.
Some sequences are given below. Show the positions of the terms by t1, t2, t3,…
Answer:
Question 3.
Some sequences are given below. Check whether there is any rule among the terms. Find the similarity between two sequences. To check the rule for the terms of the sequence look at the arrangements and fill the empty boxes suitably. (Textbook pg. no. 56 and 57)
i. .1,4,7,10,13,…
ii. 6,12,18,24,…
iii. 3,3,3,3,…
iv. 4, 16, 64,…
v. -1, -1.5, -2, -2.5,…
vi. 13, 23, 33, 43
Answer:

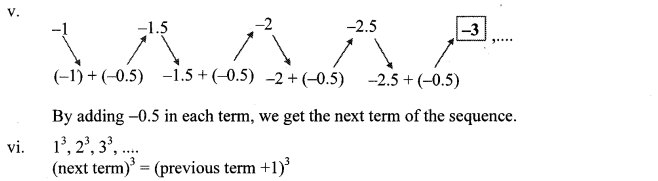
The similarity in the sequences i., ii., iii. and v. is that the next term is obtained by adding a particular fixed number to the previous term.
Note : A Geometric Progression is a sequence in which the ratio of any two consecutive terms is a constant,
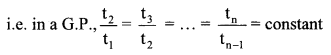
Sequence iv. is a geometric progression.
Question 4.
Write one example of finite and infinite A.P. each. (Textbook pg. no. 59)
Answer:
Finite A.P.:
Even natural numbers from 4 to 50:
4, 6, 8, ………………. 50.
Infinite A. P.:
Positive multiples of 5:
5, 10, 15, ……………..