Balbharti Maharashtra State Board Class 10 Maths Solutions
covers the Practice Set 3.3 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 3 Arithmetic Progression.
Arithmetic Progression Practice Set 3.3 Question 1.
First term and common difference of an A.P. are 6 and 3 respectively; find S27.
Solution:
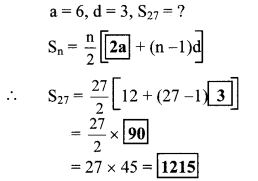
Arithmetic Progression Class 10 Practice Set 3.3 Question 2.
Find the sum of first 123 even natural numbers.
Solution:
The even natural numbers are 2, 4, 6, 8,…
The above sequence is an A.P.
∴ a = 2, d = 4 – 2 = 2, n = 123
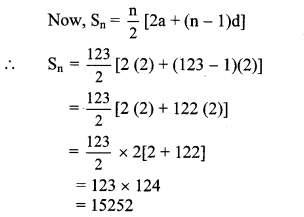
∴ The sum of first 123 even natural numbers is 15252.
Practice Set 3.3 Question 3.
Find the sum of all even numbers between 1 and 350.
Solution:
The even numbers between 1 and 350 are 2, 4, 6,…, 348.
The above sequence is an A.P.
∴ a = 2, d = 4 – 2 = 2, tn = 348
Since, tn = a + (n – 1)d
∴ 348 = 2 + (n – 1)2
∴ 348 – 2 = (n – 1)2
∴ 346 = (n – 1)2
∴ n – 1 = \(\frac { 346 }{ 2 } \)
∴ n – 1 = 173
∴ n = 173 + 1 = 174
Now, Sn = \(\frac { n }{ 2 } \) [2a + (n – 1)d]
∴ S174 = \(\frac { 174 }{ 2 } \) [2 (2) + (174 – 1)2]
= 87(4 + 173 × 2)
= 87(4 + 346)
= 87 × 350
∴ S174 = 30450
∴ The sum of all even numbers between 1 and 350 is 30450.
Arithmetic Progression 3.3 Question 4.
In an A.P. 19th term is 52 and 38th term is 128, find sum of first 56 terms.
Solution:
For an A.P., let a be the first term and d be the common difference.
t19 = 52, t38 = 128 …[Given]
Since, tn = a + (n – 1)d
∴ t19 = a + (19 – 1)d
∴ 52 = a + 18d
i.e. a + 18d = 52 …(i)
Also, t38 = a + (38 – 1)d
∴ 128 = a + 37d
i.e. a + 37d = 128 …(ii)
Adding equations (i) and (ii), we get

3 Arithmetic Progression Question 5.
Complete the following activity to find the sum of natural numbers between 1 to 140 which are divisible by 4.
Solution:
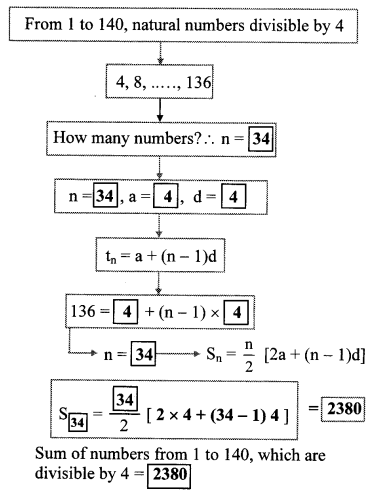
10th Algebra Practice Set 3.3 Question 6.
Sum of first 55 terms in an A.P. is 3300, find its 28th term.
Solution:
For an A.P., let a be the first term and d be the common difference.
S55 =3300 …[Given]
Since, Sn = \(\frac { n }{ 2 } \) [2a + (n – 1)d]
∴ S55 = \(\frac { 55 }{ 2 } \) [2a + (55 – 1)d]

Arithmetic Practice Set Question 7.
In an A.P. sum of three consecutive terms is 27 and their product is 504, find the terms. (Assume that three consecutive terms in A.P. are a – d, a, a + d.)
Solution:
Let the three consecutive terms in an A.P. be
a – d, a and a + d.
According to the first condition,
a – d + a + a + d = 27
∴ 3a = 27
∴ a = \(\frac { 27 }{ 3 } \)
∴ a = 9 ….(i)
According to the second condition,
(a – d) a (a + d) = 504
∴ a(a2 – d2) = 504
∴ 9(a2 – d2) = 504 …[From (i)]
∴ 9(81 – d2) = 504
∴ 81 – d2 = \(\frac { 504 }{ 9 } \)
∴ 81 – d2 = 56
∴ d2 = 81 – 56
∴ d2 = 25
Taking square root of both sides, we get
d = ± 5
When d = 5 and a =9,
a – d 9 – 5 = 4
a = 9
a + d 9 + 5 = 14
When d = -5 and a = 9,
a – d = 9 – (-5) = 9 + 5 = 14
a = 9
a + d = 9 – 5 = 4
∴ The three consecutive terms are 4, 9 and 14 or 14, 9 and 4.
10th Maths 1 Practice Set 3.3 Question 8.
Find four consecutive terms in an A.P. whose sum is 12 and sum of 3rd and 4th term is 14. (Assume the four consecutive terms in A.P. are a – d, a, a + d, a + 2d.)
Solution:
Let the four consecutive terms in an A.P. be
a – d, a, a + d and a + 2d.
According to the first condition,
a – d + a + a + d + a + 2d = 12
∴ 4a + 2d =12
∴ 2(2a + d) = 12
∴ 2a + d = \(\frac { 12 }{ 2 } \)
∴ 2a + d = 6 …(i)
According to the second condition,
a + d + a + 2d = 14
∴ 2a + 3d = 14 …(ii)
Subtracting equation (i) from (ii), we get
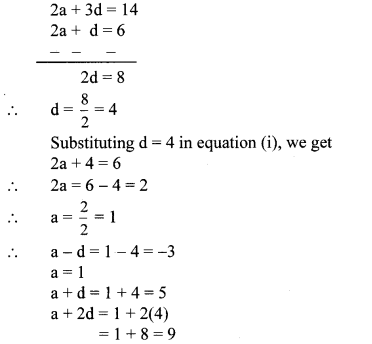
∴ The four consecutive terms are -3,1,5 and 9.
Math 1 Practice Set 3.3 Question 9.
If the 9th term of an A.P. is zero, then show that the 29th term is twice the 19th term.
To prove: t29 = 2t19
Proof:
For an A.P., let a be the first term and d be the common difference.
t9 = 0 …[Given]
Since, tn = a + (n – 1)d
∴ t9 = a + (9 – 1)d
∴ 0 = a + 8d
∴ a = -8d …(i)
Also, t19 = a + (19 – 1)d
= a + 18d
= -8d + 18d … [From (i)]
∴ t19 = 10d …(ii)
and t29 = a + (29 – 1)d
= a + 28d
= -8d + 28d …[From (i)]
∴ t29 = 20d = 2(10d)
∴ t29 = 2(t19) … [From (ii)]
∴ The 29th term is twice the 19th term.
10 Class Math Part 1 Practice Set 3.3 Question 1.
Find the sum of all odd numbers from 1 to 150. (Textbook pg, no. 71)
Solution:
Odd numbers from 1 to 150 are 1,3, 5, 7,…, 149
Here, difference between any two consecutive terms is 2.
∴ It is an A.P.
∴ a = 1, d = 2
Let us find how many odd numbers are there from 1 to 150, i.e. find the value of n if
tn = 149
tn = a + (n – 1)d
∴ 149 = 1 + (n – 1)2
∴ 149 – 1 = (n – 1)2
∴ \(\frac { 148 }{ 2 } \) = n – 1
∴ 74 = n – 1
∴ n = 74 + 1 = 75
ii. Now, let’s find the sum of 75 numbers
i. e. 1 + 3 + 5 + 7 + … + 149

covers the Practice Set 3.3 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 3 Arithmetic Progression.
Arithmetic Progression Practice Set 3.3 Question 1.
First term and common difference of an A.P. are 6 and 3 respectively; find S27.
Solution:
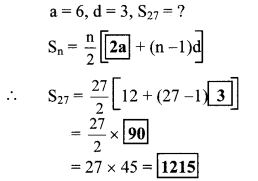
Arithmetic Progression Class 10 Practice Set 3.3 Question 2.
Find the sum of first 123 even natural numbers.
Solution:
The even natural numbers are 2, 4, 6, 8,…
The above sequence is an A.P.
∴ a = 2, d = 4 – 2 = 2, n = 123
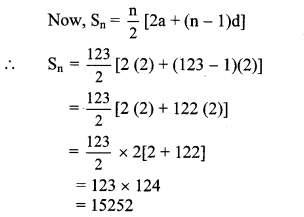
∴ The sum of first 123 even natural numbers is 15252.
Practice Set 3.3 Question 3.
Find the sum of all even numbers between 1 and 350.
Solution:
The even numbers between 1 and 350 are 2, 4, 6,…, 348.
The above sequence is an A.P.
∴ a = 2, d = 4 – 2 = 2, tn = 348
Since, tn = a + (n – 1)d
∴ 348 = 2 + (n – 1)2
∴ 348 – 2 = (n – 1)2
∴ 346 = (n – 1)2
∴ n – 1 = \(\frac { 346 }{ 2 } \)
∴ n – 1 = 173
∴ n = 173 + 1 = 174
Now, Sn = \(\frac { n }{ 2 } \) [2a + (n – 1)d]
∴ S174 = \(\frac { 174 }{ 2 } \) [2 (2) + (174 – 1)2]
= 87(4 + 173 × 2)
= 87(4 + 346)
= 87 × 350
∴ S174 = 30450
∴ The sum of all even numbers between 1 and 350 is 30450.
Arithmetic Progression 3.3 Question 4.
In an A.P. 19th term is 52 and 38th term is 128, find sum of first 56 terms.
Solution:
For an A.P., let a be the first term and d be the common difference.
t19 = 52, t38 = 128 …[Given]
Since, tn = a + (n – 1)d
∴ t19 = a + (19 – 1)d
∴ 52 = a + 18d
i.e. a + 18d = 52 …(i)
Also, t38 = a + (38 – 1)d
∴ 128 = a + 37d
i.e. a + 37d = 128 …(ii)
Adding equations (i) and (ii), we get

3 Arithmetic Progression Question 5.
Complete the following activity to find the sum of natural numbers between 1 to 140 which are divisible by 4.
Solution:

10th Algebra Practice Set 3.3 Question 6.
Sum of first 55 terms in an A.P. is 3300, find its 28th term.
Solution:
For an A.P., let a be the first term and d be the common difference.
S55 =3300 …[Given]
Since, Sn = \(\frac { n }{ 2 } \) [2a + (n – 1)d]
∴ S55 = \(\frac { 55 }{ 2 } \) [2a + (55 – 1)d]

Arithmetic Practice Set Question 7.
In an A.P. sum of three consecutive terms is 27 and their product is 504, find the terms. (Assume that three consecutive terms in A.P. are a – d, a, a + d.)
Solution:
Let the three consecutive terms in an A.P. be
a – d, a and a + d.
According to the first condition,
a – d + a + a + d = 27
∴ 3a = 27
∴ a = \(\frac { 27 }{ 3 } \)
∴ a = 9 ….(i)
According to the second condition,
(a – d) a (a + d) = 504
∴ a(a2 – d2) = 504
∴ 9(a2 – d2) = 504 …[From (i)]
∴ 9(81 – d2) = 504
∴ 81 – d2 = \(\frac { 504 }{ 9 } \)
∴ 81 – d2 = 56
∴ d2 = 81 – 56
∴ d2 = 25
Taking square root of both sides, we get
d = ± 5
When d = 5 and a =9,
a – d 9 – 5 = 4
a = 9
a + d 9 + 5 = 14
When d = -5 and a = 9,
a – d = 9 – (-5) = 9 + 5 = 14
a = 9
a + d = 9 – 5 = 4
∴ The three consecutive terms are 4, 9 and 14 or 14, 9 and 4.
10th Maths 1 Practice Set 3.3 Question 8.
Find four consecutive terms in an A.P. whose sum is 12 and sum of 3rd and 4th term is 14. (Assume the four consecutive terms in A.P. are a – d, a, a + d, a + 2d.)
Solution:
Let the four consecutive terms in an A.P. be
a – d, a, a + d and a + 2d.
According to the first condition,
a – d + a + a + d + a + 2d = 12
∴ 4a + 2d =12
∴ 2(2a + d) = 12
∴ 2a + d = \(\frac { 12 }{ 2 } \)
∴ 2a + d = 6 …(i)
According to the second condition,
a + d + a + 2d = 14
∴ 2a + 3d = 14 …(ii)
Subtracting equation (i) from (ii), we get
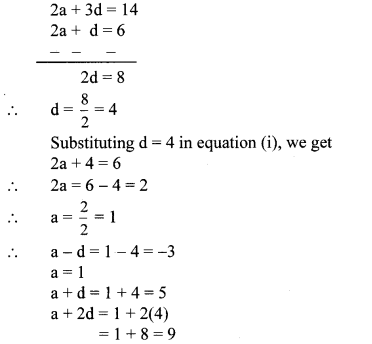
∴ The four consecutive terms are -3,1,5 and 9.
Math 1 Practice Set 3.3 Question 9.
If the 9th term of an A.P. is zero, then show that the 29th term is twice the 19th term.
To prove: t29 = 2t19
Proof:
For an A.P., let a be the first term and d be the common difference.
t9 = 0 …[Given]
Since, tn = a + (n – 1)d
∴ t9 = a + (9 – 1)d
∴ 0 = a + 8d
∴ a = -8d …(i)
Also, t19 = a + (19 – 1)d
= a + 18d
= -8d + 18d … [From (i)]
∴ t19 = 10d …(ii)
and t29 = a + (29 – 1)d
= a + 28d
= -8d + 28d …[From (i)]
∴ t29 = 20d = 2(10d)
∴ t29 = 2(t19) … [From (ii)]
∴ The 29th term is twice the 19th term.
10 Class Math Part 1 Practice Set 3.3 Question 1.
Find the sum of all odd numbers from 1 to 150. (Textbook pg, no. 71)
Solution:
Odd numbers from 1 to 150 are 1,3, 5, 7,…, 149
Here, difference between any two consecutive terms is 2.
∴ It is an A.P.
∴ a = 1, d = 2
Let us find how many odd numbers are there from 1 to 150, i.e. find the value of n if
tn = 149
tn = a + (n – 1)d
∴ 149 = 1 + (n – 1)2
∴ 149 – 1 = (n – 1)2
∴ \(\frac { 148 }{ 2 } \) = n – 1
∴ 74 = n – 1
∴ n = 74 + 1 = 75
ii. Now, let’s find the sum of 75 numbers
i. e. 1 + 3 + 5 + 7 + … + 149
