Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 2.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 2 Pythagoras Theorem.

Question 1.
In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.

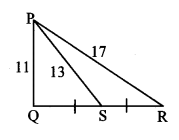
Solution:
In ∆PQR, point S is the midpoint of side QR. [Given]
∴ seg PS is the median.
∴ PQ² + PR² = 2 PS² + 2 SR² [Apollonius theorem]
∴ 11² + 17² = 2 (13)² + 2 SR²
∴ 121 + 289 = 2 (169)+ 2 SR²
∴ 410 = 338+ 2 SR²
∴ 2 SR² = 410 – 338
∴ 2 SR² = 72
∴ SR² = \(\frac { 72 }{ 2 } \) = 36
∴ SR = \(\sqrt{36}\) [Taking square root of both sides]
= 6 units Now, QR = 2 SR [S is the midpoint of QR]
= 2 × 6
∴ QR = 12 units

Question 2.
In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
Solution:
Let CD be the median drawn from the vertex C to side AB.
BD = \(\frac { 1 }{ 2 } \) AB [D is the midpoint of AB]
= \(\frac { 1 }{ 2 } \) × 10 = 5 units

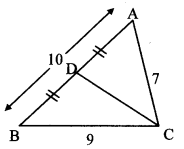
In ∆ABC, seg CD is the median. [Given]
∴ AC² + BC² = 2 CD² + 2 BD² [Apollonius theorem]
∴ 7² + 9² = 2 CD² + 2 (5)²
∴ 49 + 81 = 2 CD² + 2 (25)
∴ 130 = 2 CD² + 50
∴ 2 CD² = 130 – 50
∴ 2 CD² = 80
∴ CD² = \(\frac { 80 }{ 2 } \) = 40
∴ CD = \(\sqrt { 40 }\) [Taking square root of both sides]
= 2 \(\sqrt { 10 }\) units
∴ The length of the median drawn from point C to side AB is 2 \(\sqrt { 10 }\) units.

Question 3.
In the adjoining figure, seg PS is the median of APQR and PT ⊥ QR. Prove that,

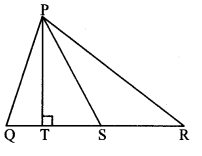
i. PR² = PS² + QR × ST + (\(\frac { QR }{ 2 } \))²
ii. PQ² = PS² – QR × ST + (\(\frac { QR }{ 2 } \))²
Solution:
i. QS = SR = \(\frac { 1 }{ 2 } \) QR (i) [S is the midpoint of side QR]

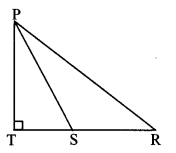
∴ In ∆PSR, ∠PSR is an obtuse angle [Given]
and PT ⊥ SR [Given, Q-S-R]
∴ PR² = SR² +PS² + 2 SR × ST (ii) [Application of Pythagoras theorem]
∴ PR² = (\(\frac { 1 }{ 2 } \) QR)² + PS² + 2 (\(\frac { 1 }{ 2 } \) QR) × ST [From (i) and (ii)]
∴ PR² = (\(\frac { QR }{ 2 } \))² + PS² + QR × ST
∴ PR² = PS² + QR × ST + (\(\frac { QR }{ 2 } \))²

ii. In.∆PQS, ∠PSQ is an acute angle and [Given]

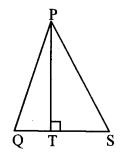
PT ⊥QS [Given, Q-S-R]
∴ PQ² = QS² + PS² – 2 QS × ST (iii) [Application of Pythagoras theorem]
∴ PR² = (\(\frac { 1 }{ 2 } \) QR)² + PS² – 2 (\(\frac { 1 }{ 2 } \) QR) × ST [From (i) and (iii)]
∴ PR² = (\(\frac { QR }{ 2 } \))² + PS² – QR × ST
∴ PR² = PS² – QR × ST + (\(\frac { QR }{ 2 } \))²

Question 4.
In ∆ABC, point M is the midpoint of side BC. If AB² + AC² = 290 cm, AM = 8 cm, find BC.

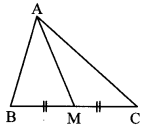
Solution:
In ∆ABC, point M is the midpoint of side BC. [Given]
∴ seg AM is the median.
∴ AB² + AC² = 2 AM² + 2 MC² [Apollonius theorem]
∴ 290 = 2 (8)² + 2 MC²
∴ 145 = 64 + MC² [Dividing both sides by 2]
∴ MC² = 145 – 64
∴ MC² = 81
∴ MC = \(\sqrt{81}\) [Taking square root of both sides]
MC = 9 cm
Now, BC = 2 MC [M is the midpoint of BC]
= 2 × 9
∴ BC = 18 cm

Question 5.
In the adjoining figure, point T is in the interior of rectangle PQRS. Prove that, TS² + TQ² = TP² + TR². (As shown in the figure, draw seg AB || side SR and A – T – B)

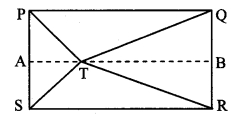
Given: ꠸PQRS is a rectangle.
Point T is in the interior of ꠸PQRS.
To prove: TS² + TQ² = TP² + TR²
Construction: Draw seg AB || side SR such that A – T – B.
Solution:
Proof:
꠸PQRS is a rectangle. [Given]
∴ PS = QR (i) [Opposite sides of a rectangle]
In ꠸ASRB,
∠S = ∠R = 90° (ii) [Angles of rectangle PQRS]
side AB || side SR [Construction]
Also ∠A = ∠S = 90° [Interior angle theorem, from (ii)]
∠B = ∠R = 90°
∴ ∠A = ∠B = ∠S = ∠R = 90° (iii)
∴ ꠸ASRB is a rectangle.
∴ AS = BR (iv) [Opposite sides of a rectanglel

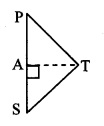
In ∆PTS, ∠PST is an acute angle
and seg AT ⊥ side PS [From (iii)]
∴ TP² = PS² + TS² – 2 PS.AS (v) [Application of Pythagoras theorem]
In ∆TQR., ∠TRQ is an acute angle
and seg BT ⊥ side QR [From (iii)]
∴ TQ² = RQ² + TR² – 2 RQ.BR (vi) [Application of pythagoras theorem]

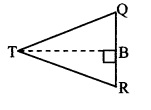
TP² – TQ² = PS² + TS² – 2PS.AS
-RQ² – TR² + 2RQ.BR [Subtracting (vi) from (v)]
∴ TP² – TQ² = TS² – TR² + PS²
– RQ² -2 PS.AS +2 RQ.BR
∴ TP² – TQ² = TS² – TR² + PS²
– PS² – 2 PS.BR + 2PS.BR [From (i) and (iv)]
∴ TP² – TQ² = TS² – TR²
∴ TS² + TQ² = TP² + TR²

Question 1.
In ∆ABC, ∠C is an acute angle, seg AD Iseg BC. Prove that: AB² = BC² + A² – 2 BC × DC. (Textbook pg. no. 44)
Given: ∠C is an acute angle, seg AD ⊥ seg BC.
To prove: AB² = BC² + AC² – 2BC × DC
Solution:
Proof:
∴ LetAB = c, AC = b, AD = p,

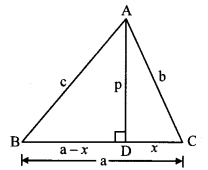
∴ BC = a, DC = x
BD + DC = BC [B – D – C]
∴ BD = BC – DC
∴ BD = a – x
In ∆ABD, ∠D = 90° [Given]
AB² = BD² + AD² [Pythagoras theorem]
∴ c² = (a – x)² + [P²] (i)
∴ c² = a² – 2ax + x² + [P²]
In ∆ADC, ∠D = 90° [Given]
AC² = AD² + CD² [Pythagoras theorem]
∴ b² = p² + [X²]
∴ p² = b² – [X²] (ii)
∴ c² = a² – 2ax + x² + b² – x² [Substituting (ii) in (i)]
∴ c² = a² + b² – 2ax
∴ AB² = BC² + AC² – 2 BC × DC

Question 2.
In ∆ABC, ∠ACB is an obtuse angle, seg AD ⊥ seg BC. Prove that: AB² = BC² + AC² + 2 BC × CD. (Textbook pg. no. 40 and 4.1)
Given: ∠ACB is an obtuse angle, seg AD ⊥ seg BC.
To prove: AB² = BC² + AC² + 2BC × CD
Solution:
Proof:

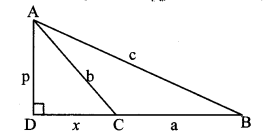
Let AD = p, AC = b, AB = c,
BC = a, DC = x
BD = BC + DC [B – C – D]
∴ BD = a + x
In ∆ADB, ∠D = 90° [Given]
AB² = BD² + AD² [Pythagoras theorem]
∴ c² = (a + x)² + p² (i)
∴ c² = a² + 2ax + x² + p²
Also, in ∆ADC, ∠D = 90° [Given]
AC² = CD² + AD² [Pythagoras theorem]
∴ b² = x² + p²
∴ p² = b² – x² (ii)
∴ c² = a² + 2ax + x² + b² – x² [Substituting (ii) in (i)]
∴ c² = a² + b² + 2ax
∴ AB² = BC² + AC² + 2 BC × CD

Question 3.
In ∆ABC, if M is the midpoint of side BC and seg AM ⊥seg BC, then prove that
AB² + AC² = 2 AM² + 2 BM². (Textbook pg, no. 41)
Given: In ∆ABC, M is the midpoint of side BC and seg AM ⊥ seg BC.
To prove: AB² + AC² = 2 AM² + 2 BM²
Solution:
Proof:

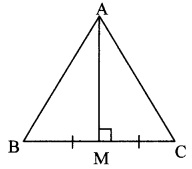
In ∆AMB, ∠M = 90° [segAM ⊥ segBC]
∴ AB2 = AM2 + BM2 (i) [Pythagoras theorem]
Also, in ∆AMC, ∠M = 90° [seg AM ⊥ seg BC]
∴ AC2 = AM2 + MC2 (ii) [Pythagoras theorem]
∴ AB² + AC² = AM² + BM² + AM² + MC² [Adding (i) and (ii)]
∴ AB² + AC² = 2 AM² + BM² + BM² [∵ BM = MC (M is the midpoint of BC)]
∴ AB² + AC² = 2 AM² + 2 BM²

Loading...

Submit Answer

Show Answer

Hide Answer