Balbharti Maharashtra State Board Class 10 Maths Solutions
covers the Practice Set 3.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 3 Circle.
Question 1.
Two circles having radii 3.5 cm and 4.8 cm touch each other internally. Find the distance between their centres.
Solution:
Let the two circles having centres P and Q touch each other internally at point R.
Here, QR = 3.5 cm, PR = 4.8 cm
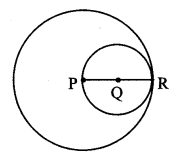
The two circles touch each other internally.
∴ By theorem of touching circles,
P – Q – R
PQ = PR – QR
= 4.8 – 3.5
= 1.3 cm
[The distance between the centres of circles touching internally is equal to the difference in their radii]
Question 2.
Two circles of radii 5.5 cm and 4.2 cm touch each other externally. Find the distance between their centres.
Solution:
Let the two circles having centres P and R touch each other externally at point Q.
Here, PQ = 5.5 cm, QR = 4.2 cm
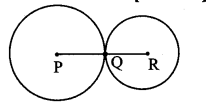
The two circles touch each other externally.
∴ By theorem of touching circles,
P – Q – R
PR = PQ + QR
= 5.5 + 4.2
= 9.7 cm
[The distance between the centres of the circles touching externally is equal to the sum of their radii]
Question 3.
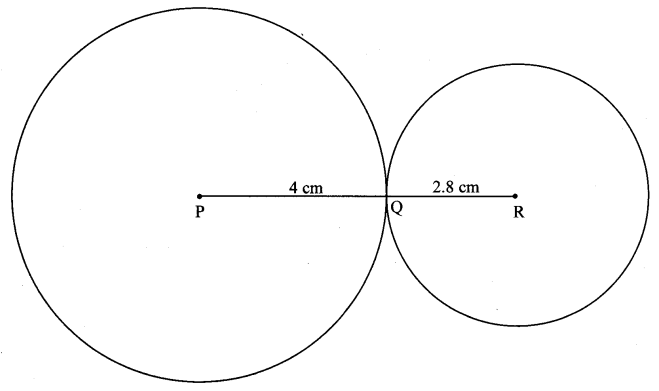
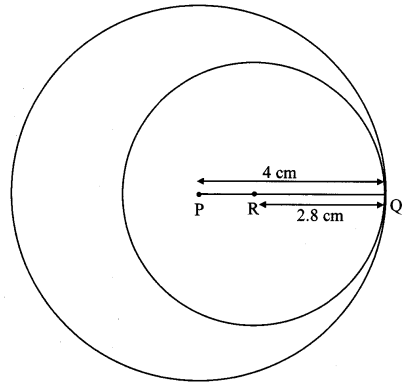
If radii of two circles are 4 cm and 2.8 cm. Draw figure of these circles touching each other
i. externally
ii. internally.
Solution:
i. Circles touching externally:
ii. Circles touching internally:
Question 4.
In the adjoining figure, the circles with centres P and Q touch each other at R A line passing through R meets the circles at A and B respectively. Prove that –
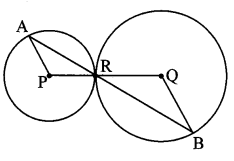
i. seg AP || seg BQ,
ii. ∆APR ~ ∆RQB, and
iii. Find ∠RQB if ∠PAR = 35°.
Solution:
The circles with centres P and Q touch each other at R.
∴ By theorem of touching circles,
P – R – Q
i. In ∆PAR,
seg PA = seg PR [Radii of the same circle]
∴ ∠PRA ≅ ∠PAR (i) [Isosceles triangle theorem]
Similarly, in ∆QBR,
seg QR = seg QB [Radii of the same circle]
∴ ∠RBQ ≅ ∠QRB (ii) [Isosceles triangle theorem]
But, ∠PRA ≅ ∠QRB (iii) [Vertically opposite angles]
∴ ∠PAR ≅ ∠RBQ (iv) [From (i) and (ii)]
But, they are a pair of alternate angles formed by transversal AB on seg AP and seg BQ.
∴ seg AP || seg BQ [Alternate angles test]
ii. In ∆APR and ∆RQB,
∠PAR ≅ ∠QRB [From (i) and (iii)]
∠APR ≅ ∠RQB [Alternate angles]
∴ ∆APR – ∆RQB [AA test of similarity]
iii. ∠PAR = 35° [Given]
∴ ∠RBQ = ∠PAR= 35° [From (iv)]
In ∆RQB,
∠RQB + ∠RBQ + ∠QRB = 180° [Sum of the measures of angles of a triangle is 180°]
∴ ∠RQB + ∠RBQ + ∠RBQ = 180° [From (ii)]
∴ ∠RQB + 2 ∠RBQ = 180°
∴ ∠RQB + 2 × 35° = 180°
∴ ∠RQB + 70° = 180°
∴ ∠RQB = 110°
Question 5.
In the adjoining figure, the circles with centres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD if the radii of the circles are 4 cm, 6 cm.
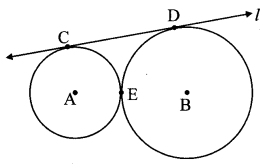
Construction : Draw seg AF ⊥ seg BD.
Solution:
i. The circles with centres A and B touch each other at E. [Given]
∴ By theorem of touching circles,
A – E – B
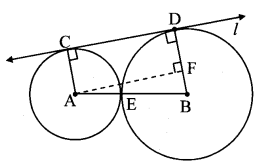
∴ ∠ACD = ∠BDC = 90° [Tangent theorem]
∠AFD = 90° [Construction]
∴ ∠CAF = 90° [Remaining angle of ꠸AFDC]
∴ ꠸AFDC is a rectangle. [Each angle is of measure 900]
∴ AC = DF = 4 cm [Opposite sides of a rectangle]
Now, BD = BF + DF [B – F – C]
∴ 6 = BF + 4 BF = 2 cm
Also, AB = AE + EB
= 4 + 6 = 10 cm
[The distance between the centres of circles touching externally is equal to the sum of their radii]
ii. Now, in ∆AFB, ∠AFB = 90° [Construction]
∴ AB2 = AF2 + BF2 [Pythagoras theorem]
∴ 102 = AF2 + 22
∴ 100 = AF2 + 4
∴ AF2 = 96
∴ AF = \(\sqrt { 96 }\) [Taking square root of both sides]
= \(\sqrt{16 \times 6}\)
= 4 \(\sqrt { 6 }\) cm
But, CD = AF [Opposite sides of a rectangle]
∴ CD = 4 \(\sqrt { 6 }\) cm
Question 1.
Take three collinear points X – Y – Z as shown in figure.
Draw a circle with centre X and radius XY. Draw another circle with centre Z and radius YZ.
Note that both the circles intersect each other at the single point Y. Draw a line / through point Y and perpendicular to seg XZ. What is line l (Textbook pg. no. 56)
Solution:
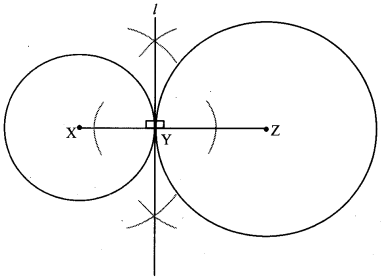
Line l is a common tangent of the two circles.
Question 2.
Take points Y – X – Z as shown in the figure. Draw a circle with centre Z and radius ZY.
Also draw a circle with centre X and radius XY. Note that both the circles intersect each other at the point Y.
Draw a line l perpendicular to seg YZ through point Y. What is line l? (Textbook pg. no. 56)
Solution:
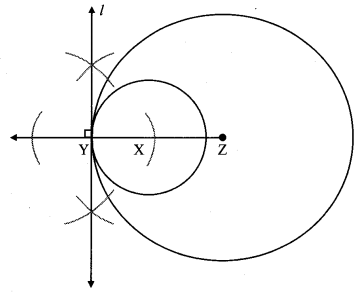
Line l is a common tangent of the two circles.
If two circles in the same plane intersect with a line in the plane in only one point, they are said to be touching circles and the line is their common tangent.
The point common to the circles and the line is called their common point of contact.
1. Circles touching externally:
For circles touching externally, the distance between their centres is equal to sum of their radii, i.e. AB = AC + BC
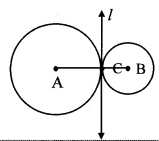
2. Circles touching internally:
For circles touching internally, the distance between their centres is equal to difference of their radii,
i. e. AB = AC – BC
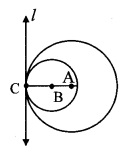
Question 3.
The circles shown in the given figure are called externally touching circles. Why? (iexthook pg. no. 57)
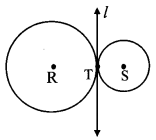
Answer:
Circles with centres R and S lie in the same plane and intersect with a line l in the plane in one and only one point T [R – T – S].
Hence the given circles are externally touching circles.
Question 4.
The circles shown in the given figure are called internally touching circles, why? (Textbook pg. no. 57)
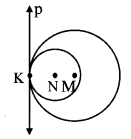
Answer:
Circles with centres N and M lie in the same plane and intersect with a line p in the plane in one and only one point T [K – N – M].
Hence, the given circles are internally touching circles.
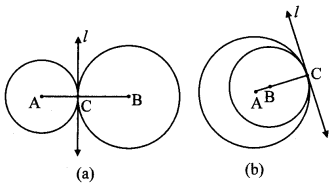
Question 5.
In the given figure, the radii of the circles with centres A and B are 3 cm and 4 cm respectively. Find
i. d(A,B) in figure (a)
ii. d(A,B) in figure (b) (Textbook pg. no. 57)
Solution:
i. Here, circle with centres A and B touch each other externally at point C.
∴ d(A, B) = d(A, C) + d(B ,C)
= 3 + 4
∴ d(A,B) = 7 cm
[The distance between the centres of circles touching externally is equal to the sum of their radii]
ii. Here, circle with centres A and 13 touch each other internally at point C.
∴ d(A, B) = d(A, C) – d(B, C)
= 4 – 3
∴ d(A,B) = 1 cm
[The distance between the centres of circles touching internally is equal to the difference in their radii]
covers the Practice Set 3.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 3 Circle.
Question 1.
Two circles having radii 3.5 cm and 4.8 cm touch each other internally. Find the distance between their centres.
Solution:
Let the two circles having centres P and Q touch each other internally at point R.
Here, QR = 3.5 cm, PR = 4.8 cm

The two circles touch each other internally.
∴ By theorem of touching circles,
P – Q – R
PQ = PR – QR
= 4.8 – 3.5
= 1.3 cm
[The distance between the centres of circles touching internally is equal to the difference in their radii]
Question 2.
Two circles of radii 5.5 cm and 4.2 cm touch each other externally. Find the distance between their centres.
Solution:
Let the two circles having centres P and R touch each other externally at point Q.
Here, PQ = 5.5 cm, QR = 4.2 cm
The two circles touch each other externally.
∴ By theorem of touching circles,
P – Q – R
PR = PQ + QR
= 5.5 + 4.2
= 9.7 cm
[The distance between the centres of the circles touching externally is equal to the sum of their radii]
Question 3.
If radii of two circles are 4 cm and 2.8 cm. Draw figure of these circles touching each other
i. externally
ii. internally.
Solution:
i. Circles touching externally:

ii. Circles touching internally:

Question 4.
In the adjoining figure, the circles with centres P and Q touch each other at R A line passing through R meets the circles at A and B respectively. Prove that –

i. seg AP || seg BQ,
ii. ∆APR ~ ∆RQB, and
iii. Find ∠RQB if ∠PAR = 35°.
Solution:
The circles with centres P and Q touch each other at R.
∴ By theorem of touching circles,
P – R – Q
i. In ∆PAR,
seg PA = seg PR [Radii of the same circle]
∴ ∠PRA ≅ ∠PAR (i) [Isosceles triangle theorem]
Similarly, in ∆QBR,
seg QR = seg QB [Radii of the same circle]
∴ ∠RBQ ≅ ∠QRB (ii) [Isosceles triangle theorem]
But, ∠PRA ≅ ∠QRB (iii) [Vertically opposite angles]
∴ ∠PAR ≅ ∠RBQ (iv) [From (i) and (ii)]
But, they are a pair of alternate angles formed by transversal AB on seg AP and seg BQ.
∴ seg AP || seg BQ [Alternate angles test]
ii. In ∆APR and ∆RQB,
∠PAR ≅ ∠QRB [From (i) and (iii)]
∠APR ≅ ∠RQB [Alternate angles]
∴ ∆APR – ∆RQB [AA test of similarity]
iii. ∠PAR = 35° [Given]
∴ ∠RBQ = ∠PAR= 35° [From (iv)]
In ∆RQB,
∠RQB + ∠RBQ + ∠QRB = 180° [Sum of the measures of angles of a triangle is 180°]
∴ ∠RQB + ∠RBQ + ∠RBQ = 180° [From (ii)]
∴ ∠RQB + 2 ∠RBQ = 180°
∴ ∠RQB + 2 × 35° = 180°
∴ ∠RQB + 70° = 180°
∴ ∠RQB = 110°
Question 5.
In the adjoining figure, the circles with centres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD if the radii of the circles are 4 cm, 6 cm.

Construction : Draw seg AF ⊥ seg BD.
Solution:
i. The circles with centres A and B touch each other at E. [Given]
∴ By theorem of touching circles,
A – E – B

∴ ∠ACD = ∠BDC = 90° [Tangent theorem]
∠AFD = 90° [Construction]
∴ ∠CAF = 90° [Remaining angle of ꠸AFDC]
∴ ꠸AFDC is a rectangle. [Each angle is of measure 900]
∴ AC = DF = 4 cm [Opposite sides of a rectangle]
Now, BD = BF + DF [B – F – C]
∴ 6 = BF + 4 BF = 2 cm
Also, AB = AE + EB
= 4 + 6 = 10 cm
[The distance between the centres of circles touching externally is equal to the sum of their radii]
ii. Now, in ∆AFB, ∠AFB = 90° [Construction]
∴ AB2 = AF2 + BF2 [Pythagoras theorem]
∴ 102 = AF2 + 22
∴ 100 = AF2 + 4
∴ AF2 = 96
∴ AF = \(\sqrt { 96 }\) [Taking square root of both sides]
= \(\sqrt{16 \times 6}\)
= 4 \(\sqrt { 6 }\) cm
But, CD = AF [Opposite sides of a rectangle]
∴ CD = 4 \(\sqrt { 6 }\) cm
Question 1.
Take three collinear points X – Y – Z as shown in figure.
Draw a circle with centre X and radius XY. Draw another circle with centre Z and radius YZ.
Note that both the circles intersect each other at the single point Y. Draw a line / through point Y and perpendicular to seg XZ. What is line l (Textbook pg. no. 56)
Solution:

Line l is a common tangent of the two circles.
Question 2.
Take points Y – X – Z as shown in the figure. Draw a circle with centre Z and radius ZY.
Also draw a circle with centre X and radius XY. Note that both the circles intersect each other at the point Y.
Draw a line l perpendicular to seg YZ through point Y. What is line l? (Textbook pg. no. 56)
Solution:

Line l is a common tangent of the two circles.
If two circles in the same plane intersect with a line in the plane in only one point, they are said to be touching circles and the line is their common tangent.
The point common to the circles and the line is called their common point of contact.
1. Circles touching externally:
For circles touching externally, the distance between their centres is equal to sum of their radii, i.e. AB = AC + BC

2. Circles touching internally:
For circles touching internally, the distance between their centres is equal to difference of their radii,
i. e. AB = AC – BC

Question 3.
The circles shown in the given figure are called externally touching circles. Why? (iexthook pg. no. 57)

Answer:
Circles with centres R and S lie in the same plane and intersect with a line l in the plane in one and only one point T [R – T – S].
Hence the given circles are externally touching circles.
Question 4.
The circles shown in the given figure are called internally touching circles, why? (Textbook pg. no. 57)

Answer:
Circles with centres N and M lie in the same plane and intersect with a line p in the plane in one and only one point T [K – N – M].
Hence, the given circles are internally touching circles.
Question 5.
In the given figure, the radii of the circles with centres A and B are 3 cm and 4 cm respectively. Find
i. d(A,B) in figure (a)
ii. d(A,B) in figure (b) (Textbook pg. no. 57)

Solution:
i. Here, circle with centres A and B touch each other externally at point C.
∴ d(A, B) = d(A, C) + d(B ,C)
= 3 + 4
∴ d(A,B) = 7 cm
[The distance between the centres of circles touching externally is equal to the sum of their radii]
ii. Here, circle with centres A and 13 touch each other internally at point C.
∴ d(A, B) = d(A, C) – d(B, C)
= 4 – 3
∴ d(A,B) = 1 cm
[The distance between the centres of circles touching internally is equal to the difference in their radii]