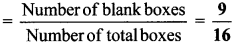Balbharti Maharashtra State Board Class 6 Maths Solutions
covers the Std 6 Maths Chapter 11 Ratio-Proportion Class 6 Practice Set 28 Answers Solutions.
6th Standard Maths Practice Set 28 Question 1.
In each example below, find the ratio of the first number to the second:
i. 24, 56
ii. 63,49
iii. 52, 65
iv. 84, 60
v. 35, 65
vi. 121, 99
Solution:
i. 24, 56
\(\frac{24}{56}=\frac{24 \div 8}{56 \div 8}=\frac{3}{7}\)
= 3:7
ii. 63,49
\(\frac{63}{49}=\frac{63 \div 7}{49 \div 7}=\frac{9}{7}\)
= 9:7
iii. 52, 65
\(\frac{52}{65}=\frac{52 \div 13}{65 \div 13}=\frac{4}{5}\)
= 4:5
iv. 84, 60
\(\frac{84}{60}=\frac{84 \div 12}{60 \div 12}=\frac{7}{5}\)
= 7:5
v. 35, 65
\(\frac{35}{65}=\frac{35 \div 5}{65 \div 5}=\frac{7}{13}\)
= 7:13
vi. 121, 99
\(\frac{121}{99}=\frac{121 \div 11}{99 \div 11}=\frac{11}{9}\)
= 11:9
6th Maths Practice Set 28 Question 2.
Find the ratio of the first quantity to the second.
i. 25 beads, 40 beads
ii. Rs 40, Rs 120
iii. 15 minutes, 1 hour
iv. 30 litres, 24 litres
v. 99 kg, 44000 grams
vi. 1 litre, 250 ml
vii. 60 paise, 1 rupee
viii. 750 grams, \(\frac { 1 }{ 2 }\) kg
ix. 125 cm, 1 metre
Solution:
i. Required Ratio = \(\frac{25}{40}=\frac{25 \div 5}{40 \div 5}=\frac{5}{8}\)
ii. Required Ratio = \(\frac{40}{120}=\frac{40 \div 40}{120 \div 40}=\frac{1}{3}\)
iii. 1 hour = 60 minutes
Required Ratio = \(\frac{15}{60}=\frac{15 \div 15}{60 \div 15}=\frac{1}{4}\)
iv. Required Ratio = \(\frac{30}{24}=\frac{30 \div 6}{24 \div 6}=\frac{5}{4}\)
v. 99 kg = 99 x 1000 grams = 99000 grams
Required Ratio = \(\frac{99000}{44000}=\frac{99000 \div 1000}{44000 \div 1000}=\frac{99}{44}\)
= \(\frac{99}{44}=\frac{99 \div 11}{44 \div 11}=\frac{9}{4}\)
vi. 1 litre, 250 ml
1 litre = 1000 ml
Required Ratio = \(\frac{1000}{250}=\frac{1000 \div 10}{250 \div 10}=\frac{100}{25}\)
= \(\frac{100}{25}=\frac{100 \div 25}{25 \div 25}=\frac{4}{1}\)
viii. 750 grams, \(\frac { 1 }{ 2 }\) kg
\(\frac { 1 }{ 2 }\) kg = \(\frac { 1000 }{ 2 }\) grams = 500 grams
Required Ratio = \(\frac{750}{500}=\frac{750 \div 10}{500 \div 10}=\frac{75}{50}\)
= \(\frac{75}{50}=\frac{75 \div 25}{50 \div 25}=\frac{3}{2}\)
ix. 125 cm, 1 metre
1 metre = 100 cm
Required Ratio = \(\frac{125}{100}=\frac{125 \div 25}{100 \div 25}=\frac{5}{4}\)
6th Std Maths Practice Set 28 Question 3.
Reema has 24 notebooks and 18 books. Find the ratio of notebooks to books.
Solution:
Ratio of notebooks to books
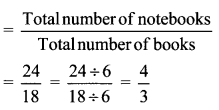
∴ The ratio of notebooks to books with Reema is \(\frac { 4 }{ 3 }\)
Practice Set 28 Question 4.
30 cricket players and 20 kho-kho players are training on a field. What is the ratio of cricket players to the total number of players?
Solution:
Total number of players = Cricket players + Kho-kho players
= 30 + 20 = 50
Ratio of cricket players to the total number of players
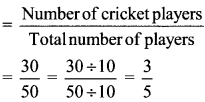
∴ The ratio of cricket players to the total number of players is \(\frac { 3 }{ 5 }\).
Question 5.
Snehal has a red ribbon that is 80 cm long and a blue ribbon 2.20 m long. What is the ratio of the length of the red ribbon to that of the blue ribbon?
Solution:
1 metre =100 cm
Length of the red ribbon = 80 cm
Length of the blue ribbon = 2.20 m = 2.20 x 100 cm
\(=\frac{220}{100} \times \frac{100}{1}=\frac{220 \times 100}{100 \times 1}\)
= 220 cm
∴ Ratio of length of the red ribbon to that of the blue ribbon

∴ The ratio of the length of the red ribbon to that of the blue ribbon is \(\frac { 4 }{ 11 }\).
11 Ratio Question 6.
Shubham’s age today is 12 years and his father’s is 42 years. Shubham’s mother is younger than his father by 6 years. Find the following ratios.
i. Ratio of Shubham’s age today to his mother’s age today.
ii. Ratio of Shubham’s mother’s age today to his father’s age today.
iii. The ratio of Shubham’s age to his mother’s age when Shubham was 10 years old.
Solution:
Shubham’s age today = 12 years
Shubham’s father’s age = 42 years
Shubham’s mother age = Shubham’s father’s age – 6 years
= 42 years – 6 years = 36 years
i. Ratio of Shubham’s age today to his mother’s age today

∴ The ratio of Shubham’s age today to his mother’s age today is \(\frac { 1 }{ 3 }\).
ii. Ratio of Shubham’s mother age today to his father’s age today

∴ The ratio of Shubham’s mother’s age today to his father’s age today is \(\frac { 6 }{ 7 }\).
iii. Shubham’s age today is 12 years and his mothers age is 36 years.
Hence when Shubham’s age was 10 years, his mother’s age was 34 years (i.e. 36 – 2 years).
Ratio of Shubham’s age to his mother’s age when Shubham was 10 years old
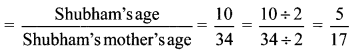
∴ The ratio of Shubham’s age to his mother’s age when Shubham was 10 years old is \(\frac { 5 }{ 17 }\)
Question 1.
In the figure, colour some squares with any colour you like and leave some blank. (Textbook pg. no. 57)

i. Count all the boxes and write the number.
ii. Count the colored ones and write the number.
iii. Count the blank ones and write the number.
iv. Find the ratio of the colored boxes to the blank ones.
v. Find the ratio of the colored boxes to the total boxes.
vi. Find the ratio of the blank boxes to the total boxes.
Solution:
i. The number of all boxes is 16.
ii. The number of colored boxes is 7.
iii. The number of blank boxes is 9.
iv. Ratio of the colored boxes to the blank ones

v. Ratio of the colored boxes to the total boxes
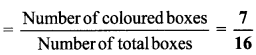
vi. Ratio of the blank boxes to the total boxes
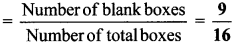
covers the Std 6 Maths Chapter 11 Ratio-Proportion Class 6 Practice Set 28 Answers Solutions.
6th Standard Maths Practice Set 28 Question 1.
In each example below, find the ratio of the first number to the second:
i. 24, 56
ii. 63,49
iii. 52, 65
iv. 84, 60
v. 35, 65
vi. 121, 99
Solution:
i. 24, 56
\(\frac{24}{56}=\frac{24 \div 8}{56 \div 8}=\frac{3}{7}\)
= 3:7
ii. 63,49
\(\frac{63}{49}=\frac{63 \div 7}{49 \div 7}=\frac{9}{7}\)
= 9:7
iii. 52, 65
\(\frac{52}{65}=\frac{52 \div 13}{65 \div 13}=\frac{4}{5}\)
= 4:5
iv. 84, 60
\(\frac{84}{60}=\frac{84 \div 12}{60 \div 12}=\frac{7}{5}\)
= 7:5
v. 35, 65
\(\frac{35}{65}=\frac{35 \div 5}{65 \div 5}=\frac{7}{13}\)
= 7:13
vi. 121, 99
\(\frac{121}{99}=\frac{121 \div 11}{99 \div 11}=\frac{11}{9}\)
= 11:9
6th Maths Practice Set 28 Question 2.
Find the ratio of the first quantity to the second.
i. 25 beads, 40 beads
ii. Rs 40, Rs 120
iii. 15 minutes, 1 hour
iv. 30 litres, 24 litres
v. 99 kg, 44000 grams
vi. 1 litre, 250 ml
vii. 60 paise, 1 rupee
viii. 750 grams, \(\frac { 1 }{ 2 }\) kg
ix. 125 cm, 1 metre
Solution:
i. Required Ratio = \(\frac{25}{40}=\frac{25 \div 5}{40 \div 5}=\frac{5}{8}\)
ii. Required Ratio = \(\frac{40}{120}=\frac{40 \div 40}{120 \div 40}=\frac{1}{3}\)
iii. 1 hour = 60 minutes
Required Ratio = \(\frac{15}{60}=\frac{15 \div 15}{60 \div 15}=\frac{1}{4}\)
iv. Required Ratio = \(\frac{30}{24}=\frac{30 \div 6}{24 \div 6}=\frac{5}{4}\)
v. 99 kg = 99 x 1000 grams = 99000 grams
Required Ratio = \(\frac{99000}{44000}=\frac{99000 \div 1000}{44000 \div 1000}=\frac{99}{44}\)
= \(\frac{99}{44}=\frac{99 \div 11}{44 \div 11}=\frac{9}{4}\)
vi. 1 litre, 250 ml
1 litre = 1000 ml
Required Ratio = \(\frac{1000}{250}=\frac{1000 \div 10}{250 \div 10}=\frac{100}{25}\)
= \(\frac{100}{25}=\frac{100 \div 25}{25 \div 25}=\frac{4}{1}\)
viii. 750 grams, \(\frac { 1 }{ 2 }\) kg
\(\frac { 1 }{ 2 }\) kg = \(\frac { 1000 }{ 2 }\) grams = 500 grams
Required Ratio = \(\frac{750}{500}=\frac{750 \div 10}{500 \div 10}=\frac{75}{50}\)
= \(\frac{75}{50}=\frac{75 \div 25}{50 \div 25}=\frac{3}{2}\)
ix. 125 cm, 1 metre
1 metre = 100 cm
Required Ratio = \(\frac{125}{100}=\frac{125 \div 25}{100 \div 25}=\frac{5}{4}\)
6th Std Maths Practice Set 28 Question 3.
Reema has 24 notebooks and 18 books. Find the ratio of notebooks to books.
Solution:
Ratio of notebooks to books
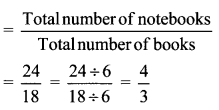
∴ The ratio of notebooks to books with Reema is \(\frac { 4 }{ 3 }\)
Practice Set 28 Question 4.
30 cricket players and 20 kho-kho players are training on a field. What is the ratio of cricket players to the total number of players?
Solution:
Total number of players = Cricket players + Kho-kho players
= 30 + 20 = 50
Ratio of cricket players to the total number of players
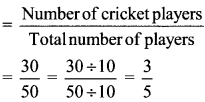
∴ The ratio of cricket players to the total number of players is \(\frac { 3 }{ 5 }\).
Question 5.
Snehal has a red ribbon that is 80 cm long and a blue ribbon 2.20 m long. What is the ratio of the length of the red ribbon to that of the blue ribbon?
Solution:
1 metre =100 cm
Length of the red ribbon = 80 cm
Length of the blue ribbon = 2.20 m = 2.20 x 100 cm
\(=\frac{220}{100} \times \frac{100}{1}=\frac{220 \times 100}{100 \times 1}\)
= 220 cm
∴ Ratio of length of the red ribbon to that of the blue ribbon

∴ The ratio of the length of the red ribbon to that of the blue ribbon is \(\frac { 4 }{ 11 }\).
11 Ratio Question 6.
Shubham’s age today is 12 years and his father’s is 42 years. Shubham’s mother is younger than his father by 6 years. Find the following ratios.
i. Ratio of Shubham’s age today to his mother’s age today.
ii. Ratio of Shubham’s mother’s age today to his father’s age today.
iii. The ratio of Shubham’s age to his mother’s age when Shubham was 10 years old.
Solution:
Shubham’s age today = 12 years
Shubham’s father’s age = 42 years
Shubham’s mother age = Shubham’s father’s age – 6 years
= 42 years – 6 years = 36 years
i. Ratio of Shubham’s age today to his mother’s age today

∴ The ratio of Shubham’s age today to his mother’s age today is \(\frac { 1 }{ 3 }\).
ii. Ratio of Shubham’s mother age today to his father’s age today

∴ The ratio of Shubham’s mother’s age today to his father’s age today is \(\frac { 6 }{ 7 }\).
iii. Shubham’s age today is 12 years and his mothers age is 36 years.
Hence when Shubham’s age was 10 years, his mother’s age was 34 years (i.e. 36 – 2 years).
Ratio of Shubham’s age to his mother’s age when Shubham was 10 years old
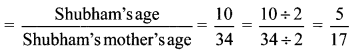
∴ The ratio of Shubham’s age to his mother’s age when Shubham was 10 years old is \(\frac { 5 }{ 17 }\)
Question 1.
In the figure, colour some squares with any colour you like and leave some blank. (Textbook pg. no. 57)

i. Count all the boxes and write the number.
ii. Count the colored ones and write the number.
iii. Count the blank ones and write the number.
iv. Find the ratio of the colored boxes to the blank ones.
v. Find the ratio of the colored boxes to the total boxes.
vi. Find the ratio of the blank boxes to the total boxes.
Solution:
i. The number of all boxes is 16.
ii. The number of colored boxes is 7.
iii. The number of blank boxes is 9.
iv. Ratio of the colored boxes to the blank ones

v. Ratio of the colored boxes to the total boxes
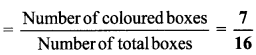
vi. Ratio of the blank boxes to the total boxes