Balbharti Maharashtra State Board Class 8 Maths Solutions
covers the Practice Set 4.1 8th Std Maths Answers Solutions Chapter 4 Altitudes and Medians of a Triangle.
Question 1.
In ∆LMN, ___ is an altitude and __ is a median, (write the names of appropriate segments.)
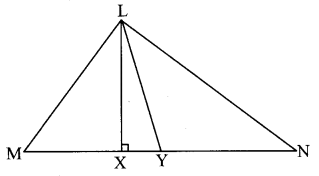
Solution:
In ∆LMN, seg LX is an altitude and seg LY is a median.
Question 2.
Draw an acute angled ∆PQR. Draw all of its altitudes. Name the point of concurrence as ‘O’.
Solution:
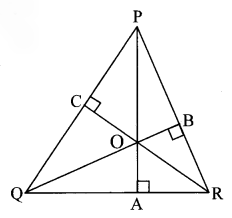
Question 3.
Draw an obtuse angled ∆STV. Draw its medians and show the centroid.
Solution:
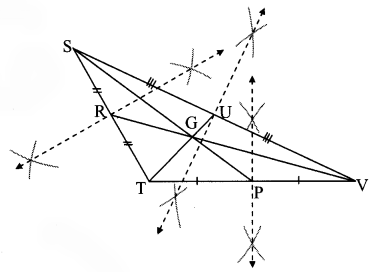
Question 4.
Draw an obtuse angled ∆LMN. Draw its altitudes and denote the ortho centre by ‘O’.
Solution:
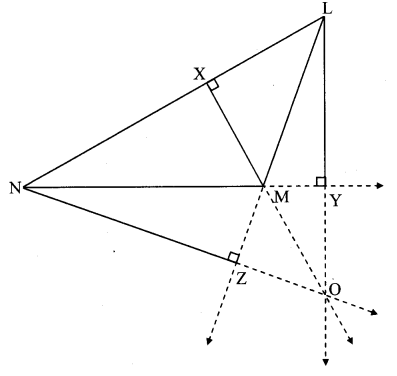
Question 5.
Draw a right angled ∆XYZ. Draw its medians and show their point of concurrence by G.
Solution:
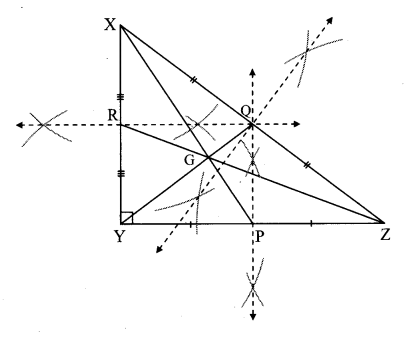
Question 6.
Draw an isosceles triangle. Draw all of its medians and altitudes. Write your observation about their points of concurrence.
Solution:
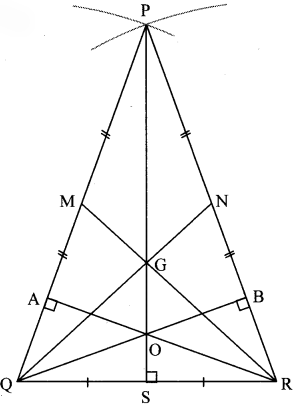
The point of concurrence of medians i.e. G and that of altitudes i.e. O lie on the same line PS which is the perpendicular bisector of seg QR.
Question 7.
Fill in the blanks.
Point G is the centroid of ∆ABC.
i. If l(RG) = 2.5, then l(GC) = ___
ii. If l(BG) = 6, then l(BQ) = ____
iii. If l(AP) = 6, then l(AG) = ___ and l(GP) = ___.
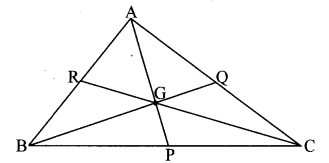
Solution:
The centroid of a triangle divides each median in the ratio 2:1.
i. Point G is the centroid and seg CR is the median.
∴ \(\frac{l(\mathrm{GC})}{l(\mathrm{RG})}=\frac{2}{1}\)
∴ \(\frac{l(\mathrm{GC})}{2.5}=\frac{2}{1}\) ……[∵ l(RG) = 2.5]
∴ l(GC) × 1 = 2 × 2.5
∴ l(GC) = 5
ii. Point G is the centroid and seg BQ is the median.
∴ \(\frac{l(\mathrm{BG})}{l(\mathrm{GQ})}=\frac{2}{1}\)
∴ \(\frac{6}{l(\mathrm{GQ})}=\frac{2}{1}\) …..[∵ l(BG) = 6]
∴ 6 × 1 = 2 × l(GQ)
∴ \(\frac { 6 }{ 2 }\) = l(GQ)
∴ 3 = l(GQ)
i.e. l(GQ) = 3
Now, l (BQ) = l(BG) + l(GQ)
∴ l(BQ) = 6 + 3
∴ l(BQ) = 9
iii. Point G is the centroid and seg AP is the median.
∴ \(\frac{l(\mathrm{AG})}{l(\mathrm{GP})}=\frac{2}{1}\)
∴ l(AG) = 2 l(GP) …..(i)
Now, l(AP) = l(AG) + l(GP) … (ii)
∴ l(AP) = 2l(GP) + l(GP) … [From (i)]
∴ l(AP) = 3l(GP)
∴ 6 = 3l(GP) ..[∵ l(AP) = 6]
∴ \(\frac { 6 }{ 3 }\) = l(GP)
∴ 2 = l(GP)
i.e. l(GP) = 2
l(AP) = l(AG) + l(GP) …[from (ii)]
∴ 6 = l(AG) + 2
∴ l(AG) = 6 – 2
∴ l(AG) = 4
Maharashtra Board Class 8 Maths Chapter 4 Altitudes and Medians of a Triangle Practice Set 4.1 Intext Questions and Activities
Question 1.
Draw a line. Take a point outside the line. Draw a perpendicular from the point to the line with the help of a set-square (Textbook pg. no, 19)
Solution:
Step 1: Draw a line l and a point P lying outside it.

Step 2: By placing a set-square on line l, draw a perpendicular to the line from point P.
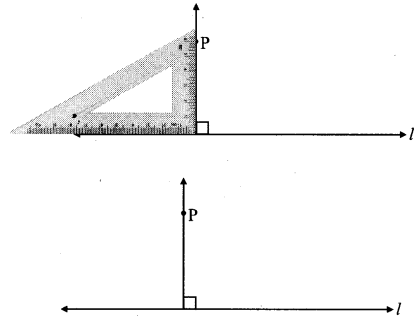
Question 2.
Draw an acute angled ∆ABC and all its altitudes. Observe the location of the orthocentre. (Textbook pg. no. 20)
Solution:
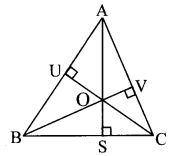
Point O is the orthocentre.
Orthocentre lies in the interior of ∆ABC.
Question 3.
Draw a right angled triangle and draw all its altitudes. Write the point of concurrence. (Textbook: pg, no. 20)
Solution:
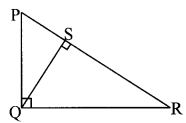
Point Q is the orthocentre.
The point of concurrence of altitudes PQ, QR and QS is Q.
Question 4.
i. Draw an obtuse angled triangle and all its altitudes.
ii. Do they intersect each other?
Draw the lines containing the altitudes. Observe that these lines are concurrent. (Textbook pg. no. 20)
Solution:
i.
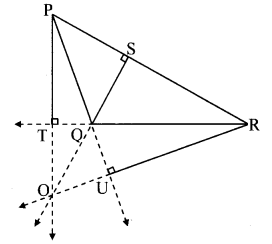
Point O is the orthocentre.
ii. Yes, all the altitudes intersect at point O in the exterior of ∆PQR.
Question 5.
Draw three different triangles; a right angled triangle, an obtuse angled triangle and an acute angled triangle. Draw the medians of the triangles. Note that the centroid of each of them is in the interior of the triangle. (Textbook pg. no. 21)
Solution:
i. Right angled triangle:
ii. Obtuse angled triangle:
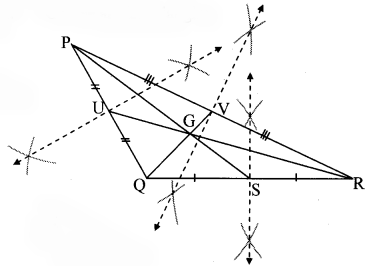
iii. Acute angled triangle:
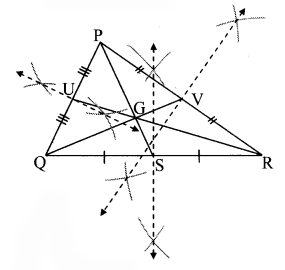
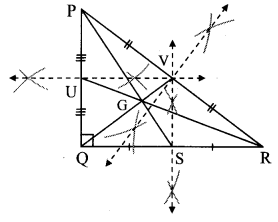
Question 6.
Draw a sufficiently large ∆ABC.
Draw medians; seg AR, seg BQ and seg CP of ∆ABC.
Name the point of concurrence as G.
Measure the lengths of segments from the figure and fill in the boxes in the following table.
Observe that all of these ratios are nearly 2 : 1 (Textbook pg. no. 21)
Solution:
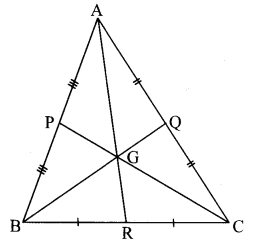
Question 7.
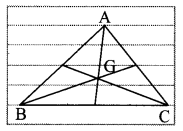
As shown in the given figure, a student drew ∆ABC using five parallel lines of a notebook. Then he found the centroid G of the triangle. How will you decide whether the location of G he found, is correct. (Textbook pg. no. 21)
Solution:
Draw seg AP ⊥ seg PE and seg EQ ⊥ seg QC.
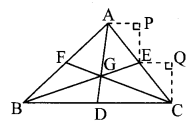
Side AP || side EQ and AC is their transversal.
∴ ∠PAE ≅ ∠QEC …(i) [Corresponding angles]
In ∆ APE and ∆ EQC,
∠PAE ≅ ∠QEC …[From (i)]
∠APE ≅ ∠EQC
… [Each angle is of measure 90°]
side PE ≅ side QC
…. [Perpendicular distance between parallel lines]
∴ ∆ APE ≅ ∆ EQC … [By AAS test]
∴ AE = EC
… [Corresponding sides of congruent triangles]
∴ E is the midpoint of AC.
∴ seg BE is the median.
Similarly, seg CF is the median.
Since, the medians of a triangle are concurrent.
∴ G is the centroid of ∆ABC.
Question 8.
Draw an equilateral triangle. Find its circumcentre (C), incentre (I), centroid (G) and orthocentre (O). Write your observation. (Textbook pg. no. 22)
Solution:
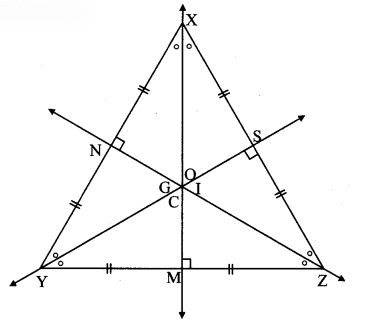
From the figure, circumcentre (C), incentre (I), centroid (G) and orthocentre (O) of an equilateral triangle are the same.
Question 9.
Draw an isosceles triangle. Locate its centroid, orthocentre, circumcentre and incentre. Verify that they are collinear. (Textbook pg. no. 22)
Solution:
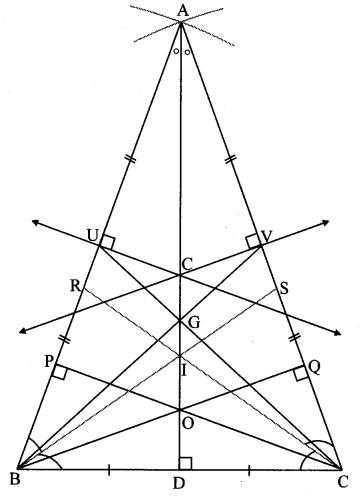
From the figure, centroid (G), orthocentre (O), circumcentre (C) and incentre (I) of an isosceles triangle lie on the same line AD.
∴ they are collinear.
covers the Practice Set 4.1 8th Std Maths Answers Solutions Chapter 4 Altitudes and Medians of a Triangle.
Question 1.
In ∆LMN, ___ is an altitude and __ is a median, (write the names of appropriate segments.)

Solution:
In ∆LMN, seg LX is an altitude and seg LY is a median.
Question 2.
Draw an acute angled ∆PQR. Draw all of its altitudes. Name the point of concurrence as ‘O’.
Solution:

Question 3.
Draw an obtuse angled ∆STV. Draw its medians and show the centroid.
Solution:

Question 4.
Draw an obtuse angled ∆LMN. Draw its altitudes and denote the ortho centre by ‘O’.
Solution:

Question 5.
Draw a right angled ∆XYZ. Draw its medians and show their point of concurrence by G.
Solution:

Question 6.
Draw an isosceles triangle. Draw all of its medians and altitudes. Write your observation about their points of concurrence.
Solution:

The point of concurrence of medians i.e. G and that of altitudes i.e. O lie on the same line PS which is the perpendicular bisector of seg QR.
Question 7.
Fill in the blanks.
Point G is the centroid of ∆ABC.
i. If l(RG) = 2.5, then l(GC) = ___
ii. If l(BG) = 6, then l(BQ) = ____
iii. If l(AP) = 6, then l(AG) = ___ and l(GP) = ___.

Solution:
The centroid of a triangle divides each median in the ratio 2:1.
i. Point G is the centroid and seg CR is the median.
∴ \(\frac{l(\mathrm{GC})}{l(\mathrm{RG})}=\frac{2}{1}\)
∴ \(\frac{l(\mathrm{GC})}{2.5}=\frac{2}{1}\) ……[∵ l(RG) = 2.5]
∴ l(GC) × 1 = 2 × 2.5
∴ l(GC) = 5
ii. Point G is the centroid and seg BQ is the median.
∴ \(\frac{l(\mathrm{BG})}{l(\mathrm{GQ})}=\frac{2}{1}\)
∴ \(\frac{6}{l(\mathrm{GQ})}=\frac{2}{1}\) …..[∵ l(BG) = 6]
∴ 6 × 1 = 2 × l(GQ)
∴ \(\frac { 6 }{ 2 }\) = l(GQ)
∴ 3 = l(GQ)
i.e. l(GQ) = 3
Now, l (BQ) = l(BG) + l(GQ)
∴ l(BQ) = 6 + 3
∴ l(BQ) = 9
iii. Point G is the centroid and seg AP is the median.
∴ \(\frac{l(\mathrm{AG})}{l(\mathrm{GP})}=\frac{2}{1}\)
∴ l(AG) = 2 l(GP) …..(i)
Now, l(AP) = l(AG) + l(GP) … (ii)
∴ l(AP) = 2l(GP) + l(GP) … [From (i)]
∴ l(AP) = 3l(GP)
∴ 6 = 3l(GP) ..[∵ l(AP) = 6]
∴ \(\frac { 6 }{ 3 }\) = l(GP)
∴ 2 = l(GP)
i.e. l(GP) = 2
l(AP) = l(AG) + l(GP) …[from (ii)]
∴ 6 = l(AG) + 2
∴ l(AG) = 6 – 2
∴ l(AG) = 4
Maharashtra Board Class 8 Maths Chapter 4 Altitudes and Medians of a Triangle Practice Set 4.1 Intext Questions and Activities
Question 1.
Draw a line. Take a point outside the line. Draw a perpendicular from the point to the line with the help of a set-square (Textbook pg. no, 19)
Solution:
Step 1: Draw a line l and a point P lying outside it.

Step 2: By placing a set-square on line l, draw a perpendicular to the line from point P.

Question 2.
Draw an acute angled ∆ABC and all its altitudes. Observe the location of the orthocentre. (Textbook pg. no. 20)
Solution:

Point O is the orthocentre.
Orthocentre lies in the interior of ∆ABC.
Question 3.
Draw a right angled triangle and draw all its altitudes. Write the point of concurrence. (Textbook: pg, no. 20)
Solution:

Point Q is the orthocentre.
The point of concurrence of altitudes PQ, QR and QS is Q.
Question 4.
i. Draw an obtuse angled triangle and all its altitudes.
ii. Do they intersect each other?
Draw the lines containing the altitudes. Observe that these lines are concurrent. (Textbook pg. no. 20)
Solution:
i.

Point O is the orthocentre.
ii. Yes, all the altitudes intersect at point O in the exterior of ∆PQR.
Question 5.
Draw three different triangles; a right angled triangle, an obtuse angled triangle and an acute angled triangle. Draw the medians of the triangles. Note that the centroid of each of them is in the interior of the triangle. (Textbook pg. no. 21)
Solution:
i. Right angled triangle:

ii. Obtuse angled triangle:

iii. Acute angled triangle:

Question 6.
Draw a sufficiently large ∆ABC.
Draw medians; seg AR, seg BQ and seg CP of ∆ABC.
Name the point of concurrence as G.
Measure the lengths of segments from the figure and fill in the boxes in the following table.
| l(AG) = | l(GR) = | l(AG): l(GR) = |
| l(BG) = | l(GQ) = | l(BG): l(GQ) = |
| l(CG) = | l(GP) = | l(CG): l(GP) = |
Solution:

| l(AG) = 2.9 | l(GR) = 1.4 | l(AG): l(GR) = \(\frac{2.8}{1.4}=\frac{2}{1}\) |
| l(BG) = 2.4 | l(GQ) = 1.2 | l(BG): l(GQ) = \(\frac{2.4}{1.2}=\frac{2}{1}\) |
| l(CG) = 2.8 | l(GP) = 1.4 | l(CG): l(GP) = \(\frac{2.8}{1.4}=\frac{2}{1}\) |
As shown in the given figure, a student drew ∆ABC using five parallel lines of a notebook. Then he found the centroid G of the triangle. How will you decide whether the location of G he found, is correct. (Textbook pg. no. 21)

Solution:
Draw seg AP ⊥ seg PE and seg EQ ⊥ seg QC.

Side AP || side EQ and AC is their transversal.
∴ ∠PAE ≅ ∠QEC …(i) [Corresponding angles]
In ∆ APE and ∆ EQC,
∠PAE ≅ ∠QEC …[From (i)]
∠APE ≅ ∠EQC
… [Each angle is of measure 90°]
side PE ≅ side QC
…. [Perpendicular distance between parallel lines]
∴ ∆ APE ≅ ∆ EQC … [By AAS test]
∴ AE = EC
… [Corresponding sides of congruent triangles]
∴ E is the midpoint of AC.
∴ seg BE is the median.
Similarly, seg CF is the median.
Since, the medians of a triangle are concurrent.
∴ G is the centroid of ∆ABC.
Question 8.
Draw an equilateral triangle. Find its circumcentre (C), incentre (I), centroid (G) and orthocentre (O). Write your observation. (Textbook pg. no. 22)
Solution:

From the figure, circumcentre (C), incentre (I), centroid (G) and orthocentre (O) of an equilateral triangle are the same.
Question 9.
Draw an isosceles triangle. Locate its centroid, orthocentre, circumcentre and incentre. Verify that they are collinear. (Textbook pg. no. 22)
Solution:

From the figure, centroid (G), orthocentre (O), circumcentre (C) and incentre (I) of an isosceles triangle lie on the same line AD.
∴ they are collinear.