Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf
Chapter 4 Sequences and Series Ex 4.4 Questions and Answers.
Question 1.
Verify whether the following sequences are H.P.
(i) \(\frac{1}{3}, \frac{1}{5}, \frac{1}{7}, \frac{1}{9}, \ldots\)
(ii) \(\frac{1}{3}, \frac{1}{6}, \frac{1}{9}, \frac{1}{12}, \ldots \ldots \ldots \ldots\)
(iii) \(\frac{1}{7}, \frac{1}{9}, \frac{1}{11}, \frac{1}{13}, \frac{1}{15}, \ldots\)
Solution:
(i) \(\frac{1}{3}, \frac{1}{5}, \frac{1}{7}, \frac{1}{9}, \ldots\)
Here, the reciprocal sequence is 3, 5, 7, 9, …
∴ t1 = 3, t2 = 5, t3 = 7, …..
∵ t2 – t1 = t3 – t2 = t4 – t3 = 2, constant
∴ The reciprocal sequence is an A.P.
∴ the given sequence is H.P.
(ii) \(\frac{1}{3}, \frac{1}{6}, \frac{1}{9}, \frac{1}{12}, \ldots \ldots \ldots \ldots\)
Here, the reciprocal sequence is 3, 6, 9, 12 …
∴ t1 = 3, t2 = 6, t3 = 9, t4 = 12, …
∵ t2 – t1 = t3 – t2 = t4 – t3 = 3, constant
∴ The reciprocal sequence is an A.P.
∴ The given sequence is H.P.
(iii) \(\frac{1}{7}, \frac{1}{9}, \frac{1}{11}, \frac{1}{13}, \frac{1}{15}, \ldots\)
Here, the reciprocal sequence is 7, 9, 11, 13, 15, ……
∴ t1 = 7, t2 = 9, t3 = 11, t4 = 13, …..
∵ t2 – t1 = t3 – t2 = t4 – t3 = 2, constant
∴ The reciprocal sequence is an A.P.
∴ The given sequence is H.P.

Question 2.
Find the nth term and hence find the 8th term of the following H.P.s:
(i) \(\frac{1}{2}, \frac{1}{5}, \frac{1}{8}, \frac{1}{11}, \ldots \ldots \ldots\)
(ii) \(\frac{1}{4}, \frac{1}{6}, \frac{1}{8}, \frac{1}{10}, \ldots \ldots \ldots \ldots\)
(iii) \(\frac{1}{5}, \frac{1}{10}, \frac{1}{15}, \frac{1}{20}, \cdots \cdots \cdots\)
Solution:


Question 3.
Find A.M. of two positive numbers whose G.M. and H.M. are 4 and \(\frac{16}{5}\).
Solution:
G.M. = 4, H.M. = \(\frac{16}{5}\)
∵ (G.M.)2 = (A.M.) (H.M.)
∴ 16 = A.M. × \(\frac{16}{5}\)
∴ A.M. = 5
Question 4.
Find H.M. of two positive numbers whose A.M. and G.M. are \(\frac{15}{2}\) and 6.
Solution:
A.M. = \(\frac{15}{2}\), G.M. = 6
Now, (G.M.)2 = (A.M.) (H.M.)
∴ 62 = \(\frac{15}{2}\) × H.M.
∴ H.M. = 36 × \(\frac{2}{15}\)
∴ H.M. = \(\frac{24}{5}\)
Question 5.
Find G.M. of two positive numbers whose A.M. and H.M. are 75 and 48.
Solution:
A.M. = 75, H.M. = 48
(G.M.)2 = (A.M.) (H.M.)
∵ (G.M.)2 = 75 × 48
∵ (G.M.)2 = 25 × 3 × 16 × 3
∵ (G.M.)2 = 52 × 42 × 32
∴ G.M. = 5 × 4 × 3
∴ G.M. = 60

Question 6.
Insert two numbers between \(\frac{1}{7}\) and \(\frac{1}{13}\) so that the resulting sequence is a H.P.
Solution:
Let the required numbers be \(\frac{1}{\mathrm{H}_{1}}\) and \(\frac{1}{\mathrm{H}_{2}}\).
∴ \(\frac{1}{7}, \frac{1}{\mathrm{H}_{1}}, \frac{1}{\mathrm{H}_{2}}, \frac{1}{13}\) are in H.P.
∴ 7, H1, H2 and 13 are in A.P.
∴ t1 = a = 7 and t4 = a + 3d = 13
∴ 7 + 3d = 13
∴ 3d = 6
∴ d = 2
∴ H1 = t2 = a + d = 7 + 2 = 9
and H2 = t3 = a + 2d = 7 + 2(2) = 11
∴ \(\frac{1}{9}\) and \(\frac{1}{11}\) are the required numbers to be inserted between \(\frac{1}{7}\) and \(\frac{1}{13}\) so that the resulting sequence is a H.P.
Question 7.
Insert two numbers between 1 and -27 so that the resulting sequence is a G.P.
Solution:
Let the required numbers be G1 and G2.
∴ 1, G1, G2, -27 are in G.P.
∴ t1 = 1, t2 = G1, t3 = G2, t4 = -27
∴ t1 = a = 1
tn = arn-1
∴ t4 = (1) r4-1
∴ -27 = r3
∴ r3 = (-3)3
∴ r = -3
∴ G1 = t2 = ar = 1(-3) = -3
∴ G2 = t3 = ar = 1(-3)2 = 9
∴ -3 and 9 are the required numbers to be inserted between 1 and -27 so that the resulting sequence is a G.P.
Question 8.
Find two numbers whose A.M. exceeds their G.M. by \(\frac{1}{2}\) and their H.M. by \(\frac{25}{26}\).
Solution:
Let a, b be the two numbers.
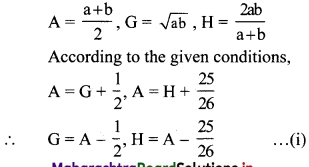

∴ a + b = 13
∴ b = 13 – a …….(iii)
and ab = 36
∴ a(13 – a) = 36 …… [From (iii)]
∴ a2 – 13a + 36 = 0
∴ (a – 4)(a – 9) = 0
∴ a = 4 or a = 9
When a = 4, b = 13 – 4 = 9
When a = 9, b = 13 – 9 = 4
∴ the two numbers are 4 and 9.

Question 9.
Find two numbers whose A.M. exceeds G.M. bv 7 and their H.M. by \(\frac{63}{5}\).
Solution:
Let a, b be the two numbers.

∴ a + b = 70
∴ b = 70 – a …..(ii)
∴ G = A – 7 = 35 – 7 = 28 …….[From (i)]
∴ √ab = 28
∴ ab = 282 = 784
∴ a(70 – a) = 784 ……[From (ii)]
∴ 70a – a2 = 784
∴ a2 – 70a + 784 = 0
∴ a2 – 56a – 14a + 784 = 0
∴ (a – 56) (a – 14) = 0
∴ a = 14 or a = 56
When a = 14, b = 70 – 14 = 56
When a = 56, b = 70 – 56 = 14
∴ the two numbers are 14 and 56.
Chapter 4 Sequences and Series Ex 4.4 Questions and Answers.
Question 1.
Verify whether the following sequences are H.P.
(i) \(\frac{1}{3}, \frac{1}{5}, \frac{1}{7}, \frac{1}{9}, \ldots\)
(ii) \(\frac{1}{3}, \frac{1}{6}, \frac{1}{9}, \frac{1}{12}, \ldots \ldots \ldots \ldots\)
(iii) \(\frac{1}{7}, \frac{1}{9}, \frac{1}{11}, \frac{1}{13}, \frac{1}{15}, \ldots\)
Solution:
(i) \(\frac{1}{3}, \frac{1}{5}, \frac{1}{7}, \frac{1}{9}, \ldots\)
Here, the reciprocal sequence is 3, 5, 7, 9, …
∴ t1 = 3, t2 = 5, t3 = 7, …..
∵ t2 – t1 = t3 – t2 = t4 – t3 = 2, constant
∴ The reciprocal sequence is an A.P.
∴ the given sequence is H.P.
(ii) \(\frac{1}{3}, \frac{1}{6}, \frac{1}{9}, \frac{1}{12}, \ldots \ldots \ldots \ldots\)
Here, the reciprocal sequence is 3, 6, 9, 12 …
∴ t1 = 3, t2 = 6, t3 = 9, t4 = 12, …
∵ t2 – t1 = t3 – t2 = t4 – t3 = 3, constant
∴ The reciprocal sequence is an A.P.
∴ The given sequence is H.P.
(iii) \(\frac{1}{7}, \frac{1}{9}, \frac{1}{11}, \frac{1}{13}, \frac{1}{15}, \ldots\)
Here, the reciprocal sequence is 7, 9, 11, 13, 15, ……
∴ t1 = 7, t2 = 9, t3 = 11, t4 = 13, …..
∵ t2 – t1 = t3 – t2 = t4 – t3 = 2, constant
∴ The reciprocal sequence is an A.P.
∴ The given sequence is H.P.

Question 2.
Find the nth term and hence find the 8th term of the following H.P.s:
(i) \(\frac{1}{2}, \frac{1}{5}, \frac{1}{8}, \frac{1}{11}, \ldots \ldots \ldots\)
(ii) \(\frac{1}{4}, \frac{1}{6}, \frac{1}{8}, \frac{1}{10}, \ldots \ldots \ldots \ldots\)
(iii) \(\frac{1}{5}, \frac{1}{10}, \frac{1}{15}, \frac{1}{20}, \cdots \cdots \cdots\)
Solution:


Question 3.
Find A.M. of two positive numbers whose G.M. and H.M. are 4 and \(\frac{16}{5}\).
Solution:
G.M. = 4, H.M. = \(\frac{16}{5}\)
∵ (G.M.)2 = (A.M.) (H.M.)
∴ 16 = A.M. × \(\frac{16}{5}\)
∴ A.M. = 5
Question 4.
Find H.M. of two positive numbers whose A.M. and G.M. are \(\frac{15}{2}\) and 6.
Solution:
A.M. = \(\frac{15}{2}\), G.M. = 6
Now, (G.M.)2 = (A.M.) (H.M.)
∴ 62 = \(\frac{15}{2}\) × H.M.
∴ H.M. = 36 × \(\frac{2}{15}\)
∴ H.M. = \(\frac{24}{5}\)
Question 5.
Find G.M. of two positive numbers whose A.M. and H.M. are 75 and 48.
Solution:
A.M. = 75, H.M. = 48
(G.M.)2 = (A.M.) (H.M.)
∵ (G.M.)2 = 75 × 48
∵ (G.M.)2 = 25 × 3 × 16 × 3
∵ (G.M.)2 = 52 × 42 × 32
∴ G.M. = 5 × 4 × 3
∴ G.M. = 60

Question 6.
Insert two numbers between \(\frac{1}{7}\) and \(\frac{1}{13}\) so that the resulting sequence is a H.P.
Solution:
Let the required numbers be \(\frac{1}{\mathrm{H}_{1}}\) and \(\frac{1}{\mathrm{H}_{2}}\).
∴ \(\frac{1}{7}, \frac{1}{\mathrm{H}_{1}}, \frac{1}{\mathrm{H}_{2}}, \frac{1}{13}\) are in H.P.
∴ 7, H1, H2 and 13 are in A.P.
∴ t1 = a = 7 and t4 = a + 3d = 13
∴ 7 + 3d = 13
∴ 3d = 6
∴ d = 2
∴ H1 = t2 = a + d = 7 + 2 = 9
and H2 = t3 = a + 2d = 7 + 2(2) = 11
∴ \(\frac{1}{9}\) and \(\frac{1}{11}\) are the required numbers to be inserted between \(\frac{1}{7}\) and \(\frac{1}{13}\) so that the resulting sequence is a H.P.
Question 7.
Insert two numbers between 1 and -27 so that the resulting sequence is a G.P.
Solution:
Let the required numbers be G1 and G2.
∴ 1, G1, G2, -27 are in G.P.
∴ t1 = 1, t2 = G1, t3 = G2, t4 = -27
∴ t1 = a = 1
tn = arn-1
∴ t4 = (1) r4-1
∴ -27 = r3
∴ r3 = (-3)3
∴ r = -3
∴ G1 = t2 = ar = 1(-3) = -3
∴ G2 = t3 = ar = 1(-3)2 = 9
∴ -3 and 9 are the required numbers to be inserted between 1 and -27 so that the resulting sequence is a G.P.
Question 8.
Find two numbers whose A.M. exceeds their G.M. by \(\frac{1}{2}\) and their H.M. by \(\frac{25}{26}\).
Solution:
Let a, b be the two numbers.
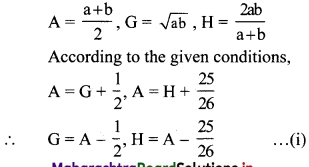

∴ a + b = 13
∴ b = 13 – a …….(iii)
and ab = 36
∴ a(13 – a) = 36 …… [From (iii)]
∴ a2 – 13a + 36 = 0
∴ (a – 4)(a – 9) = 0
∴ a = 4 or a = 9
When a = 4, b = 13 – 4 = 9
When a = 9, b = 13 – 9 = 4
∴ the two numbers are 4 and 9.

Question 9.
Find two numbers whose A.M. exceeds G.M. bv 7 and their H.M. by \(\frac{63}{5}\).
Solution:
Let a, b be the two numbers.

∴ a + b = 70
∴ b = 70 – a …..(ii)
∴ G = A – 7 = 35 – 7 = 28 …….[From (i)]
∴ √ab = 28
∴ ab = 282 = 784
∴ a(70 – a) = 784 ……[From (ii)]
∴ 70a – a2 = 784
∴ a2 – 70a + 784 = 0
∴ a2 – 56a – 14a + 784 = 0
∴ (a – 56) (a – 14) = 0
∴ a = 14 or a = 56
When a = 14, b = 70 – 14 = 56
When a = 56, b = 70 – 56 = 14
∴ the two numbers are 14 and 56.