Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf
Chapter 4 Sequences and Series Ex 4.5 Questions and Answers.
Question 1.
Find the sum \(\sum_{r=1}^{n}(r+1)(2 r-1)\).
Solution:

Question 2.
Find \(\sum_{r=1}^{n}\left(3 r^{2}-2 r+1\right)\).
Solution:


Question 3.
Find \(\sum_{r=1}^{n} \frac{1+2+3+\ldots+r}{r}\).
Solution:


Question 4.
Find \(\sum_{r=1}^{n} \frac{1^{3}+2^{3}+\ldots+r^{3}}{r(r+1)}\).
Solution:
We know that,

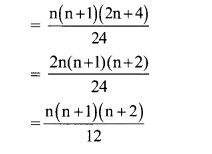
Question 5.
Find the sum 5 × 7 + 7 × 9 + 9 × 11 + 11 × 13 + …… upto n terms.
Solution:
5 × 7 + 7 × 9 + 9 × 11 + 11 × 13 + ….. upto n terms
Now, 5, 7, 9, 11, … are in A.P.
rth term = 5 + (r – 1) (2) = 2r + 3
7, 9, 11,. … are in A.P.
rth term = 7 + (r – 1) (2) = 2r + 5
∴ 5 × 7 + 7 × 9 + 9 × 11 + 11 × 13 + …… upto n terms

Question 6.
Find the sum 22 + 42 + 62 + 82 + …… upto n terms.
Solution:
22 + 42 + 62 + 82 + …… upto n terms
= (2 × 1)2 + (2 × 2)2 + (2 × 3)2 + (2 × 4)2 + ……

Question 7.
Find (702 – 692) + (682 – 672) + (662 – 652) + ……. + (22 – 12)
Solution:
Let S = (702 – 692) + (682 – 672) + …… +(22 – 12)
∴ S = (22 – 12) + (42 – 32) + …… + (702 – 692)
Here, 2, 4, 6,…, 70 is an A.P. with rth term = 2r
and 1, 3, 5,….., 69 in A.P. with rth term = 2r – 1


Question 8.
Find the sum 1 × 3 × 5 + 3 × 5 × 7 + 5 × 7 × 9 + …… + (2n – 1) (2n + 1) (2n + 3)
Solution:
1 × 3 × 5 + 3 × 5 × 7 + 5 × 7 × 9 + …… + (2n – 1) (2n + 1) (2n + 3)
Now, 1, 3, 5, 7, … are in A.P. with a = 1 and d = 2.
∴ rth term = 1 + (r – 1)2 = 2r – 1
3, 5, 7, 9, … are in A.P. with a = 3 and d = 2
∴ rth term = 3 + (r – 1)2 = 2r + 1
and 5, 7, 9, 11, … are in A.P. with a = 5 and d = 2
∴ rth term = 5 + (r – 1)2 = 2r + 3
∴ 1 × 3 × 5 + 3 × 5 × 7 + 5 × 7 × 9 + …… upto n terms

= n(n + 1)[2n(n + 1) + 4n + 2 – 1] – 3n
= n(n + l)(2n2 + 6n + 1) – 3n
= n(2n3 + 8n2 + 7n + 1 – 3)
= n(2n3 + 8n2 + 7n – 2)
Question 9.
Find n, if \(\frac{1 \times 2+2 \times 3+3 \times 4+4 \times 5+\ldots+\text { upto } n \text { terms }}{1+2+3+4+\ldots+\text { upto } n \text { terms }}\) = \(\frac{100}{3}\)
Solution:


Question 10.
If S1, S2, and S3 are the sums of first n natural numbers, their squares, and their cubes respectively, then show that:
9\(S_{2}^{2}\) = S3(1 + 8S1).
Solution:


Chapter 4 Sequences and Series Ex 4.5 Questions and Answers.
Question 1.
Find the sum \(\sum_{r=1}^{n}(r+1)(2 r-1)\).
Solution:

Question 2.
Find \(\sum_{r=1}^{n}\left(3 r^{2}-2 r+1\right)\).
Solution:


Question 3.
Find \(\sum_{r=1}^{n} \frac{1+2+3+\ldots+r}{r}\).
Solution:


Question 4.
Find \(\sum_{r=1}^{n} \frac{1^{3}+2^{3}+\ldots+r^{3}}{r(r+1)}\).
Solution:
We know that,

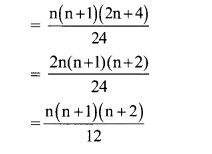
Question 5.
Find the sum 5 × 7 + 7 × 9 + 9 × 11 + 11 × 13 + …… upto n terms.
Solution:
5 × 7 + 7 × 9 + 9 × 11 + 11 × 13 + ….. upto n terms
Now, 5, 7, 9, 11, … are in A.P.
rth term = 5 + (r – 1) (2) = 2r + 3
7, 9, 11,. … are in A.P.
rth term = 7 + (r – 1) (2) = 2r + 5
∴ 5 × 7 + 7 × 9 + 9 × 11 + 11 × 13 + …… upto n terms

Question 6.
Find the sum 22 + 42 + 62 + 82 + …… upto n terms.
Solution:
22 + 42 + 62 + 82 + …… upto n terms
= (2 × 1)2 + (2 × 2)2 + (2 × 3)2 + (2 × 4)2 + ……

Question 7.
Find (702 – 692) + (682 – 672) + (662 – 652) + ……. + (22 – 12)
Solution:
Let S = (702 – 692) + (682 – 672) + …… +(22 – 12)
∴ S = (22 – 12) + (42 – 32) + …… + (702 – 692)
Here, 2, 4, 6,…, 70 is an A.P. with rth term = 2r
and 1, 3, 5,….., 69 in A.P. with rth term = 2r – 1


Question 8.
Find the sum 1 × 3 × 5 + 3 × 5 × 7 + 5 × 7 × 9 + …… + (2n – 1) (2n + 1) (2n + 3)
Solution:
1 × 3 × 5 + 3 × 5 × 7 + 5 × 7 × 9 + …… + (2n – 1) (2n + 1) (2n + 3)
Now, 1, 3, 5, 7, … are in A.P. with a = 1 and d = 2.
∴ rth term = 1 + (r – 1)2 = 2r – 1
3, 5, 7, 9, … are in A.P. with a = 3 and d = 2
∴ rth term = 3 + (r – 1)2 = 2r + 1
and 5, 7, 9, 11, … are in A.P. with a = 5 and d = 2
∴ rth term = 5 + (r – 1)2 = 2r + 3
∴ 1 × 3 × 5 + 3 × 5 × 7 + 5 × 7 × 9 + …… upto n terms

= n(n + 1)[2n(n + 1) + 4n + 2 – 1] – 3n
= n(n + l)(2n2 + 6n + 1) – 3n
= n(2n3 + 8n2 + 7n + 1 – 3)
= n(2n3 + 8n2 + 7n – 2)
Question 9.
Find n, if \(\frac{1 \times 2+2 \times 3+3 \times 4+4 \times 5+\ldots+\text { upto } n \text { terms }}{1+2+3+4+\ldots+\text { upto } n \text { terms }}\) = \(\frac{100}{3}\)
Solution:


Question 10.
If S1, S2, and S3 are the sums of first n natural numbers, their squares, and their cubes respectively, then show that:
9\(S_{2}^{2}\) = S3(1 + 8S1).
Solution:

