Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf
Chapter 4 Sequences and Series Miscellaneous Exercise 4 Questions and Answers.
Question 1.
In a G.P., the fourth term is 48 and the eighth term is 768. Find the tenth term.
Solution:

Question 2.
For a G.P. a = \(\frac{4}{3}\) and t7 = \(\frac{243}{1024}\), find the value of r.
Solution:
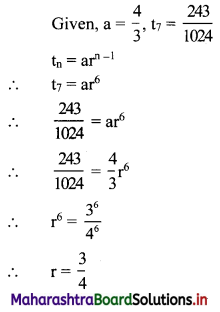

Question 3.
For a sequence, if tn = \(\frac{5^{n-2}}{7^{n-3}}\), verify whether the sequence is a G.P. If it is a G.P., find its first term and the common ratio.
Solution:
The sequence (tn) is a G.P., if \(\frac{5^{n-2}}{7^{n-3}}\) = constant, for all n ∈ N.

∴ the sequence is a G.P. with common ratio = \(\frac{5}{7}\)
∴ first term = t1 = \(\frac{5^{1-2}}{7^{1-3}}=\frac{5^{-1}}{7^{-2}}=\frac{7^{2}}{5}=\frac{49}{5}\)
Question 4.
Find three numbers in G.P., such that their sum is 35 and their product is 1000.
Solution:
Let the three numbers in G.P. be \(\frac{a}{r}\), a, ar.
According to the first condition,


∴ the three numbers in G.P. are 20, 10, 5 or 5, 10, 20.
Question 5.
Find 4 numbers in G. P. such that the sum of the middle 2 numbers is \(\frac{10}{3}\) and their product is 1.
Solution:
Let the four numbers in G.P. be \(\frac{a}{r^{3}}, \frac{a}{r}, a r, a r^{3}\).
According to the second condition,
\(\frac{\mathrm{a}}{\mathrm{r}^{3}}\left(\frac{\mathrm{a}}{\mathrm{r}}\right)(\mathrm{ar})\left(\mathrm{ar}^{3}\right)=1\)
∴ a4 = 1
∴ a = 1
According to the first condition,


Question 6.
Find five numbers in G.P. such that their product is 243 and the sum of the second and fourth numbers is 10.
Solution:
Let the five numbers in G.P. be
\(\frac{a}{r^{2}}, \frac{a}{r}, a, a r, a r^{2}\)
According to the first condition,


Question 7.
For a sequence, Sn = 4(7n – 1), verify whether the sequence is a G.P.
Solution:

Question 8.
Find 2 + 22 + 222 + 2222 + …… upto n terms.
Solution:
Sn = 2 + 22 + 222 +….. upto n terms
= 2(1 + 11 + 111 +…… upto n terms)
= \(\frac{2}{9}\) (9 + 99 + 999 + … upto n terms)
= \(\frac{2}{9}\) [(10 – 1) + (100 – 1) + (1000 – 1) +…… upto n terms]
= \(\frac{2}{9}\) [(10 + 100 + 1000 + … upto n terms) – (1 + 1 + 1 + ….. n times)]
Since, 10, 100, 1000, …… n terms are in G.P.
with a = 10, r = \(\frac{100}{10}\) = 10
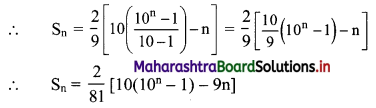
Question 9.
Find the nth term of the sequence 0.6, 0.66, 0.666, 0.6666,…..
Solution:
0.6, 0.66, 0.666, 0.6666, ……
∴ t1 = 0.6
t2 = 0.66 = 0.6 + 0.06
t3 = 0.666 = 0.6 + 0.06 + 0.006
Hence, in general
tn = 0.6 + 0.06 + 0.006 + …… upto n terms.
The terms are in G.P.with
a = 0.6, r = \(\frac{0.06}{0.6}\) = 0.1
∴ tn = the sum of first n terms of the G.P.
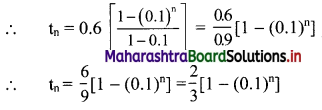

Question 10.
Find \(\sum_{r=1}^{n}\left(5 r^{2}+4 r-3\right)\).
Solution:

Question 11.
Find \(\sum_{\mathbf{r}=1}^{\mathbf{n}} \mathbf{r}(\mathbf{r}-\mathbf{3})(\mathbf{r}-\mathbf{2})\).
Solution:

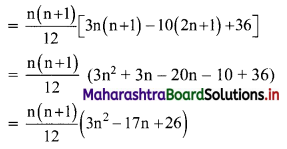
Question 12.
Find \(\sum_{r=1}^{n} \frac{1^{2}+2^{2}+3^{2}+\ldots+r^{2}}{2 r+1}\)
Solution:
We know that,

Question 13.
Find \(\sum_{r=1}^{n} \frac{1^{3}+2^{3}+3^{3}+\ldots+r^{3}}{(r+1)^{2}}\)
Solution:
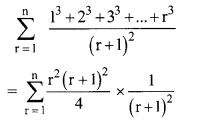
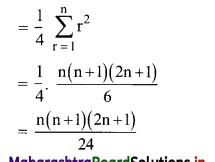
Question 14.
Find 2 × 6 + 4 × 9 + 6 × 12 + …… upto n terms.
Solution:
2, 4, 6, … are in A.P.
∴ rth term = 2 + (r – 1)2 = 2r
6, 9, 12, … are in A.P.
∴ rth term = 6 + (r – 1) (3) = (3r + 3)
∴ 2 × 6 + 4 × 9 + 6 × 12 +…… upto n terms
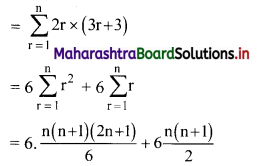
= n(n + 1) (2n + 1 + 3)
= 2n(n + 1)(n + 2)

Question 15.
Find 122 + 132 + 142 + 152 + …… + 202.
Solution:
122 + 132 + 142 + 152 + …… + 202
= (12 + 22 + 32 + 42 + ……. + 202) – (12 + 22 + 32 + 42 + …… + 112)
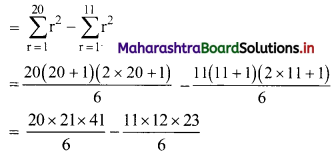
= 2870 – 506
= 2364
Question 16.
Find (502 – 492) + (482 – 472) + (462 – 452) + …… + (22 – 12).
Solution:
(502 – 492) + (482 – 472) + (462 – 452) + …… + (22 – 12)
= (502 + 482 + 462 + …… + 22) – (492 + 472 + 452 + …… + 12)
= \(\sum_{r=1}^{25}(2 r)^{2}-\sum_{r=1}^{25}(2 r-1)^{2}\)

= 1300 – 25
= 1275
Question 17.
In a G.P., if t2 = 7, t4 = 1575, find r.
Solution:

Question 18.
Find k so that k – 1, k, k + 2 are consecutive terms of a G.P.
Solution:
Since k – 1, k, k + 2 are consecutive terms of a G.P.
∴ \(\frac{k}{k-1}=\frac{k+2}{k}\)
∴ k2 = k2 + k – 2
∴ k – 2 = 0
∴ k = 2

Question 19.
If pth, qth and rth terms of a G.P. are x, y, z respectively, find the value of \(x^{q-r} \cdot y^{r-p} \cdot z^{p-q}\).
Solution:
Let a be the first term and R be the common ratio of the G.P.
∴ tn = \(\text { a. } R^{n-1}\)
∴ x = \(\text { a. } R^{p-1}\), y = \(\text { a. } R^{q-1}\), z = \(\text { a. } R^{r-1}\)

Chapter 4 Sequences and Series Miscellaneous Exercise 4 Questions and Answers.
Question 1.
In a G.P., the fourth term is 48 and the eighth term is 768. Find the tenth term.
Solution:

Question 2.
For a G.P. a = \(\frac{4}{3}\) and t7 = \(\frac{243}{1024}\), find the value of r.
Solution:
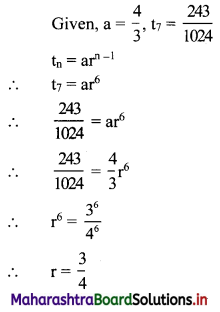

Question 3.
For a sequence, if tn = \(\frac{5^{n-2}}{7^{n-3}}\), verify whether the sequence is a G.P. If it is a G.P., find its first term and the common ratio.
Solution:
The sequence (tn) is a G.P., if \(\frac{5^{n-2}}{7^{n-3}}\) = constant, for all n ∈ N.

∴ the sequence is a G.P. with common ratio = \(\frac{5}{7}\)
∴ first term = t1 = \(\frac{5^{1-2}}{7^{1-3}}=\frac{5^{-1}}{7^{-2}}=\frac{7^{2}}{5}=\frac{49}{5}\)
Question 4.
Find three numbers in G.P., such that their sum is 35 and their product is 1000.
Solution:
Let the three numbers in G.P. be \(\frac{a}{r}\), a, ar.
According to the first condition,


∴ the three numbers in G.P. are 20, 10, 5 or 5, 10, 20.
Question 5.
Find 4 numbers in G. P. such that the sum of the middle 2 numbers is \(\frac{10}{3}\) and their product is 1.
Solution:
Let the four numbers in G.P. be \(\frac{a}{r^{3}}, \frac{a}{r}, a r, a r^{3}\).
According to the second condition,
\(\frac{\mathrm{a}}{\mathrm{r}^{3}}\left(\frac{\mathrm{a}}{\mathrm{r}}\right)(\mathrm{ar})\left(\mathrm{ar}^{3}\right)=1\)
∴ a4 = 1
∴ a = 1
According to the first condition,


Question 6.
Find five numbers in G.P. such that their product is 243 and the sum of the second and fourth numbers is 10.
Solution:
Let the five numbers in G.P. be
\(\frac{a}{r^{2}}, \frac{a}{r}, a, a r, a r^{2}\)
According to the first condition,


Question 7.
For a sequence, Sn = 4(7n – 1), verify whether the sequence is a G.P.
Solution:

Question 8.
Find 2 + 22 + 222 + 2222 + …… upto n terms.
Solution:
Sn = 2 + 22 + 222 +….. upto n terms
= 2(1 + 11 + 111 +…… upto n terms)
= \(\frac{2}{9}\) (9 + 99 + 999 + … upto n terms)
= \(\frac{2}{9}\) [(10 – 1) + (100 – 1) + (1000 – 1) +…… upto n terms]
= \(\frac{2}{9}\) [(10 + 100 + 1000 + … upto n terms) – (1 + 1 + 1 + ….. n times)]
Since, 10, 100, 1000, …… n terms are in G.P.
with a = 10, r = \(\frac{100}{10}\) = 10
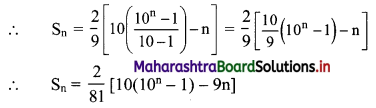
Question 9.
Find the nth term of the sequence 0.6, 0.66, 0.666, 0.6666,…..
Solution:
0.6, 0.66, 0.666, 0.6666, ……
∴ t1 = 0.6
t2 = 0.66 = 0.6 + 0.06
t3 = 0.666 = 0.6 + 0.06 + 0.006
Hence, in general
tn = 0.6 + 0.06 + 0.006 + …… upto n terms.
The terms are in G.P.with
a = 0.6, r = \(\frac{0.06}{0.6}\) = 0.1
∴ tn = the sum of first n terms of the G.P.
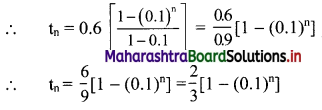

Question 10.
Find \(\sum_{r=1}^{n}\left(5 r^{2}+4 r-3\right)\).
Solution:

Question 11.
Find \(\sum_{\mathbf{r}=1}^{\mathbf{n}} \mathbf{r}(\mathbf{r}-\mathbf{3})(\mathbf{r}-\mathbf{2})\).
Solution:

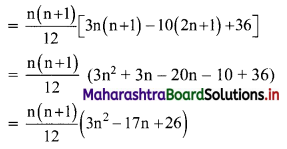
Question 12.
Find \(\sum_{r=1}^{n} \frac{1^{2}+2^{2}+3^{2}+\ldots+r^{2}}{2 r+1}\)
Solution:
We know that,

Question 13.
Find \(\sum_{r=1}^{n} \frac{1^{3}+2^{3}+3^{3}+\ldots+r^{3}}{(r+1)^{2}}\)
Solution:
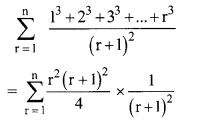
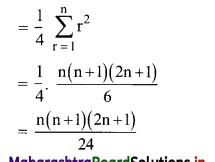
Question 14.
Find 2 × 6 + 4 × 9 + 6 × 12 + …… upto n terms.
Solution:
2, 4, 6, … are in A.P.
∴ rth term = 2 + (r – 1)2 = 2r
6, 9, 12, … are in A.P.
∴ rth term = 6 + (r – 1) (3) = (3r + 3)
∴ 2 × 6 + 4 × 9 + 6 × 12 +…… upto n terms
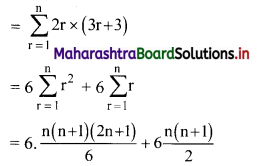
= n(n + 1) (2n + 1 + 3)
= 2n(n + 1)(n + 2)

Question 15.
Find 122 + 132 + 142 + 152 + …… + 202.
Solution:
122 + 132 + 142 + 152 + …… + 202
= (12 + 22 + 32 + 42 + ……. + 202) – (12 + 22 + 32 + 42 + …… + 112)
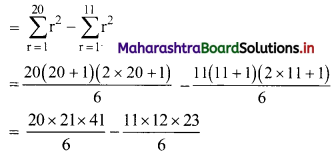
= 2870 – 506
= 2364
Question 16.
Find (502 – 492) + (482 – 472) + (462 – 452) + …… + (22 – 12).
Solution:
(502 – 492) + (482 – 472) + (462 – 452) + …… + (22 – 12)
= (502 + 482 + 462 + …… + 22) – (492 + 472 + 452 + …… + 12)
= \(\sum_{r=1}^{25}(2 r)^{2}-\sum_{r=1}^{25}(2 r-1)^{2}\)

= 1300 – 25
= 1275
Question 17.
In a G.P., if t2 = 7, t4 = 1575, find r.
Solution:

Question 18.
Find k so that k – 1, k, k + 2 are consecutive terms of a G.P.
Solution:
Since k – 1, k, k + 2 are consecutive terms of a G.P.
∴ \(\frac{k}{k-1}=\frac{k+2}{k}\)
∴ k2 = k2 + k – 2
∴ k – 2 = 0
∴ k = 2

Question 19.
If pth, qth and rth terms of a G.P. are x, y, z respectively, find the value of \(x^{q-r} \cdot y^{r-p} \cdot z^{p-q}\).
Solution:
Let a be the first term and R be the common ratio of the G.P.
∴ tn = \(\text { a. } R^{n-1}\)
∴ x = \(\text { a. } R^{p-1}\), y = \(\text { a. } R^{q-1}\), z = \(\text { a. } R^{r-1}\)
