Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf
Chapter 6 Determinants Miscellaneous Exercise 6 Questions and Answers.
Question 1.
Evaluate:
(i) \(\left|\begin{array}{ccc}
2 & -5 & 7 \\
5 & 2 & 1 \\
9 & 0 & 2
\end{array}\right|\)
Solution:
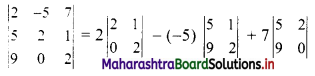
= 2(4 – 0) + 5(10 – 9) + 7(0 – 18)
= 2(4) + 5(1) + 7(-18)
= 8 + 5 – 126
= -113
(ii) \(\left|\begin{array}{ccc}
1 & -3 & 12 \\
0 & 2 & -4 \\
9 & 7 & 2
\end{array}\right|\)
Solution:
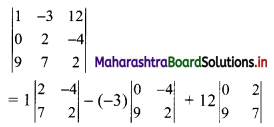
= 1(4 + 28) + 3(0 + 36) + 12(0 – 18)
= 1(32) + 3(36) + 12(-18)
= 32 + 108 – 216
= -76

Question 2.
Find the value(s) of x, if
(i) \(\left|\begin{array}{ccc}
1 & 4 & 20 \\
1 & -2 & -5 \\
1 & 2 x & 5 x^{2}
\end{array}\right|=0\)
Solution:
\(\left|\begin{array}{ccc}
1 & 4 & 20 \\
1 & -2 & -5 \\
1 & 2 x & 5 x^{2}
\end{array}\right|=0\)
∴ 1(-10x2 + 10x) – 4(5x2 + 5) + 20(2x + 2) = 0
∴ -10x2 + 10x – 20x2 – 20 + 40x + 40 = 0
∴ -30x2 + 50x + 20 = 0
∴ 3x2 – 5x – 2 = 0 ……[Dividing throughout by (-10)]
∴ 3x2 – 6x + x – 2 = 0
∴ 3x(x – 2) + 1(x – 2) = 0
∴ (x – 2) (3x + 1) = 0
∴ x – 2 = 0 or 3x + 1 = 0
∴ x = 2 or x = \(-\frac{1}{3}\)
(ii) \(\left|\begin{array}{ccc}
1 & 2 x & 4 x \\
1 & 4 & 16 \\
1 & 1 & 1
\end{array}\right|=0\)
Solution:
\(\left|\begin{array}{ccc}
1 & 2 x & 4 x \\
1 & 4 & 16 \\
1 & 1 & 1
\end{array}\right|=0\)
∴ 1(4 – 16) – 2x(1 – 16) + 4x(1 – 4) = 0
∴ 1(-12) – 2x(-15) + 4x(-3) = 0
∴ -12 + 30x – 12x = 0
∴ 18x = 12
∴ x = \(\frac{2}{3}\)
Question 3.
By using properties of determinants, prove that \(\left|\begin{array}{ccc}
x+y & y+z & z+x \\
z & x & y \\
1 & 1 & 1
\end{array}\right|=0\).
Solution:


Question 4.
Without expanding the determinants, show that

Solution:

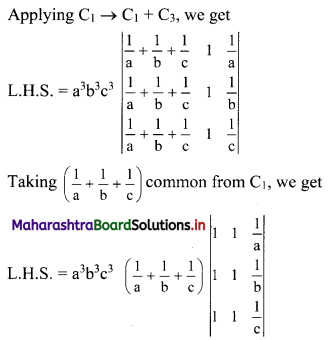



Question 5.
Solve the following linear equations by Cramer’s Rule.
(i) 2x – y + z = 1, x + 2y + 3z = 8, 3x + y – 4z = 1
Solution:
Given equations are
2x – y + z = 1
x + 2y + 3z = 8
3x + y – 4z = 1
D = \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 2 & 3 \\
3 & 1 & -4
\end{array}\right|\)
= 2(-8 – 3) – (-1)(-4 – 9) + 1(1 – 6)
= 2(-11) + 1(-13) + 1(-5)
= -22 – 13 – 5
= -40 ≠ 0
Dx = \(\left|\begin{array}{ccc}
1 & -1 & 1 \\
8 & 2 & 3 \\
1 & 1 & -4
\end{array}\right|\)
= 1(-8 – 3) – (-1)(-32 – 3) + 1(8 – 2)
= 1(-11) + 1(-35) + 1(6)
= -11 – 35 + 6
= -40
Dy = \(\left|\begin{array}{ccc}
2 & 1 & 1 \\
1 & 8 & 3 \\
3 & 1 & -4
\end{array}\right|\)
= 2(-32 – 3) – 1(-4 – 9) + 1(1 – 24)
= 2(-35) – 1(-13) + 1(-23)
= -70 + 13 – 23
= -80
Dz = \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 2 & 8 \\
3 & 1 & 1
\end{array}\right|\)
= 2(2 – 8) – (-1)(1 – 24) + 1(1 – 6)
= 2(-6) + 1(-23) + 1(-5)
= -12 – 23 – 5
= -40
By Cramer’s Rule,
x = \(\frac{D_{x}}{D}=\frac{-40}{-40}\) = 1
y = \(\frac{\mathrm{D}_{y}}{\mathrm{D}}=\frac{-80}{-40}\) = 2
z = \(\frac{\mathrm{D}_{z}}{\mathrm{D}}=\frac{-40}{-40}\) = 1
∴ x = 1, y = 2 and z = 1 are the solutions of the given equations.

(ii) \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=-2\), \(\frac{1}{x}-\frac{2}{y}+\frac{1}{z}=3\), \(\frac{2}{x}-\frac{1}{y}+\frac{3}{z}=-1\)
Solution:
Let \(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q, \(\frac{1}{z}\) = r
The given equations become
p + q + r = -2
p – 2q + r = 3
2p – q + 3r = -1
D = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & -2 & 1 \\
2 & -1 & 3
\end{array}\right|\)
= 1(-6 + 1) – 1(3 – 2) + 1(-1 + 4)
= -5 – 1 + 3
= -3
Dp = \(\left|\begin{array}{rrr}
-2 & 1 & 1 \\
3 & -2 & 1 \\
-1 & -1 & 3
\end{array}\right|\)
= -2(-6 + 1) – 1(9 + 1) + 1(-3 – 2)
= 10 – 10 – 5
= -5
Dq = \(\left|\begin{array}{ccc}
1 & -2 & 1 \\
1 & 3 & 1 \\
2 & -1 & 3
\end{array}\right|\)
= 1(9 + 1) + 2(3 – 2) + 1(-1 – 6)
= 10 + 2 – 7
= 5
Dr = \(\left|\begin{array}{rrr}
1 & 1 & -2 \\
1 & -2 & 3 \\
2 & -1 & -1
\end{array}\right|\)
= 1(2 + 3) – 1(-1 – 6) – 2(-1 + 4)
= 5 + 7 – 6
= 6
By Cramer’s Rule,
p = \(\frac{\mathrm{D}_{\mathrm{p}}}{\mathrm{D}}=\frac{-5}{-3}=\frac{5}{3}\)
q = \(\frac{\mathrm{D}_{y}}{\mathrm{D}}=\frac{-80}{-40}\) = 2
r = \(\frac{D_{2}}{D}=\frac{-40}{-40}\) = 1
∴ x = \(\frac{3}{5}\), y = \(\frac{-3}{5}\), z = \(\frac{-1}{2}\) are the solutions of the given equations.
(iii) x – y + 2z = 7, 3x + 4y – 5z = 5, 2x – y + 3z = 12
Solution:
Given equations are
x – y + 2z = 1
3x + 4y – 5z = 5
2x – y + 3z = 12
D = \(\left|\begin{array}{ccc}
1 & -1 & 2 \\
3 & 4 & -5 \\
2 & -1 & 3
\end{array}\right|\)
= 1(12 – 5) – (-1)(9 + 10) + 2(-3 – 8)
= 1(7) + 1(19) + 2(-11)
= 7 + 19 – 22
= 4 ≠ 0
Dx = \(\left|\begin{array}{ccc}
7 & -1 & 2 \\
5 & 4 & -5 \\
12 & -1 & 3
\end{array}\right|\)
= 7(12 – 5) – (-1)(15 + 60) + 2(-5 – 48)
= 7(7)+ 1(75) +2(-53)
= 49 + 75 – 106
= 18
Dy = \(\left|\begin{array}{ccc}
1 & 7 & 2 \\
3 & 5 & -5 \\
2 & 12 & 3
\end{array}\right|\)
= 1(15 + 60) – 7(9 + 10) + 2(36 – 10)
= 1(75) – 7(19) + 2(26)
= 75 – 133 + 52
= -6
Dz = \(\left|\begin{array}{ccc}
1 & -1 & 7 \\
3 & 4 & 5 \\
2 & -1 & 12
\end{array}\right|\)
= 1(48 + 5) – (-1)(36 – 10) + 7(-3 – 8)
= 1(53)+ 1(26) + 7(-11)
= 53 + 26 – 77
= 2
By Cramer’s Rule,
x = \(\frac{\mathrm{D}_{x}}{\mathrm{D}}=\frac{18}{4}=\frac{9}{2}\)
y = \(\frac{D_{y}}{D}=\frac{-6}{4}=\frac{-3}{2}\)
z = \(\frac{D_{z}}{D}=\frac{2}{4}=\frac{1}{2}\)
∴ x = \(\frac{9}{2}\), y = \(\frac{-3}{2}\) and z = \(\frac{1}{2}\) are the solutions of the given equations.

Question 6.
Find the value(s) of k, if the following equations are consistent.
(i) 3x + y – 2 = 0, kx + 2y – 3 = 0 and 2x – y = 3
Solution:
Given equations are
3x + y – 2 = 0
kx + 2y – 3 = 0
2x – y = 3 i.e. 2x – y – 3 = 0
Since, these equations are consistent.
∴ \(\left|\begin{array}{rrr}
3 & 1 & -2 \\
k & 2 & -3 \\
2 & -1 & -3
\end{array}\right|=0\)
∴ 3(-6 – 3) – 1(-3k + 6) – 2(-k – 4) = 0
∴ 3(-9) – 1 (-3k + 6) – 2(-k – 4) = 0
∴ -27 + 3k – 6 + 2k + 8 = 0
∴ 5k – 25 = 0
∴ k = 5
(ii) kx + 3y + 4 = 0, x + ky + 3 = 0, 3x + 4y + 5 = 0
Solution:
Given equations are
kx + 3y + 4 = 0
x + ky + 3 = 0
3x + 4y + 5 = 0
Since, these equations are consistent.
∴ \(\left|\begin{array}{lll}
\mathrm{k} & 3 & 4 \\
1 & \mathrm{k} & 3 \\
3 & 4 & 5
\end{array}\right|=0\)
∴ k(5k – 12) – 3(5 – 9) + 4(4 – 3k) = 0
∴ 5k2 – 12k + 12 + 16 – 12k = 0
∴ 5k2 – 24k + 28 = 0
∴ 5k2 – 10k – 14k + 28 = 0
∴ 5k(k – 2) – 14(k – 2) = 0
∴ (k – 2) (5k – 14) = 0
∴ k – 2 = 0 or 5k – 14 = 0
∴ k = 2 or k = \(\frac{14}{5}\)
Question 7.
Find the area of triangles whose vertices are
(i) A(-1, 2), B(2, 4), C(0, 0)
Solution:
Here, A(x1, y1) ≡ A(-1, 2), B(x2, y2) ≡ B(2, 4), C(x3, y3) ≡ C(0, 0)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ A(∆ABC) = \(\frac{1}{2}\left|\begin{array}{ccc}
-1 & 2 & 1 \\
2 & 4 & 1 \\
0 & 0 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [-1(4 – 0) – 2(2 – 0) + 1(0 – 0)]
= \(\frac{1}{2}\) (-4 – 4)
= \(\frac{1}{2}\) (-8)
= -4
Since, area cannot be negative.
∴ A(∆ABC) = 4 sq.units
(ii) P(3, 6), Q(-1, 3), R(2, -1)
Solution:
Here, P(x1, y1) ≡ P(3, 6), Q(x2, y2) ≡ Q(-1, 3), R(x3, y3) ≡ R(2, -1)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
A(∆PQR) = \(\frac{1}{2}\left|\begin{array}{ccc}
3 & 6 & 1 \\
-1 & 3 & 1 \\
2 & -1 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [3(3 + 1) – 6(-1 – 2) + 1(1 – 6)]
= \(\frac{1}{2}\) [3(4) – 6(-3) + 1(-5)]
= \(\frac{1}{2}\) (12 + 18 – 5)
∴ A(∆PQR) = \(\frac{25}{2}\) sq.units

(iii) L(1, 1), M(-2, 2), N(5, 4)
Solution:
Here, L(x1, y1) ≡ L(1, 1), M(x2, y2) ≡ M(-2, 2), N(x3, y3) ≡ N(5, 4)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
A(∆LMN) = \(\frac{1}{2}\left|\begin{array}{rrr}
1 & 1 & 1 \\
-2 & 2 & 1 \\
5 & 4 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [1(2 – 4) -1(-2 – 5) + 1(-8 – 10)]
= \(\frac{1}{2}\) [1(-2) – 1(-7) + 1(-18)]
= \(\frac{1}{2}\) (-2 + 7 – 18)
= \(\frac{-13}{2}\)
Since, area cannot be negative.
∴ A(∆LMN) = \(\frac{13}{2}\) sq.units
Question 8.
Find the value of k,
(i) if the area of ∆PQR is 4 square units and vertices are P(k, 0), Q(4, 0), R(0, 2).
Solution:
Here, P(x1, y1) ≡ P(k, 0), Q(x2, y2) ≡ Q(4, 0), R(x3, y3) ≡ R(0, 2)
A(∆PQR) = 4 sq.units
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ ±4 = \(\frac{1}{2}\left|\begin{array}{lll}
k & 0 & 1 \\
4 & 0 & 1 \\
0 & 2 & 1
\end{array}\right|\)
∴ ±4 = \(\frac{1}{2}\) [k(0 – 2) – 0 + 1(8 – 0)]
∴ ±8 = -2k + 8
∴ 8 = -2k + 8 or -8 = -2k + 8
∴ -2k = 0 or 2k = 16
∴ k = 0 or k = 8

(ii) if area of ∆LMN is \(\frac{33}{2}\) square units and vertices are L(3, -5), M(-2, k), N(1, 4).
Solution:
Here, L(x1, y1) ≡ L(3, -5), M(x2, y2) ≡ M(-2, k), N(x3, y3) ≡ N(1, 4)
A(∆LMN) = \(\frac{33}{2}\) sq.units
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ \(\pm \frac{33}{2}=\frac{1}{2}\left|\begin{array}{ccc}
3 & -5 & 1 \\
-2 & \mathrm{k} & 1 \\
1 & 4 & 1
\end{array}\right|\)
∴ ±\(\frac{33}{2}\) = \(\frac{1}{2}\) [3(k – 4) – (-5) (-2 – 1) + 1(-8 – k)]
∴ ±33 = 3k – 12 – 15 – 8 – k
∴ 33 = 2k – 35
∴ 2k – 35 = 33 or 2k – 35 = -33
∴ 2k = 68 or 2k = 2
∴ k = 34 or k = 1
Chapter 6 Determinants Miscellaneous Exercise 6 Questions and Answers.
Question 1.
Evaluate:
(i) \(\left|\begin{array}{ccc}
2 & -5 & 7 \\
5 & 2 & 1 \\
9 & 0 & 2
\end{array}\right|\)
Solution:
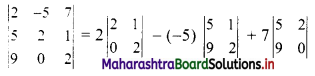
= 2(4 – 0) + 5(10 – 9) + 7(0 – 18)
= 2(4) + 5(1) + 7(-18)
= 8 + 5 – 126
= -113
(ii) \(\left|\begin{array}{ccc}
1 & -3 & 12 \\
0 & 2 & -4 \\
9 & 7 & 2
\end{array}\right|\)
Solution:
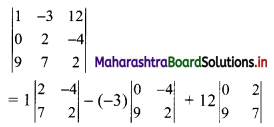
= 1(4 + 28) + 3(0 + 36) + 12(0 – 18)
= 1(32) + 3(36) + 12(-18)
= 32 + 108 – 216
= -76

Question 2.
Find the value(s) of x, if
(i) \(\left|\begin{array}{ccc}
1 & 4 & 20 \\
1 & -2 & -5 \\
1 & 2 x & 5 x^{2}
\end{array}\right|=0\)
Solution:
\(\left|\begin{array}{ccc}
1 & 4 & 20 \\
1 & -2 & -5 \\
1 & 2 x & 5 x^{2}
\end{array}\right|=0\)
∴ 1(-10x2 + 10x) – 4(5x2 + 5) + 20(2x + 2) = 0
∴ -10x2 + 10x – 20x2 – 20 + 40x + 40 = 0
∴ -30x2 + 50x + 20 = 0
∴ 3x2 – 5x – 2 = 0 ……[Dividing throughout by (-10)]
∴ 3x2 – 6x + x – 2 = 0
∴ 3x(x – 2) + 1(x – 2) = 0
∴ (x – 2) (3x + 1) = 0
∴ x – 2 = 0 or 3x + 1 = 0
∴ x = 2 or x = \(-\frac{1}{3}\)
(ii) \(\left|\begin{array}{ccc}
1 & 2 x & 4 x \\
1 & 4 & 16 \\
1 & 1 & 1
\end{array}\right|=0\)
Solution:
\(\left|\begin{array}{ccc}
1 & 2 x & 4 x \\
1 & 4 & 16 \\
1 & 1 & 1
\end{array}\right|=0\)
∴ 1(4 – 16) – 2x(1 – 16) + 4x(1 – 4) = 0
∴ 1(-12) – 2x(-15) + 4x(-3) = 0
∴ -12 + 30x – 12x = 0
∴ 18x = 12
∴ x = \(\frac{2}{3}\)
Question 3.
By using properties of determinants, prove that \(\left|\begin{array}{ccc}
x+y & y+z & z+x \\
z & x & y \\
1 & 1 & 1
\end{array}\right|=0\).
Solution:


Question 4.
Without expanding the determinants, show that

Solution:





Question 5.
Solve the following linear equations by Cramer’s Rule.
(i) 2x – y + z = 1, x + 2y + 3z = 8, 3x + y – 4z = 1
Solution:
Given equations are
2x – y + z = 1
x + 2y + 3z = 8
3x + y – 4z = 1
D = \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 2 & 3 \\
3 & 1 & -4
\end{array}\right|\)
= 2(-8 – 3) – (-1)(-4 – 9) + 1(1 – 6)
= 2(-11) + 1(-13) + 1(-5)
= -22 – 13 – 5
= -40 ≠ 0
Dx = \(\left|\begin{array}{ccc}
1 & -1 & 1 \\
8 & 2 & 3 \\
1 & 1 & -4
\end{array}\right|\)
= 1(-8 – 3) – (-1)(-32 – 3) + 1(8 – 2)
= 1(-11) + 1(-35) + 1(6)
= -11 – 35 + 6
= -40
Dy = \(\left|\begin{array}{ccc}
2 & 1 & 1 \\
1 & 8 & 3 \\
3 & 1 & -4
\end{array}\right|\)
= 2(-32 – 3) – 1(-4 – 9) + 1(1 – 24)
= 2(-35) – 1(-13) + 1(-23)
= -70 + 13 – 23
= -80
Dz = \(\left|\begin{array}{ccc}
2 & -1 & 1 \\
1 & 2 & 8 \\
3 & 1 & 1
\end{array}\right|\)
= 2(2 – 8) – (-1)(1 – 24) + 1(1 – 6)
= 2(-6) + 1(-23) + 1(-5)
= -12 – 23 – 5
= -40
By Cramer’s Rule,
x = \(\frac{D_{x}}{D}=\frac{-40}{-40}\) = 1
y = \(\frac{\mathrm{D}_{y}}{\mathrm{D}}=\frac{-80}{-40}\) = 2
z = \(\frac{\mathrm{D}_{z}}{\mathrm{D}}=\frac{-40}{-40}\) = 1
∴ x = 1, y = 2 and z = 1 are the solutions of the given equations.

(ii) \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=-2\), \(\frac{1}{x}-\frac{2}{y}+\frac{1}{z}=3\), \(\frac{2}{x}-\frac{1}{y}+\frac{3}{z}=-1\)
Solution:
Let \(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q, \(\frac{1}{z}\) = r
The given equations become
p + q + r = -2
p – 2q + r = 3
2p – q + 3r = -1
D = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & -2 & 1 \\
2 & -1 & 3
\end{array}\right|\)
= 1(-6 + 1) – 1(3 – 2) + 1(-1 + 4)
= -5 – 1 + 3
= -3
Dp = \(\left|\begin{array}{rrr}
-2 & 1 & 1 \\
3 & -2 & 1 \\
-1 & -1 & 3
\end{array}\right|\)
= -2(-6 + 1) – 1(9 + 1) + 1(-3 – 2)
= 10 – 10 – 5
= -5
Dq = \(\left|\begin{array}{ccc}
1 & -2 & 1 \\
1 & 3 & 1 \\
2 & -1 & 3
\end{array}\right|\)
= 1(9 + 1) + 2(3 – 2) + 1(-1 – 6)
= 10 + 2 – 7
= 5
Dr = \(\left|\begin{array}{rrr}
1 & 1 & -2 \\
1 & -2 & 3 \\
2 & -1 & -1
\end{array}\right|\)
= 1(2 + 3) – 1(-1 – 6) – 2(-1 + 4)
= 5 + 7 – 6
= 6
By Cramer’s Rule,
p = \(\frac{\mathrm{D}_{\mathrm{p}}}{\mathrm{D}}=\frac{-5}{-3}=\frac{5}{3}\)
q = \(\frac{\mathrm{D}_{y}}{\mathrm{D}}=\frac{-80}{-40}\) = 2
r = \(\frac{D_{2}}{D}=\frac{-40}{-40}\) = 1
∴ x = \(\frac{3}{5}\), y = \(\frac{-3}{5}\), z = \(\frac{-1}{2}\) are the solutions of the given equations.
(iii) x – y + 2z = 7, 3x + 4y – 5z = 5, 2x – y + 3z = 12
Solution:
Given equations are
x – y + 2z = 1
3x + 4y – 5z = 5
2x – y + 3z = 12
D = \(\left|\begin{array}{ccc}
1 & -1 & 2 \\
3 & 4 & -5 \\
2 & -1 & 3
\end{array}\right|\)
= 1(12 – 5) – (-1)(9 + 10) + 2(-3 – 8)
= 1(7) + 1(19) + 2(-11)
= 7 + 19 – 22
= 4 ≠ 0
Dx = \(\left|\begin{array}{ccc}
7 & -1 & 2 \\
5 & 4 & -5 \\
12 & -1 & 3
\end{array}\right|\)
= 7(12 – 5) – (-1)(15 + 60) + 2(-5 – 48)
= 7(7)+ 1(75) +2(-53)
= 49 + 75 – 106
= 18
Dy = \(\left|\begin{array}{ccc}
1 & 7 & 2 \\
3 & 5 & -5 \\
2 & 12 & 3
\end{array}\right|\)
= 1(15 + 60) – 7(9 + 10) + 2(36 – 10)
= 1(75) – 7(19) + 2(26)
= 75 – 133 + 52
= -6
Dz = \(\left|\begin{array}{ccc}
1 & -1 & 7 \\
3 & 4 & 5 \\
2 & -1 & 12
\end{array}\right|\)
= 1(48 + 5) – (-1)(36 – 10) + 7(-3 – 8)
= 1(53)+ 1(26) + 7(-11)
= 53 + 26 – 77
= 2
By Cramer’s Rule,
x = \(\frac{\mathrm{D}_{x}}{\mathrm{D}}=\frac{18}{4}=\frac{9}{2}\)
y = \(\frac{D_{y}}{D}=\frac{-6}{4}=\frac{-3}{2}\)
z = \(\frac{D_{z}}{D}=\frac{2}{4}=\frac{1}{2}\)
∴ x = \(\frac{9}{2}\), y = \(\frac{-3}{2}\) and z = \(\frac{1}{2}\) are the solutions of the given equations.

Question 6.
Find the value(s) of k, if the following equations are consistent.
(i) 3x + y – 2 = 0, kx + 2y – 3 = 0 and 2x – y = 3
Solution:
Given equations are
3x + y – 2 = 0
kx + 2y – 3 = 0
2x – y = 3 i.e. 2x – y – 3 = 0
Since, these equations are consistent.
∴ \(\left|\begin{array}{rrr}
3 & 1 & -2 \\
k & 2 & -3 \\
2 & -1 & -3
\end{array}\right|=0\)
∴ 3(-6 – 3) – 1(-3k + 6) – 2(-k – 4) = 0
∴ 3(-9) – 1 (-3k + 6) – 2(-k – 4) = 0
∴ -27 + 3k – 6 + 2k + 8 = 0
∴ 5k – 25 = 0
∴ k = 5
(ii) kx + 3y + 4 = 0, x + ky + 3 = 0, 3x + 4y + 5 = 0
Solution:
Given equations are
kx + 3y + 4 = 0
x + ky + 3 = 0
3x + 4y + 5 = 0
Since, these equations are consistent.
∴ \(\left|\begin{array}{lll}
\mathrm{k} & 3 & 4 \\
1 & \mathrm{k} & 3 \\
3 & 4 & 5
\end{array}\right|=0\)
∴ k(5k – 12) – 3(5 – 9) + 4(4 – 3k) = 0
∴ 5k2 – 12k + 12 + 16 – 12k = 0
∴ 5k2 – 24k + 28 = 0
∴ 5k2 – 10k – 14k + 28 = 0
∴ 5k(k – 2) – 14(k – 2) = 0
∴ (k – 2) (5k – 14) = 0
∴ k – 2 = 0 or 5k – 14 = 0
∴ k = 2 or k = \(\frac{14}{5}\)
Question 7.
Find the area of triangles whose vertices are
(i) A(-1, 2), B(2, 4), C(0, 0)
Solution:
Here, A(x1, y1) ≡ A(-1, 2), B(x2, y2) ≡ B(2, 4), C(x3, y3) ≡ C(0, 0)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ A(∆ABC) = \(\frac{1}{2}\left|\begin{array}{ccc}
-1 & 2 & 1 \\
2 & 4 & 1 \\
0 & 0 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [-1(4 – 0) – 2(2 – 0) + 1(0 – 0)]
= \(\frac{1}{2}\) (-4 – 4)
= \(\frac{1}{2}\) (-8)
= -4
Since, area cannot be negative.
∴ A(∆ABC) = 4 sq.units
(ii) P(3, 6), Q(-1, 3), R(2, -1)
Solution:
Here, P(x1, y1) ≡ P(3, 6), Q(x2, y2) ≡ Q(-1, 3), R(x3, y3) ≡ R(2, -1)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
A(∆PQR) = \(\frac{1}{2}\left|\begin{array}{ccc}
3 & 6 & 1 \\
-1 & 3 & 1 \\
2 & -1 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [3(3 + 1) – 6(-1 – 2) + 1(1 – 6)]
= \(\frac{1}{2}\) [3(4) – 6(-3) + 1(-5)]
= \(\frac{1}{2}\) (12 + 18 – 5)
∴ A(∆PQR) = \(\frac{25}{2}\) sq.units

(iii) L(1, 1), M(-2, 2), N(5, 4)
Solution:
Here, L(x1, y1) ≡ L(1, 1), M(x2, y2) ≡ M(-2, 2), N(x3, y3) ≡ N(5, 4)
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
A(∆LMN) = \(\frac{1}{2}\left|\begin{array}{rrr}
1 & 1 & 1 \\
-2 & 2 & 1 \\
5 & 4 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [1(2 – 4) -1(-2 – 5) + 1(-8 – 10)]
= \(\frac{1}{2}\) [1(-2) – 1(-7) + 1(-18)]
= \(\frac{1}{2}\) (-2 + 7 – 18)
= \(\frac{-13}{2}\)
Since, area cannot be negative.
∴ A(∆LMN) = \(\frac{13}{2}\) sq.units
Question 8.
Find the value of k,
(i) if the area of ∆PQR is 4 square units and vertices are P(k, 0), Q(4, 0), R(0, 2).
Solution:
Here, P(x1, y1) ≡ P(k, 0), Q(x2, y2) ≡ Q(4, 0), R(x3, y3) ≡ R(0, 2)
A(∆PQR) = 4 sq.units
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ ±4 = \(\frac{1}{2}\left|\begin{array}{lll}
k & 0 & 1 \\
4 & 0 & 1 \\
0 & 2 & 1
\end{array}\right|\)
∴ ±4 = \(\frac{1}{2}\) [k(0 – 2) – 0 + 1(8 – 0)]
∴ ±8 = -2k + 8
∴ 8 = -2k + 8 or -8 = -2k + 8
∴ -2k = 0 or 2k = 16
∴ k = 0 or k = 8

(ii) if area of ∆LMN is \(\frac{33}{2}\) square units and vertices are L(3, -5), M(-2, k), N(1, 4).
Solution:
Here, L(x1, y1) ≡ L(3, -5), M(x2, y2) ≡ M(-2, k), N(x3, y3) ≡ N(1, 4)
A(∆LMN) = \(\frac{33}{2}\) sq.units
Area of a triangle = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
∴ \(\pm \frac{33}{2}=\frac{1}{2}\left|\begin{array}{ccc}
3 & -5 & 1 \\
-2 & \mathrm{k} & 1 \\
1 & 4 & 1
\end{array}\right|\)
∴ ±\(\frac{33}{2}\) = \(\frac{1}{2}\) [3(k – 4) – (-5) (-2 – 1) + 1(-8 – k)]
∴ ±33 = 3k – 12 – 15 – 8 – k
∴ 33 = 2k – 35
∴ 2k – 35 = 33 or 2k – 35 = -33
∴ 2k = 68 or 2k = 2
∴ k = 34 or k = 1