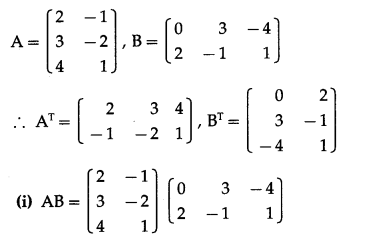Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf
Chapter 2 Matrices Ex 2.4 Questions and Answers.
Question 1.
Find AT, if
(i) A = \(\left[\begin{array}{cc}
1 & 3 \\
-4 & 5
\end{array}\right]\)
(ii) A = \(\left[\begin{array}{ccc}
2 & -6 & 1 \\
-4 & 0 & 5
\end{array}\right]\)
Solution:

Question 2.
If A = [aij]3×3 where aij = 2(i – j). Find A and AT. State whether A and AT both are symmetric or skew-symmetric matrices.
Solution:
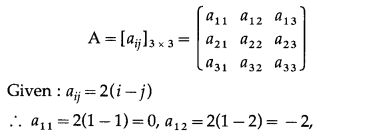
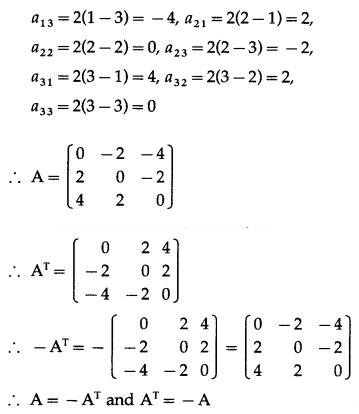
Hence, A and AT are both skew-symmetric matrices.

Question 3.
If A = \(\left[\begin{array}{cc}
5 & -3 \\
4 & -3 \\
-2 & 1
\end{array}\right]\), prove that (AT)T = A.
Solution:
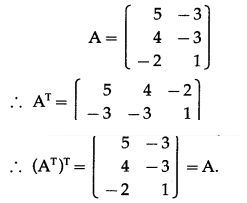
Question 4.
If A = \(\left[\begin{array}{ccc}
1 & 2 & -5 \\
2 & -3 & 4 \\
-5 & 4 & 9
\end{array}\right]\), prove that AT = A.
Solution:
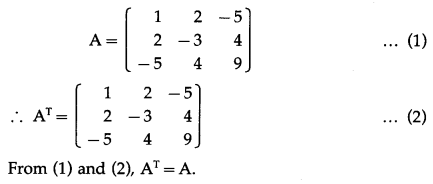
Question 5.
If A = \(\left[\begin{array}{cc}
2 & -3 \\
5 & -4 \\
-6 & 1
\end{array}\right]\), B = \(\left[\begin{array}{cc}
2 & 1 \\
4 & -1 \\
-3 & 3
\end{array}\right]\), C = \(\left[\begin{array}{cc}
1 & 2 \\
-1 & 4 \\
-2 & 3
\end{array}\right]\), then show that
(i) (A + B)T = AT + BT
(ii) (A – C)T = AT – CT
Solution:



Question 6.
If A = \(\left[\begin{array}{cc}
5 & 4 \\
-2 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
-1 & 3 \\
4 & -1
\end{array}\right]\), then find CT, such that 3A – 2B + C = I, where I is the unit matrix of order 2.
Solution:
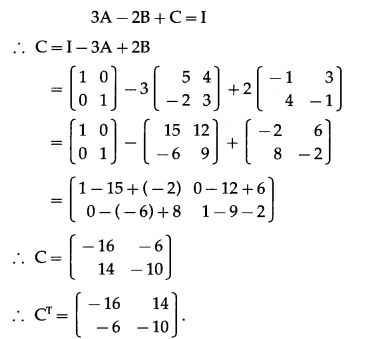
Question 7.
If A = \(\left[\begin{array}{ccc}
7 & 3 & 0 \\
0 & 4 & -2
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
0 & -2 & 3 \\
2 & 1 & -4
\end{array}\right]\), then find
(i) AT + 4BT
(ii) 5AT – 5BT
Solution:
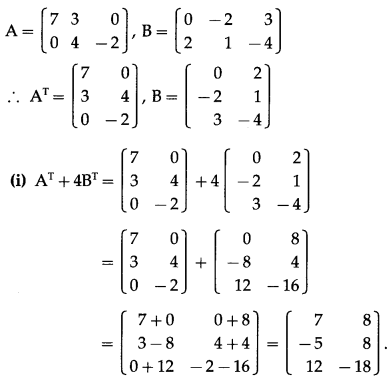
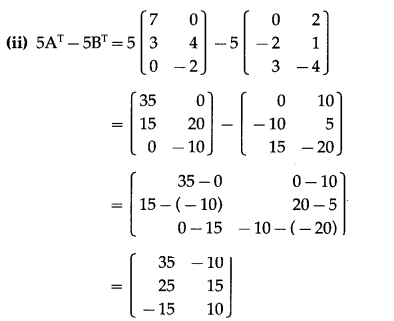
Question 8.
If A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
3 & 1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{lll}
2 & 1 & -4 \\
3 & 5 & -2
\end{array}\right]\) and C = \(\left[\begin{array}{ccc}
0 & 2 & 3 \\
-1 & -1 & 0
\end{array}\right]\), verify that (A + 2B + 3C)T = AT + 2BT + 3CT
Solution:
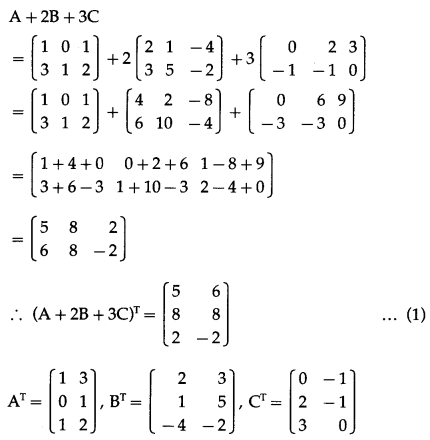


Question 9.
If A = \(\left[\begin{array}{ccc}
-1 & 2 & 1 \\
-3 & 2 & -3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
2 & 1 \\
-3 & 2 \\
-1 & 3
\end{array}\right]\), prove that (A + BT)T = AT + B.
Solution:
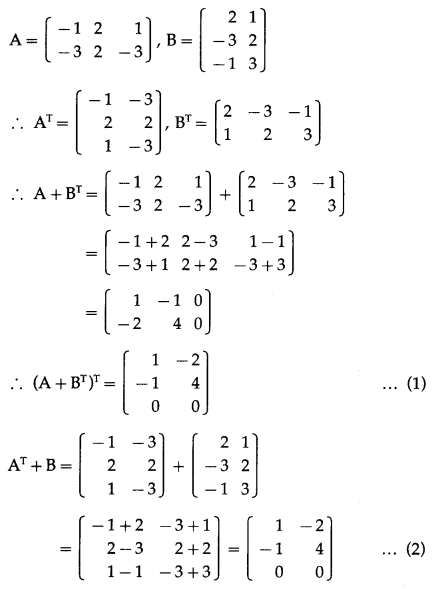
From (1) and (2),
(A + BT)T = AT + B.
Question 10.
Prove that A + AT is symmetric and A – AT is a skew-symmetric matrix, where
(i) A = \(\left[\begin{array}{ccc}
1 & 2 & 4 \\
3 & 2 & 1 \\
-2 & -3 & 2
\end{array}\right]\)
(ii) A = \(\left[\begin{array}{ccc}
5 & 2 & -4 \\
3 & -7 & 2 \\
4 & -5 & -3
\end{array}\right]\)
Solution:

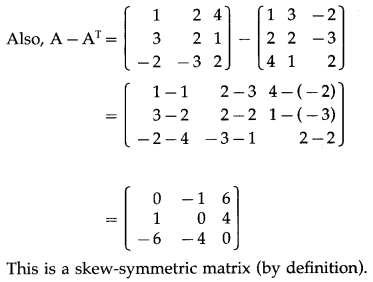
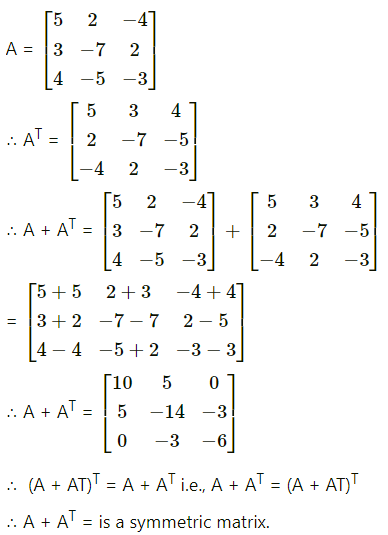
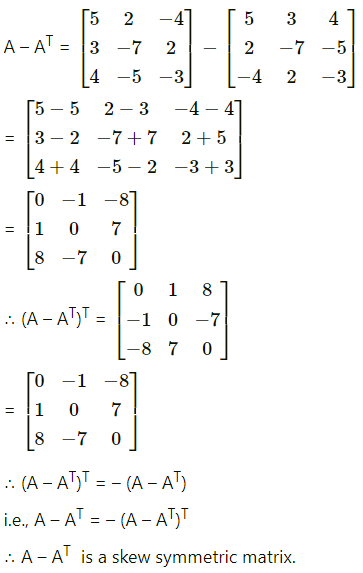

Question 11.
Express each of the following matrix as the sum of a symmetric and a skew-symmetric matrix:
(i) \(\left[\begin{array}{ll}
4 & -2 \\
3 & -5
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
3 & 3 & -1 \\
-2 & -2 & 1 \\
-4 & -5 & 2
\end{array}\right]\)
Solution:
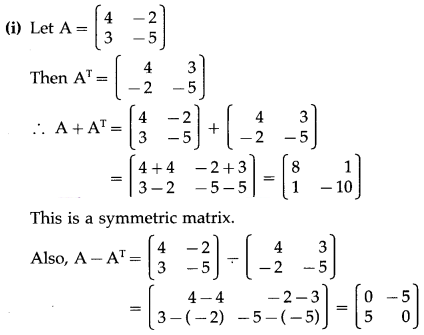
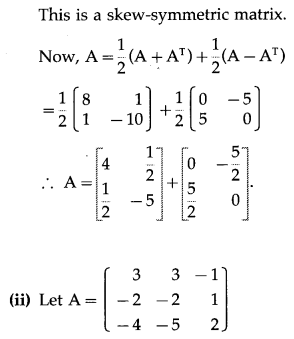



Question 12.
If A = \(\left[\begin{array}{cc}
2 & -1 \\
3 & -2 \\
4 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
0 & 3 & -4 \\
2 & -1 & 1
\end{array}\right]\), verify that
(i) (AB)T = BTAT
(ii) (BA)T = ATBT
Solution:
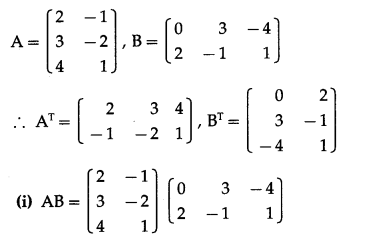


Chapter 2 Matrices Ex 2.4 Questions and Answers.
Question 1.
Find AT, if
(i) A = \(\left[\begin{array}{cc}
1 & 3 \\
-4 & 5
\end{array}\right]\)
(ii) A = \(\left[\begin{array}{ccc}
2 & -6 & 1 \\
-4 & 0 & 5
\end{array}\right]\)
Solution:

Question 2.
If A = [aij]3×3 where aij = 2(i – j). Find A and AT. State whether A and AT both are symmetric or skew-symmetric matrices.
Solution:
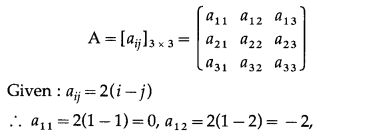
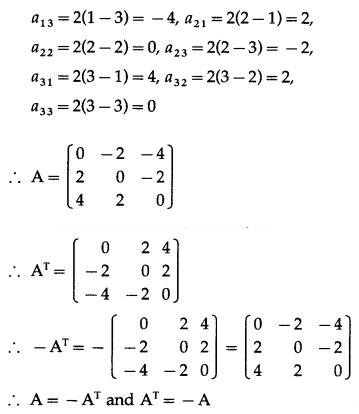
Hence, A and AT are both skew-symmetric matrices.

Question 3.
If A = \(\left[\begin{array}{cc}
5 & -3 \\
4 & -3 \\
-2 & 1
\end{array}\right]\), prove that (AT)T = A.
Solution:
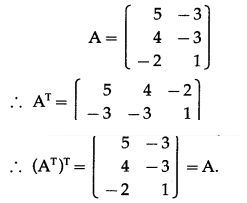
Question 4.
If A = \(\left[\begin{array}{ccc}
1 & 2 & -5 \\
2 & -3 & 4 \\
-5 & 4 & 9
\end{array}\right]\), prove that AT = A.
Solution:
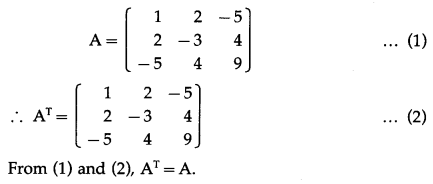
Question 5.
If A = \(\left[\begin{array}{cc}
2 & -3 \\
5 & -4 \\
-6 & 1
\end{array}\right]\), B = \(\left[\begin{array}{cc}
2 & 1 \\
4 & -1 \\
-3 & 3
\end{array}\right]\), C = \(\left[\begin{array}{cc}
1 & 2 \\
-1 & 4 \\
-2 & 3
\end{array}\right]\), then show that
(i) (A + B)T = AT + BT
(ii) (A – C)T = AT – CT
Solution:



Question 6.
If A = \(\left[\begin{array}{cc}
5 & 4 \\
-2 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
-1 & 3 \\
4 & -1
\end{array}\right]\), then find CT, such that 3A – 2B + C = I, where I is the unit matrix of order 2.
Solution:
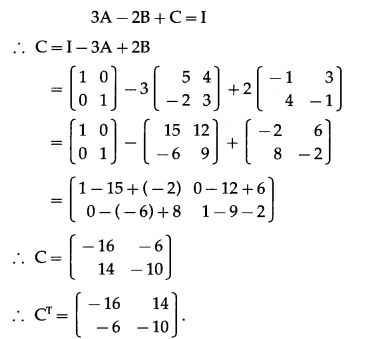
Question 7.
If A = \(\left[\begin{array}{ccc}
7 & 3 & 0 \\
0 & 4 & -2
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
0 & -2 & 3 \\
2 & 1 & -4
\end{array}\right]\), then find
(i) AT + 4BT
(ii) 5AT – 5BT
Solution:
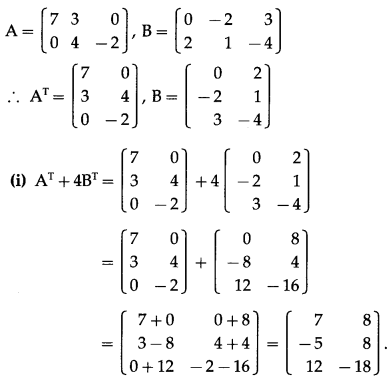
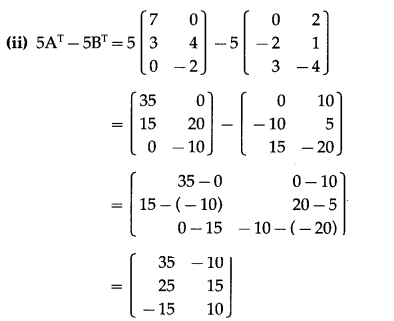
Question 8.
If A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
3 & 1 & 2
\end{array}\right]\), B = \(\left[\begin{array}{lll}
2 & 1 & -4 \\
3 & 5 & -2
\end{array}\right]\) and C = \(\left[\begin{array}{ccc}
0 & 2 & 3 \\
-1 & -1 & 0
\end{array}\right]\), verify that (A + 2B + 3C)T = AT + 2BT + 3CT
Solution:
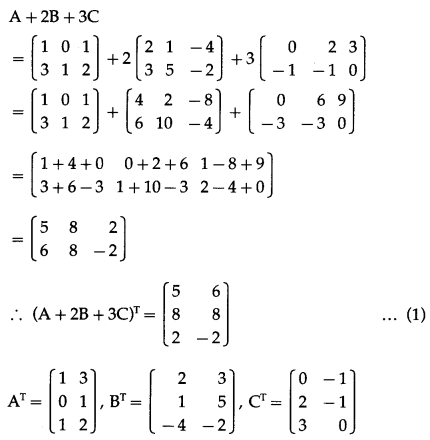


Question 9.
If A = \(\left[\begin{array}{ccc}
-1 & 2 & 1 \\
-3 & 2 & -3
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
2 & 1 \\
-3 & 2 \\
-1 & 3
\end{array}\right]\), prove that (A + BT)T = AT + B.
Solution:
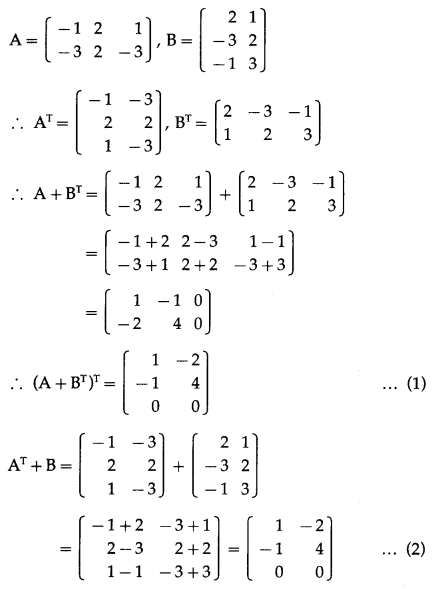
From (1) and (2),
(A + BT)T = AT + B.
Question 10.
Prove that A + AT is symmetric and A – AT is a skew-symmetric matrix, where
(i) A = \(\left[\begin{array}{ccc}
1 & 2 & 4 \\
3 & 2 & 1 \\
-2 & -3 & 2
\end{array}\right]\)
(ii) A = \(\left[\begin{array}{ccc}
5 & 2 & -4 \\
3 & -7 & 2 \\
4 & -5 & -3
\end{array}\right]\)
Solution:

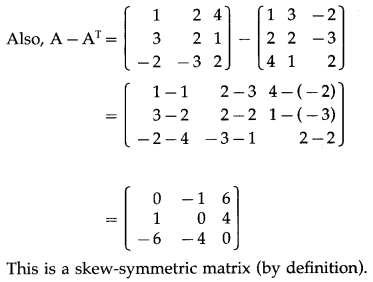
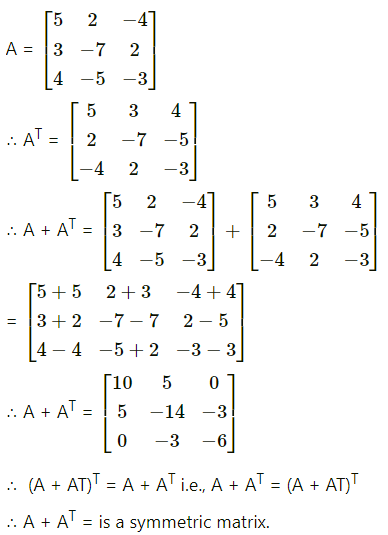
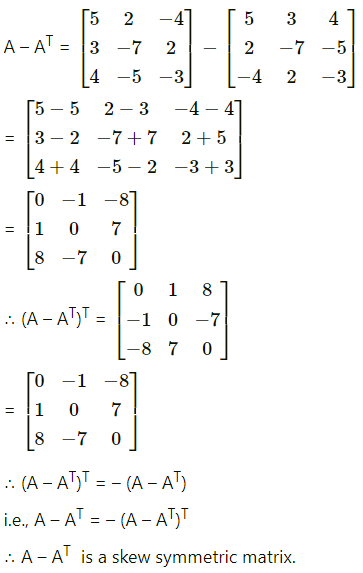

Question 11.
Express each of the following matrix as the sum of a symmetric and a skew-symmetric matrix:
(i) \(\left[\begin{array}{ll}
4 & -2 \\
3 & -5
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
3 & 3 & -1 \\
-2 & -2 & 1 \\
-4 & -5 & 2
\end{array}\right]\)
Solution:
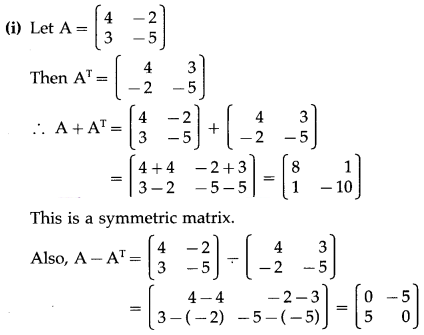
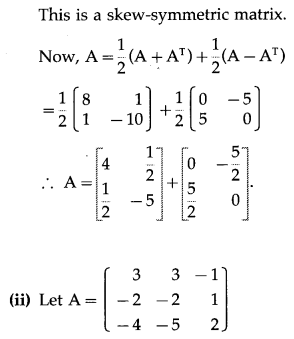



Question 12.
If A = \(\left[\begin{array}{cc}
2 & -1 \\
3 & -2 \\
4 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
0 & 3 & -4 \\
2 & -1 & 1
\end{array}\right]\), verify that
(i) (AB)T = BTAT
(ii) (BA)T = ATBT
Solution: