Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf
Chapter 4 Applications of Derivatives Ex 4.3 Questions and Answers.
Question 1.
Determine the maximum and minimum values of the following functions:
(i) f(x) = 2x3 – 21x2 + 36x – 20
Solution:
f(x) = 2x3 – 21x2 + 36x – 20
∴ f'(x) = \(\frac{d}{d x}\)(2x3 – 21x2 + 36x – 20)
= 2 × 3x2 – 21 × 2x + 36 × 1 – 0
= 6x2 – 42x + 36
and f”(x) = \(\frac{d}{d x}\)(6x2 – 42x + 36)
= 6 × 2x – 42 × 1 + 0
= 12x – 42
f'(x) = 0 gives 6x2 – 42x + 36 = 0.
∴ x2 – 7x + 6 = 0
∴ (x – 1)(x – 6) = 0
∴ the roots of f'(x) = 0 are x1 = 1 and x2 = 6.
For x = 1, f”(1) = 12(1) – 42 = -30 < 0
∴ by the second derivative test,
f has maximum at x = 1 and maximum value of f at x = 1
f(1) = 2(1)3 – 21(1)2 + 36(1) – 20
= 2 – 21 + 36 – 20
= -3
For x = 6, f”(6) = 12(6) – 42 = 30 > 0
∴ by the second derivative test,
f has minimum at x = 6 and minimum value of f at x = 6
f(6) = 2(6)3 – 21(6)2 + 36(6) – 20
= 432 – 756 + 216 – 20
= -128
Hence, the function f has maximum value -3 at x = 1 and minimum value -128 at x = 6.

(ii) f(x) = x . log x
Solution:
f(x) = x . log x
f'(x) = \(\frac{d}{d x}\)(x.log x)
= x.\(\frac{d}{d x}\)(log x) + log x.\(\frac{d}{d x}\)(x)
= x × \(\frac{1}{x}\) + (logx) × 1
= 1 + log x
and f”(x) = \(\frac{d}{d x}\)(1 + logx)
= 0 + \(\frac{1}{x}\)
= \(\frac{1}{x}\)
Now, f'(x) = 0, if 1 + log x = 0
i.e. if log x = -1 = -log e
i.e. if log x = log(e-1) = log \(\frac{1}{e}\)
i.e. if x = \(\frac{1}{e}\)
When x = \(\frac{1}{e}\), f”(x) = \(\frac{1}{(1 / e)}\) = e > 0
∴ by the second derivative test,
f is minimum at x = \(\frac{1}{e}\)
Minimum value of f at x = \(\frac{1}{e}\)
= \(\frac{1}{e}\) log(\(\frac{1}{e}\))
= \(\frac{1}{e}\) log(e-1)
= \(\frac{1}{e}\) (-1) log e
= \(\frac{-1}{e}\) ……..[∵ log e = 1]
Hence, the function f has minimum at x = \(\frac{1}{e}\) and minimum value is \(\frac{-1}{e}\).
(iii) f(x) = x2 + \(\frac{16}{x}\)
Solution:
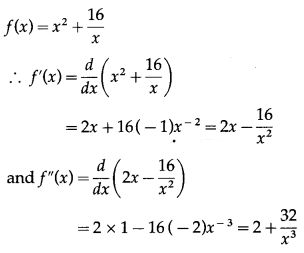
f'(x) = 0 gives 2x – \(\frac{16}{x^{2}}\) = 0
∴ 2x3 – 16 = 0
∴ x3 = 8
∴ x = 2
For x = 2, f”(2) = 2 + \(\frac{32}{(2)^{3}}\) = 6 > 0
∴ by the second derivative test, f has minimum at x = 2 and minimum value of f at x = 2
f(2) = (2)2 + \(\frac{16}{2}\)
= 4 + 8
= 12
Hence, the function f has a minimum at x = 2 and a minimum value is 12.

Question 2.
Divide the number 20 into two parts such that their product is maximum.
Solution:
Let the first part of 20 be x.
Then the second part is 20 – x.
∴ their product = x(20 – x) = 20x – x2 = f(x) …..(Say)
∴ f'(x) = \(\frac{d}{d x}\)(20x – x2)
= 20 × 1 – 2x
= 20 – 2x
and f”(x) = \(\frac{d}{d x}\)(20 – 2x)
= 0 – 2 × 1
= -2
The root of the equation f'(x) = 0
i.e. 20 – 2x = 0 is x = 10
and f”(10) = -2 < 0
∴ by the second derivative test, f is maximum at x = 10.
Hence, the required parts of 20 are 10 and 10.
Question 3.
A metal wire of 36 cm long is bent to form a rectangle. Find its dimensions where its area is maximum.
Solution:
Let x cm and y cm be the length and breadth of the rectangle.
Then its perimeter is 2(x + y) = 36
∴ x + y = 18
∴ y = 18 – x
Area of the rectangle = xy = x(18 – x)
Let f(x) = x(18 – x) = 18x – x2
Then f'(x) = \(\frac{d}{d x}\)(18x – x2)
= 18 × 1 – 2x
= 18 – 2x
and f”(x) = \(\frac{d}{d x}\)(18 – 2x)
= 0 – 2 × 1
= -2
Now, f(x) = 0, if 18 – 2x = 0
i.e. if x = 9
and f”(9) = -2 < 0
∴ by the second derivative test, f has maximum value at x = 9
When x = 9, y = 18 – 9 = 9
Hence, the rectangle is a square of side 9 cm.

Question 4.
The total cost of producing x units is ₹(x2 + 60x + 50) and the price is ₹(180 – x) per unit. For what units is the profit maximum?
Solution:
Let the number of units sold be x.
Then profit = S.P. – C.P.
∴ P(x) = (180 – x)x – (x2 + 60x + 50)
∴ P(x) = 180x – x2 – x2 – 60x – 50
∴ P(x) = 120x – 2x2 – 50
P'(x) = \(\frac{d}{d x}\)(120x – 2x2 – 50)
= 120 × 1 – 2 × 2x – 0
= 120 – 4x
and P”(x) = \(\frac{d}{d x}\)(120 – 4x)
= 0 – 4 × 1
= -4
P'(x) = 0 if 120 – 4x = 0
i.e. if x = 30 and P”(30) = -4 < 0
∴ by the second derivative test, P(x) is maximum when x = 30.
Hence, the number of units sold for maximum profit is 30.
Chapter 4 Applications of Derivatives Ex 4.3 Questions and Answers.
Question 1.
Determine the maximum and minimum values of the following functions:
(i) f(x) = 2x3 – 21x2 + 36x – 20
Solution:
f(x) = 2x3 – 21x2 + 36x – 20
∴ f'(x) = \(\frac{d}{d x}\)(2x3 – 21x2 + 36x – 20)
= 2 × 3x2 – 21 × 2x + 36 × 1 – 0
= 6x2 – 42x + 36
and f”(x) = \(\frac{d}{d x}\)(6x2 – 42x + 36)
= 6 × 2x – 42 × 1 + 0
= 12x – 42
f'(x) = 0 gives 6x2 – 42x + 36 = 0.
∴ x2 – 7x + 6 = 0
∴ (x – 1)(x – 6) = 0
∴ the roots of f'(x) = 0 are x1 = 1 and x2 = 6.
For x = 1, f”(1) = 12(1) – 42 = -30 < 0
∴ by the second derivative test,
f has maximum at x = 1 and maximum value of f at x = 1
f(1) = 2(1)3 – 21(1)2 + 36(1) – 20
= 2 – 21 + 36 – 20
= -3
For x = 6, f”(6) = 12(6) – 42 = 30 > 0
∴ by the second derivative test,
f has minimum at x = 6 and minimum value of f at x = 6
f(6) = 2(6)3 – 21(6)2 + 36(6) – 20
= 432 – 756 + 216 – 20
= -128
Hence, the function f has maximum value -3 at x = 1 and minimum value -128 at x = 6.

(ii) f(x) = x . log x
Solution:
f(x) = x . log x
f'(x) = \(\frac{d}{d x}\)(x.log x)
= x.\(\frac{d}{d x}\)(log x) + log x.\(\frac{d}{d x}\)(x)
= x × \(\frac{1}{x}\) + (logx) × 1
= 1 + log x
and f”(x) = \(\frac{d}{d x}\)(1 + logx)
= 0 + \(\frac{1}{x}\)
= \(\frac{1}{x}\)
Now, f'(x) = 0, if 1 + log x = 0
i.e. if log x = -1 = -log e
i.e. if log x = log(e-1) = log \(\frac{1}{e}\)
i.e. if x = \(\frac{1}{e}\)
When x = \(\frac{1}{e}\), f”(x) = \(\frac{1}{(1 / e)}\) = e > 0
∴ by the second derivative test,
f is minimum at x = \(\frac{1}{e}\)
Minimum value of f at x = \(\frac{1}{e}\)
= \(\frac{1}{e}\) log(\(\frac{1}{e}\))
= \(\frac{1}{e}\) log(e-1)
= \(\frac{1}{e}\) (-1) log e
= \(\frac{-1}{e}\) ……..[∵ log e = 1]
Hence, the function f has minimum at x = \(\frac{1}{e}\) and minimum value is \(\frac{-1}{e}\).
(iii) f(x) = x2 + \(\frac{16}{x}\)
Solution:
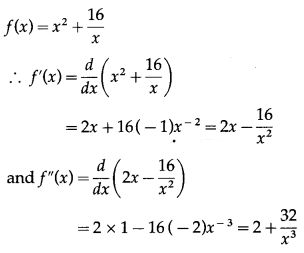
f'(x) = 0 gives 2x – \(\frac{16}{x^{2}}\) = 0
∴ 2x3 – 16 = 0
∴ x3 = 8
∴ x = 2
For x = 2, f”(2) = 2 + \(\frac{32}{(2)^{3}}\) = 6 > 0
∴ by the second derivative test, f has minimum at x = 2 and minimum value of f at x = 2
f(2) = (2)2 + \(\frac{16}{2}\)
= 4 + 8
= 12
Hence, the function f has a minimum at x = 2 and a minimum value is 12.

Question 2.
Divide the number 20 into two parts such that their product is maximum.
Solution:
Let the first part of 20 be x.
Then the second part is 20 – x.
∴ their product = x(20 – x) = 20x – x2 = f(x) …..(Say)
∴ f'(x) = \(\frac{d}{d x}\)(20x – x2)
= 20 × 1 – 2x
= 20 – 2x
and f”(x) = \(\frac{d}{d x}\)(20 – 2x)
= 0 – 2 × 1
= -2
The root of the equation f'(x) = 0
i.e. 20 – 2x = 0 is x = 10
and f”(10) = -2 < 0
∴ by the second derivative test, f is maximum at x = 10.
Hence, the required parts of 20 are 10 and 10.
Question 3.
A metal wire of 36 cm long is bent to form a rectangle. Find its dimensions where its area is maximum.
Solution:
Let x cm and y cm be the length and breadth of the rectangle.
Then its perimeter is 2(x + y) = 36
∴ x + y = 18
∴ y = 18 – x
Area of the rectangle = xy = x(18 – x)
Let f(x) = x(18 – x) = 18x – x2
Then f'(x) = \(\frac{d}{d x}\)(18x – x2)
= 18 × 1 – 2x
= 18 – 2x
and f”(x) = \(\frac{d}{d x}\)(18 – 2x)
= 0 – 2 × 1
= -2
Now, f(x) = 0, if 18 – 2x = 0
i.e. if x = 9
and f”(9) = -2 < 0
∴ by the second derivative test, f has maximum value at x = 9
When x = 9, y = 18 – 9 = 9
Hence, the rectangle is a square of side 9 cm.

Question 4.
The total cost of producing x units is ₹(x2 + 60x + 50) and the price is ₹(180 – x) per unit. For what units is the profit maximum?
Solution:
Let the number of units sold be x.
Then profit = S.P. – C.P.
∴ P(x) = (180 – x)x – (x2 + 60x + 50)
∴ P(x) = 180x – x2 – x2 – 60x – 50
∴ P(x) = 120x – 2x2 – 50
P'(x) = \(\frac{d}{d x}\)(120x – 2x2 – 50)
= 120 × 1 – 2 × 2x – 0
= 120 – 4x
and P”(x) = \(\frac{d}{d x}\)(120 – 4x)
= 0 – 4 × 1
= -4
P'(x) = 0 if 120 – 4x = 0
i.e. if x = 30 and P”(30) = -4 < 0
∴ by the second derivative test, P(x) is maximum when x = 30.
Hence, the number of units sold for maximum profit is 30.