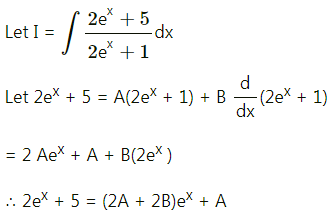Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf
Chapter 5 Integration Ex 5.3 Questions and Answers.
Evaluate the following:
Question 1.
\(\int \frac{3 e^{2 t}+5}{4 e^{2 t}-5} d t\)
Solution:
Let I = \(\int \frac{3 e^{2 t}+5}{4 e^{2 t}-5} d t\)
Put, Numerator = A(Denominator) + B[\(\frac{d}{d x}\)(Denominator)]
∴ 3e2t + 5 = A(4e2t – 5) + B[\(\frac{d}{d t}\)(4e2t – 5)]
∴ 3e2t + 5 = A(4e2t – 5) + B[4e2t × 2 – 0]
∴ 3e2t + 5 = (4A + 8B) e2t – 5A
Equating the coefficient of e2t and constant on both sides, we get
4A + 8B = 3
and -5A = 5
∴ A = -1
∴ from (1), 4(-1) + 8B = 3
∴ 8B = 7
∴ B = \(\frac{7}{8}\)
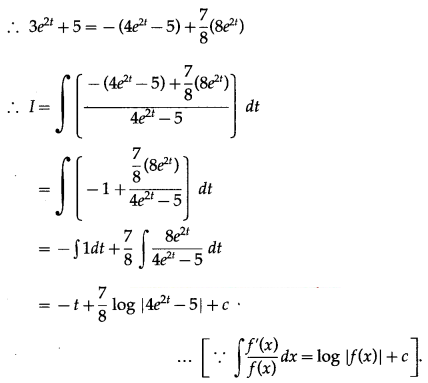

Question 2.
\(\int \frac{20-12 e^{x}}{3 e^{x}-4} d x\)
Solution:
Let I = \(\int \frac{20-12 e^{x}}{3 e^{x}-4} d x\)
Put, Numerator = A (Denominator) + B[\(\frac{d}{d x}\)(Denominator)]
∴ 20 – 12ex = A(3ex – 4) + B[\(\frac{d}{d x}\)(3ex – 4)]
∴ 20 – 12ex = A(3ex – 4) + B(3ex – 0)
∴ 20 – 12ex = (3A + 3B)ex – 4A
Equating the coefficient of ex and constant on both sides, we get
3A + 3B = -12 ……(1)
and -4A = 20
∴ A = -5
from (1), 3(-5) + 3B = -12
∴ 3B = 3
∴ B = 1
∴ 20 – 12ex = -5(3ex – 4) + (3ex)
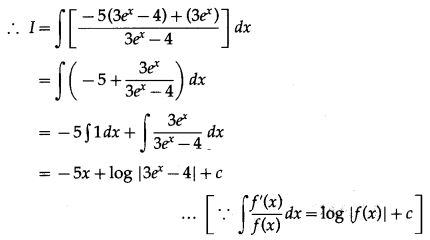
Question 3.
\(\int \frac{3 e^{x}+4}{2 e^{x}-8} d x\)
Solution:
Let I = \(\int \frac{3 e^{x}+4}{2 e^{x}-8} d x\)
Put, Numerator = A (Denominator) + B[\(\frac{d}{d x}\)(Denominator)]
∴ 3ex + 4 = A(2ex – 8) + B[\(\frac{d}{d x}\)(2ex – 8)]
∴ 3ex + 4 = A(2ex – 8) + B(2ex – 0)
∴ 3ex + 4 = (2A + 2B)ex – 8A
Equating the coefficient of ex and constant on both sides, we get
2A + 2B = 3 ……..(1)
and -8A = 4
∴ A = \(-\frac{1}{2}\)
∴ from (1), 2(\(-\frac{1}{2}\)) + 2B = 3
∴ 2B = 4
∴ B = 2
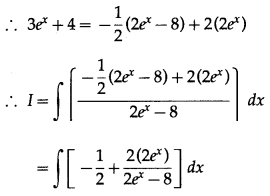
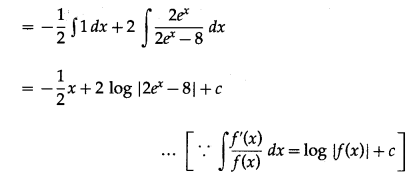

Question 4.
\(\int \frac{2 e^{x}+5}{2 e^{x}+1} d x\)
Solution:
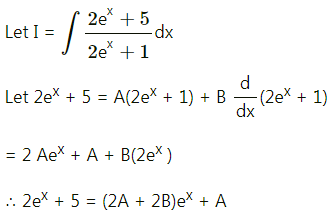

Chapter 5 Integration Ex 5.3 Questions and Answers.
Evaluate the following:
Question 1.
\(\int \frac{3 e^{2 t}+5}{4 e^{2 t}-5} d t\)
Solution:
Let I = \(\int \frac{3 e^{2 t}+5}{4 e^{2 t}-5} d t\)
Put, Numerator = A(Denominator) + B[\(\frac{d}{d x}\)(Denominator)]
∴ 3e2t + 5 = A(4e2t – 5) + B[\(\frac{d}{d t}\)(4e2t – 5)]
∴ 3e2t + 5 = A(4e2t – 5) + B[4e2t × 2 – 0]
∴ 3e2t + 5 = (4A + 8B) e2t – 5A
Equating the coefficient of e2t and constant on both sides, we get
4A + 8B = 3
and -5A = 5
∴ A = -1
∴ from (1), 4(-1) + 8B = 3
∴ 8B = 7
∴ B = \(\frac{7}{8}\)
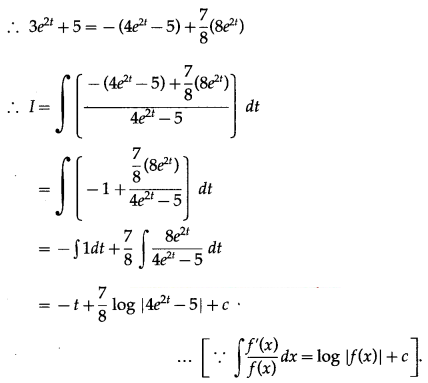

Question 2.
\(\int \frac{20-12 e^{x}}{3 e^{x}-4} d x\)
Solution:
Let I = \(\int \frac{20-12 e^{x}}{3 e^{x}-4} d x\)
Put, Numerator = A (Denominator) + B[\(\frac{d}{d x}\)(Denominator)]
∴ 20 – 12ex = A(3ex – 4) + B[\(\frac{d}{d x}\)(3ex – 4)]
∴ 20 – 12ex = A(3ex – 4) + B(3ex – 0)
∴ 20 – 12ex = (3A + 3B)ex – 4A
Equating the coefficient of ex and constant on both sides, we get
3A + 3B = -12 ……(1)
and -4A = 20
∴ A = -5
from (1), 3(-5) + 3B = -12
∴ 3B = 3
∴ B = 1
∴ 20 – 12ex = -5(3ex – 4) + (3ex)
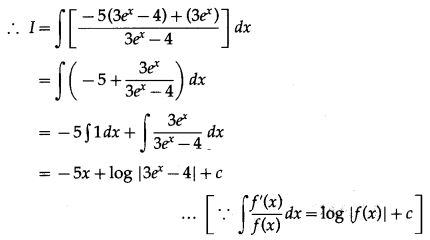
Question 3.
\(\int \frac{3 e^{x}+4}{2 e^{x}-8} d x\)
Solution:
Let I = \(\int \frac{3 e^{x}+4}{2 e^{x}-8} d x\)
Put, Numerator = A (Denominator) + B[\(\frac{d}{d x}\)(Denominator)]
∴ 3ex + 4 = A(2ex – 8) + B[\(\frac{d}{d x}\)(2ex – 8)]
∴ 3ex + 4 = A(2ex – 8) + B(2ex – 0)
∴ 3ex + 4 = (2A + 2B)ex – 8A
Equating the coefficient of ex and constant on both sides, we get
2A + 2B = 3 ……..(1)
and -8A = 4
∴ A = \(-\frac{1}{2}\)
∴ from (1), 2(\(-\frac{1}{2}\)) + 2B = 3
∴ 2B = 4
∴ B = 2
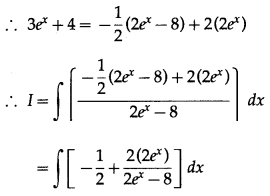
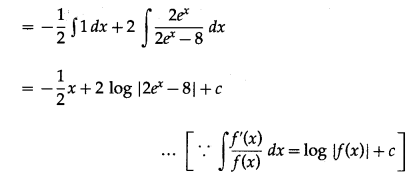

Question 4.
\(\int \frac{2 e^{x}+5}{2 e^{x}+1} d x\)
Solution: