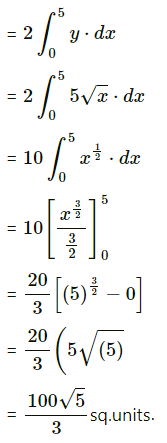Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf
Chapter 7 Application of Definite Integration Miscellaneous Exercise 7 Questions and Answers.
(I) Choose the correct alternatives:
Question 1.
Area of the region bounded by the curve x2 = y, the X-axis and the lines x = 1 and x = 3 is
(a) \(\frac{26}{3}\) sq units
(b) \(\frac{3}{26}\) sq units
(c) 26 sq units
(d) 3 sq units
Answer:
(a) \(\frac{26}{3}\) sq units
Question 2.
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is
(a) 28 sq units
(b) 3 sq unit
(c) \(\frac{28}{3}\) sq units
(d) \(\frac{3}{28}\) sq units
Answer:
(c) \(\frac{28}{3}\) sq units

Question 3.
Area of the region bounded by x2 = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is
(a) 63 sq units
(b) \(\frac{3}{56}\) sq units
(c) \(\frac{56}{3}\) sq units
(d) \(\frac{63}{7}\) sq units
Answer:
(c) \(\frac{56}{3}\) sq units
Question 4.
Area of the region bounded by y = x4, x = 1, x = 5 and the X-axis is
(a) \(\frac{3142}{5}\) sq units
(b) \(\frac{3124}{5}\) sq units
(c) \(\frac{3142}{3}\) sq units
(d) \(\frac{3124}{3}\) sq units
Answer:
(b) \(\frac{3124}{5}\) sq units
Question 5.
Using definite integration area of circle x2 + y2 = 25 is
(a) 5π sq units
(b) 4π sq units
(c) 25π sq units
(d) 25 sq units
Answer:
(c) 25π sq units
(II) Fill in the blanks:
Question 1.
Area of the region bounded by y = x4, x = 1, x = 5 and the X-axis is _________
Answer:
\(\frac{3124}{5}\) sq units
Question 2.
Using definite integration area of the circle x2 + y2 = 49 is ___________
Answer:
49π sq units
Question 3.
Area of the region bounded by x2 = 16y, y = 1, y = 4 and the Y-axis lying in the first quadrant is _________
Answer:
\(\frac{56}{3}\) sq units

Question 4.
The area of the region bounded by the curve x2 = y, the X-axis and the lines x = 3 and x = 9 is _________
Answer:
234 sq units
Question 5.
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is __________
Answer:
\(\frac{28}{3}\) sq units
(III) State whether each of the following is True or False.
Question 1.
The area bounded by the curve x = g(y), Y-axis and bounded between the lines y = c and y = d is given by \(\int_{c}^{d} x d y=\int_{y=c}^{y=d} g(y) d y\)
Answer:
True
Question 2.
The area bounded by two curves y = f(x), y = g(x) and X-axis is \(\left|\int_{a}^{b} f(x) d x-\int_{b}^{a} g(x) d x\right|\)
Answer:
False
Question 3.
The area bounded by the curve y = f(x), X-axis and lines x = a and x = b is \(\left|\int_{a}^{b} f(x) d x\right|\)
Answer:
True

Question 4.
If the curve, under consideration, is below the X-axis, then the area bounded by curve, X-axis, and lines x = a, x = b is positive.
Answer:
False
Question 5.
The area of the portion lying above the X-axis is positive.
Answer:
True
(IV) Solve the following:
Question 1.
Find the area of the region bounded by the curve xy = c2, the X-axis, and the lines x = c, x = 2c.
Solution:
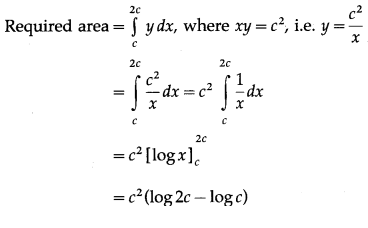
= c2 log(\(\frac{2 c}{c}\))
= c2 . log 2 sq units.
Question 2.
Find the area between the parabolas y2 = 7x and x2 = 7y.
Solution:
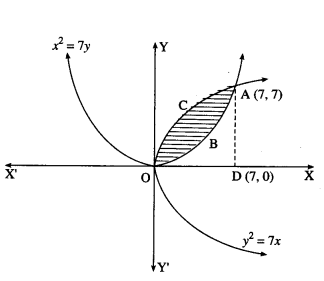
For finding the points of intersection of the two parabolas,
we equate the values of y2 from their equations.
From the equation x2 = 7y, y2 = \(\frac{x^{4}}{49}\)
∴ \(\frac{x^{4}}{49}\) = 7x
∴ x4 = 343x
∴ x4 – 343x = 0
∴ x(x3 – 343) = 0
∴ x = 0 or x3 = 343, i.e. x = 7
When x = 0, y = 0
When x = 7, 7y = 49
∴ y = 7
∴ the points of intersection are O(0, 0) and A(7, 7)
Required area = area of the region OBACO
= (area of the region ODACO) – (area of the region ODABO)
Now, area of the region ODACO = area under the parabola y2 = 7x
i.e. y = √7 √x
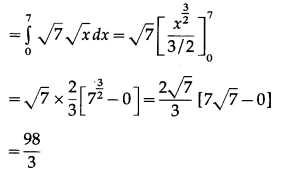
Area of the region ODABO = Area under the parabola
x2 = 7y
i.e. y = \(\frac{x^{2}}{7}\)
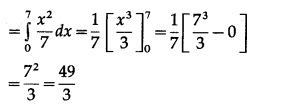
∴ required area = \(\frac{98}{3}-\frac{49}{3}=\frac{49}{3}\) sq units.

Question 3.
Find the area of the region bounded by the curve y = x2 and the line y = 10.
Solution:
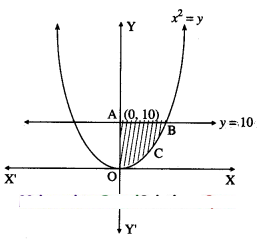
By the symmetry of the parabola,
the required area is twice the area of the region OABCO
Now, the area of the region OABCO
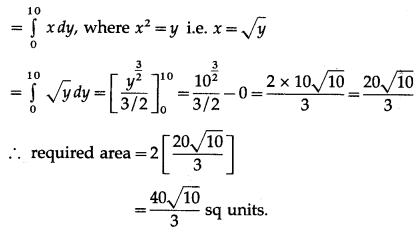
Question 4.
Find the area of the ellipse \(\frac{x^{2}}{16}+\frac{y^{2}}{9}\) = 1.
Solution:
By the symmetry of the ellipse, the required area of the ellipse is 4 times the area of the region OPQO.
For the region OPQO, the limits of integration are x = 0 and x = 4.

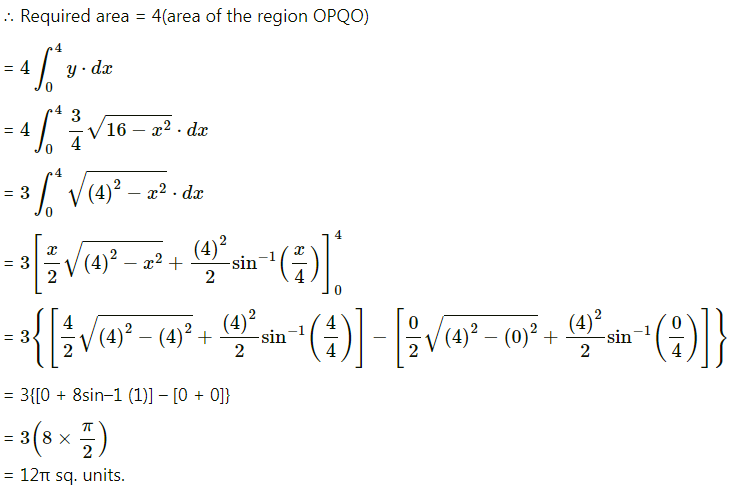
Question 5.
Find the area of the region bounded by y = x2, the X-axis and x = 1, x = 4.
Solution:
Required area = \(\int_{1}^{4} y d x\), where y = x2
= \(\int_{1}^{4} x^{2} d x\)
= \(\left[\frac{x^{3}}{3}\right]_{1}^{4}=\frac{4^{3}}{3}-\frac{1}{3}=\frac{64-1}{3}\)
= 21 sq units.
Question 6.
Find the area of the region bounded by the curve x2 = 25y, y = 1, y = 4, and the Y-axis.
Solution:
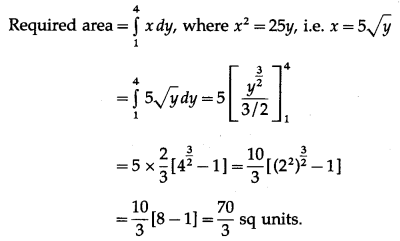

Question 7.
Find the area of the region bounded by the parabola y2 = 25x and the line x = 5.
Solution:
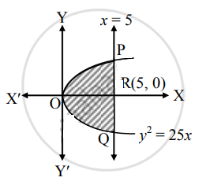
Given the equation of the parabola is y2 = 25x
∴ y = 5√x …… [∵ IIn first quadrant, y > 0]
Required area = area of the region OQRPO
= 2(area of the region ORPO)
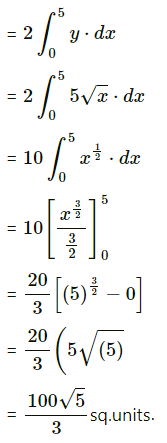
Chapter 7 Application of Definite Integration Miscellaneous Exercise 7 Questions and Answers.
(I) Choose the correct alternatives:
Question 1.
Area of the region bounded by the curve x2 = y, the X-axis and the lines x = 1 and x = 3 is
(a) \(\frac{26}{3}\) sq units
(b) \(\frac{3}{26}\) sq units
(c) 26 sq units
(d) 3 sq units
Answer:
(a) \(\frac{26}{3}\) sq units
Question 2.
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is
(a) 28 sq units
(b) 3 sq unit
(c) \(\frac{28}{3}\) sq units
(d) \(\frac{3}{28}\) sq units
Answer:
(c) \(\frac{28}{3}\) sq units

Question 3.
Area of the region bounded by x2 = 16y, y = 1 and y = 4 and the Y-axis, lying in the first quadrant is
(a) 63 sq units
(b) \(\frac{3}{56}\) sq units
(c) \(\frac{56}{3}\) sq units
(d) \(\frac{63}{7}\) sq units
Answer:
(c) \(\frac{56}{3}\) sq units
Question 4.
Area of the region bounded by y = x4, x = 1, x = 5 and the X-axis is
(a) \(\frac{3142}{5}\) sq units
(b) \(\frac{3124}{5}\) sq units
(c) \(\frac{3142}{3}\) sq units
(d) \(\frac{3124}{3}\) sq units
Answer:
(b) \(\frac{3124}{5}\) sq units
Question 5.
Using definite integration area of circle x2 + y2 = 25 is
(a) 5π sq units
(b) 4π sq units
(c) 25π sq units
(d) 25 sq units
Answer:
(c) 25π sq units
(II) Fill in the blanks:
Question 1.
Area of the region bounded by y = x4, x = 1, x = 5 and the X-axis is _________
Answer:
\(\frac{3124}{5}\) sq units
Question 2.
Using definite integration area of the circle x2 + y2 = 49 is ___________
Answer:
49π sq units
Question 3.
Area of the region bounded by x2 = 16y, y = 1, y = 4 and the Y-axis lying in the first quadrant is _________
Answer:
\(\frac{56}{3}\) sq units

Question 4.
The area of the region bounded by the curve x2 = y, the X-axis and the lines x = 3 and x = 9 is _________
Answer:
234 sq units
Question 5.
The area of the region bounded by y2 = 4x, the X-axis and the lines x = 1 and x = 4 is __________
Answer:
\(\frac{28}{3}\) sq units
(III) State whether each of the following is True or False.
Question 1.
The area bounded by the curve x = g(y), Y-axis and bounded between the lines y = c and y = d is given by \(\int_{c}^{d} x d y=\int_{y=c}^{y=d} g(y) d y\)
Answer:
True
Question 2.
The area bounded by two curves y = f(x), y = g(x) and X-axis is \(\left|\int_{a}^{b} f(x) d x-\int_{b}^{a} g(x) d x\right|\)
Answer:
False
Question 3.
The area bounded by the curve y = f(x), X-axis and lines x = a and x = b is \(\left|\int_{a}^{b} f(x) d x\right|\)
Answer:
True

Question 4.
If the curve, under consideration, is below the X-axis, then the area bounded by curve, X-axis, and lines x = a, x = b is positive.
Answer:
False
Question 5.
The area of the portion lying above the X-axis is positive.
Answer:
True
(IV) Solve the following:
Question 1.
Find the area of the region bounded by the curve xy = c2, the X-axis, and the lines x = c, x = 2c.
Solution:
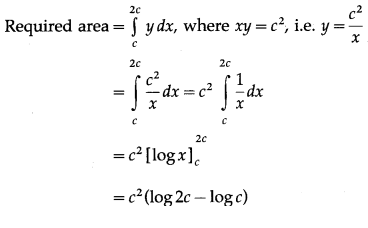
= c2 log(\(\frac{2 c}{c}\))
= c2 . log 2 sq units.
Question 2.
Find the area between the parabolas y2 = 7x and x2 = 7y.
Solution:

For finding the points of intersection of the two parabolas,
we equate the values of y2 from their equations.
From the equation x2 = 7y, y2 = \(\frac{x^{4}}{49}\)
∴ \(\frac{x^{4}}{49}\) = 7x
∴ x4 = 343x
∴ x4 – 343x = 0
∴ x(x3 – 343) = 0
∴ x = 0 or x3 = 343, i.e. x = 7
When x = 0, y = 0
When x = 7, 7y = 49
∴ y = 7
∴ the points of intersection are O(0, 0) and A(7, 7)
Required area = area of the region OBACO
= (area of the region ODACO) – (area of the region ODABO)
Now, area of the region ODACO = area under the parabola y2 = 7x
i.e. y = √7 √x
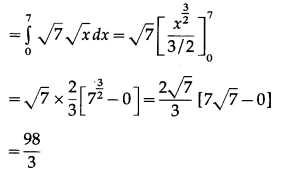
Area of the region ODABO = Area under the parabola
x2 = 7y
i.e. y = \(\frac{x^{2}}{7}\)
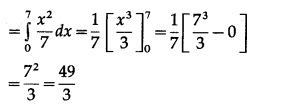
∴ required area = \(\frac{98}{3}-\frac{49}{3}=\frac{49}{3}\) sq units.

Question 3.
Find the area of the region bounded by the curve y = x2 and the line y = 10.
Solution:

By the symmetry of the parabola,
the required area is twice the area of the region OABCO
Now, the area of the region OABCO
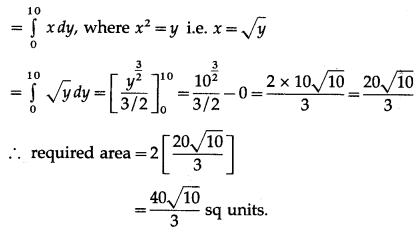
Question 4.
Find the area of the ellipse \(\frac{x^{2}}{16}+\frac{y^{2}}{9}\) = 1.
Solution:
By the symmetry of the ellipse, the required area of the ellipse is 4 times the area of the region OPQO.
For the region OPQO, the limits of integration are x = 0 and x = 4.

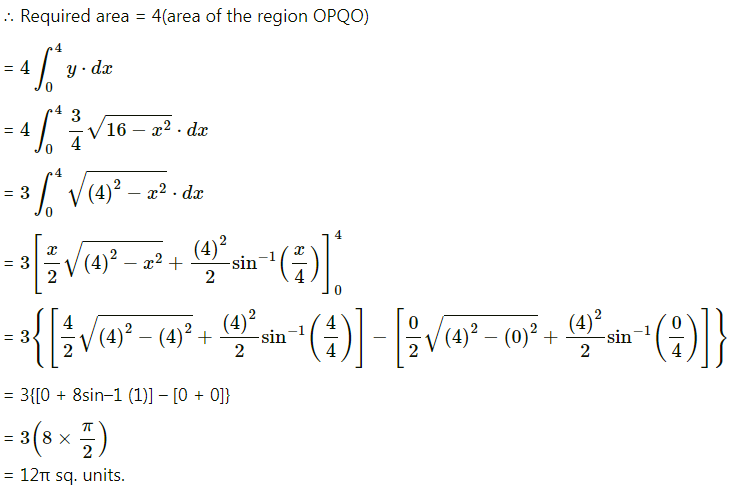
Question 5.
Find the area of the region bounded by y = x2, the X-axis and x = 1, x = 4.
Solution:
Required area = \(\int_{1}^{4} y d x\), where y = x2
= \(\int_{1}^{4} x^{2} d x\)
= \(\left[\frac{x^{3}}{3}\right]_{1}^{4}=\frac{4^{3}}{3}-\frac{1}{3}=\frac{64-1}{3}\)
= 21 sq units.
Question 6.
Find the area of the region bounded by the curve x2 = 25y, y = 1, y = 4, and the Y-axis.
Solution:
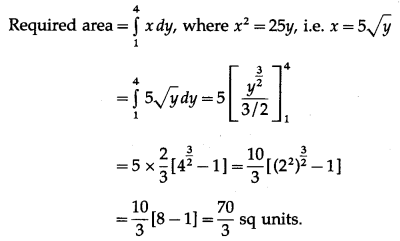

Question 7.
Find the area of the region bounded by the parabola y2 = 25x and the line x = 5.
Solution:

Given the equation of the parabola is y2 = 25x
∴ y = 5√x …… [∵ IIn first quadrant, y > 0]
Required area = area of the region OQRPO
= 2(area of the region ORPO)