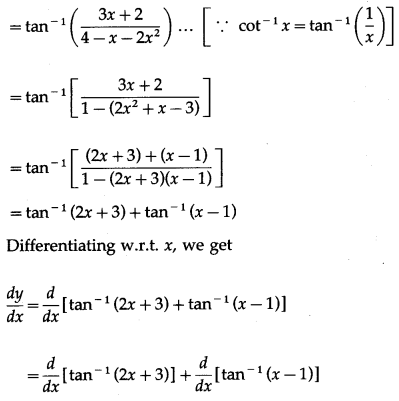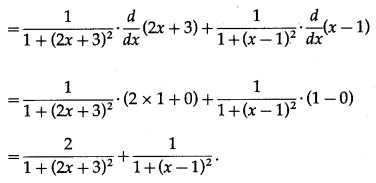Balbharti 12th Maharashtra State Board Maths Solutions Book
Pdf Chapter 1 Differentiation Ex 1.2 Questions and Answers.
Question 1.
Find the derivative of the function y = f(x) using the derivative of the inverse function x = f-1( y) in the following
(i) y = \(\sqrt {x}\)
Solution:
y = \(\sqrt {x}\) … (1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
y2 = x ∴ x = y2
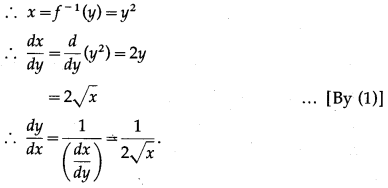
(ii) y = \(\sqrt{2-\sqrt{x}}\)
Solution:
y = \(\sqrt{2-\sqrt{x}}\) …(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
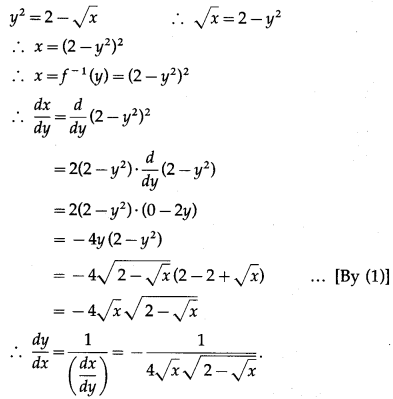
(iii) y = \(\sqrt[3]{x-2}\)
Solution:
y = \(\sqrt[3]{x-2}\) ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
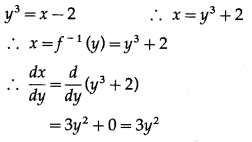
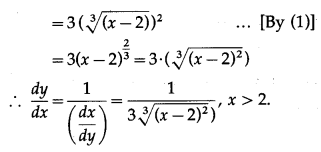

(iv) y = log (2x – 1)
Solution:
y = log (2x – 1) …(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
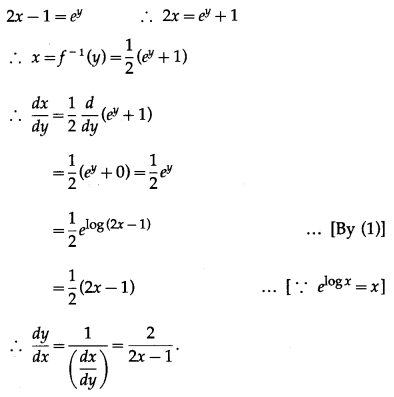
(v) y = 2x + 3
Solution:
y = 2x + 3 ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
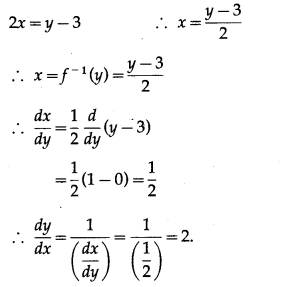
(vi) y = ex – 3
Solution:
y = ex – 3 ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
ex = y + 3
∴ x = log(y + 3)
∴ x = f-1(y) = log(y + 3)
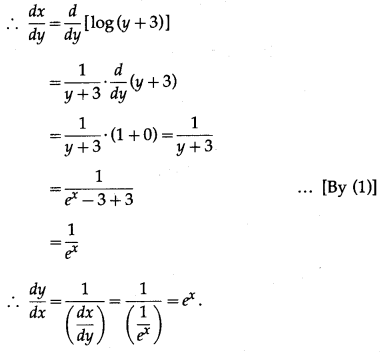

(vii) y = e2x – 3
Solution:
y = e2x – 3 ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
2x – 3 = log y ∴ 2x = log y + 3

(viii) y = log2\(\left(\frac{x}{2}\right)\)
Solution:
y = log2\(\left(\frac{x}{2}\right)\) …(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
\(\frac{x}{2}\) = 2y ∴ x = 2∙2y = 2y+1
∴ x = f-1(y) = 2y+1
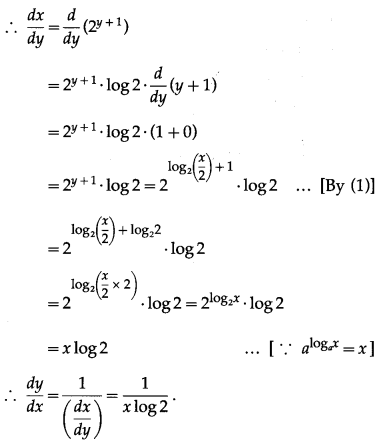
Question 2.
Find the derivative of the inverse function of
the following
(i) y = x2·ex
Solution:
y = x2·ex
Differentiating w.r.t. x, we get


(ii) y = x cos x
Solution:
y = x cos x
Differentiating w.r.t. x, we get
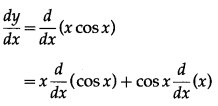
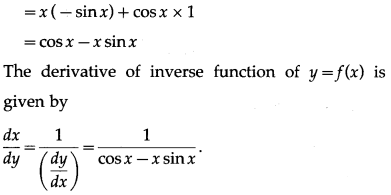
(iii) y = x·7x
Solution:
y = x·7x
Differentiating w.r.t. x, we get

(iv) y = x2 + logx
Solution:
y = x2 + logx
Differentiating w.r.t. x, we get


(v) y = x logx
Solution:
y = x logx
Differentiating w.r.t. x, we get
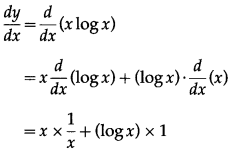

Question 3.
Find the derivative of the inverse of the following functions, and also fid their value at the points indicated against them.
(i) y = x5 + 2x3 + 3x, at x = 1
Solution:
y = x5 + 2x3 + 3x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(x5 + 2x3 + 3x)
= 5x4 + 2 × 3x2 + 3 × 1
= 5x4 + 6x2 + 3
The derivative of inverse function of y = f(x) is given by
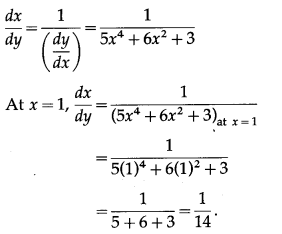
(ii) y = ex + 3x + 2, at x = 0
Solution:
y = ex + 3x + 2
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(ex + 3x + 2)
The derivative of inverse function of y = f(x) is given by
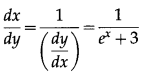
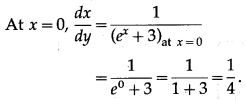

(iii) y = 3x2 + 2 log x3, at x = 1
Solution:
y = 3x2 + 2 log x3
= 3x2 + 6 log x
Differentiating w.r.t. x, we get
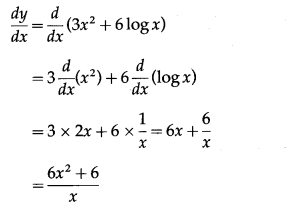
The derivative of inverse function of y = f(x) is given by
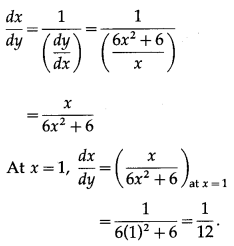
(iv) y = sin (x – 2) + x2, at x = 2
Solution:
y = sin (x – 2) + x2
Differentiating w.r.t. x, we get
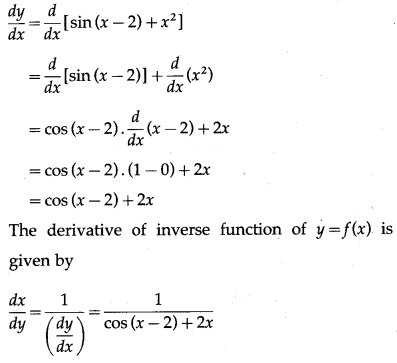
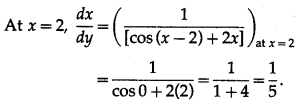
Question 4.
If f(x) = x3 + x – 2, find (f-1)’ (0).
Question is modified.
If f(x) = x3 + x – 2, find (f-1)’ (-2).
Solution:
f(x) = x3 + x – 2 ….(1)
Differentiating w.r.t. x, we get


Question 5.
Using derivative prove
(i) tan-1x + cot-1x = \(\frac{\pi}{2}\)
Solution:
let f(x) = tan-1x + cot-1x
Differentiating w.r.t. x, we get
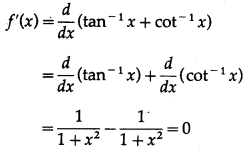
Since, f'(x) = 0, f(x) is a constant function.
Let f(x) = k.
For any value of x, f(x) = k
Let x = 0.
Then f(0) = k ….(2)
From (1), f(0) = tan-1(0) + cot-1(0)
= 0 + \(\frac{\pi}{2}=\frac{\pi}{2}\)
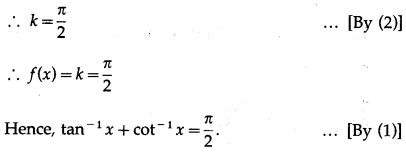
(ii) sec-1x + cosec-1x = \(\frac{\pi}{2}\) . . . [for |x| ≥ 1]
Solution:
Let f(x) = sec-1x + cosec-1x for |x| ≥ 1 ….(1)
Differentiating w.r.t. x, we get
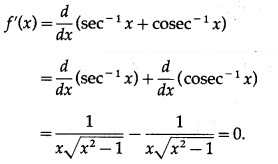
Since, f'(x) = 0, f(x) is a constant function.
Let f(x) = k.
For any value of x, f(x) = k, where |x| > 1
Let x = 2.
Then, f(2) = k ……(2)
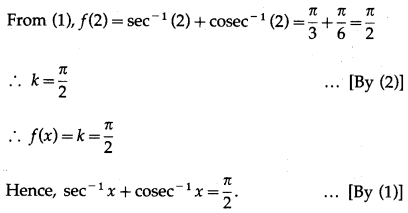

Question 6.
Diffrentiate the following w. r. t. x.
(i) tan-1(log x)
Solution:
Let y = tan-1(log x)
Differentiating w.r.t. x, we get
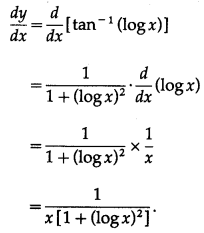
(ii) cosec-1(e-x)
Solution:
Let y = cosec-1(e-x)
Differentiating w.r.t. x, we get
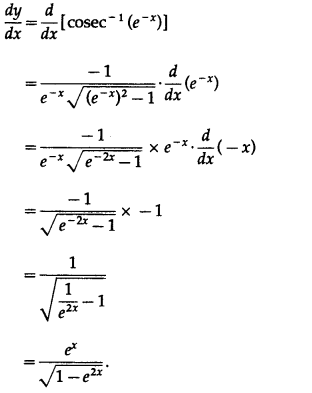
(iii) cot-1(x3)
Solution:
Let y = cot-1(x3)
Differentiating w.r.t. x, we get
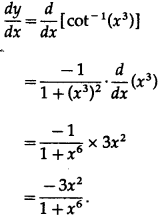

(iv) cot-1(4x
Solution:
Let y = cot-1(4x
Differentiating w.r.t. x, we get
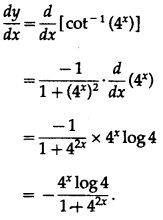
(v) tan-1(\(\sqrt {x}\))
Solution:
Let y = tan-1(\(\sqrt {x}\))
Differentiating w.r.t. x, we get
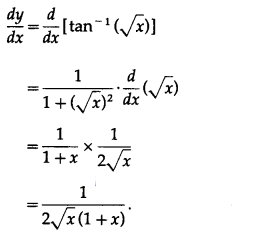
(vi) sin-1\(\left(\sqrt{\frac{1+x^{2}}{2}}\right)\)
Solution:
Let y = sin-1\(\left(\sqrt{\frac{1+x^{2}}{2}}\right)\)
Differentiating w.r.t. x, we get
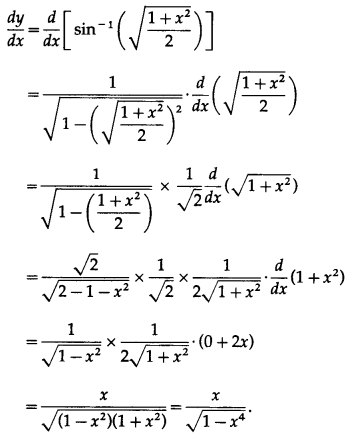

(vii) cos-1(1 – x2)
Solution:
Let y = cos-1(1 – x2)
Differentiating w.r.t. x, we get
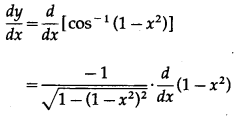
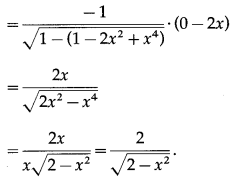
(viii) sin-1\(\left(x^{\frac{3}{2}}\right)\)
Solution:
Let y = sin-1\(\left(x^{\frac{3}{2}}\right)\)
Differentiating w.r.t. x, we get
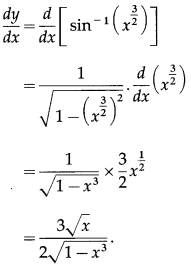

(ix) cos3[cos-1(x3)]
Solution:
Let y = cos3[cos-1(x3)]
= [cos(cos-1x3)]3
= (x3)3 = x9
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(x9) = 9x8.
(x) sin4[sin-1(\(\sqrt {x}\))]
Solution:
Let y = sin4[sin-1(\(\sqrt {x}\))]
= {sin[sin-1(\(\sqrt {x}\))]}8
= (\(\sqrt {x}\))4 = x2
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(x2) = 2x.
Question 7.
Diffrentiate the following w. r. t. x.
(i) cot-1[cot (ex2)]
Solution:
Let y = cot-1[cot (ex2)] = ex2
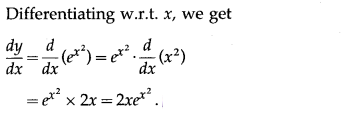

(ii) cosec-1\(\left(\frac{1}{\cos \left(5^{x}\right)}\right)\)
Solution:
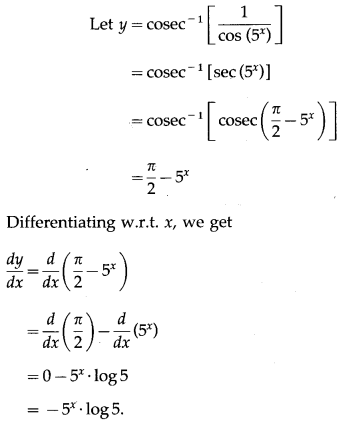
(iii) cos-1\(\left(\sqrt{\frac{1+\cos x}{2}}\right)\)
Solution:

(iv) cos-1\(\left(\sqrt{\frac{1-\cos \left(x^{2}\right)}{2}}\right)\)
Solution:

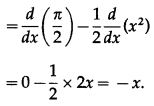
(v) tan-1\(\left(\frac{1-\tan \left(\frac{x}{2}\right)}{1+\tan \left(\frac{x}{2}\right)}\right)\)
Solution:

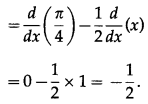

(vi) cosec-1\(\left(\frac{1}{4 \cos ^{3} 2 x-3 \cos 2 x}\right)\)
Solution:

(vii) tan-1\(\left(\frac{1+\cos \left(\frac{x}{3}\right)}{\sin \left(\frac{x}{3}\right)}\right)\)
Solution:
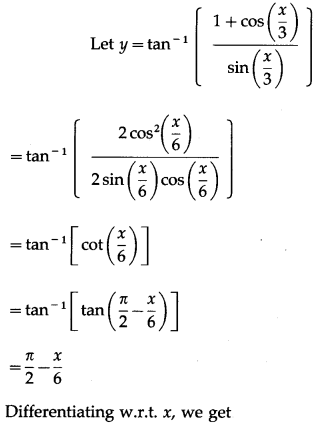
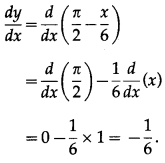
(viii) cot-1\(\left(\frac{\sin 3 x}{1+\cos 3 x}\right)\)
Solution:
Let y = cot-1\(\left(\frac{\sin 3 x}{1+\cos 3 x}\right)\)
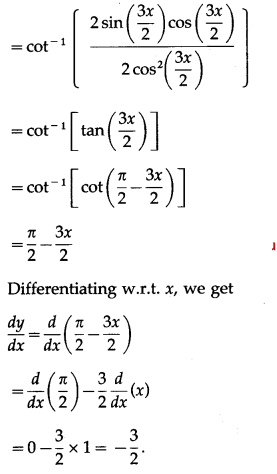

(ix) tan-1\(\left(\frac{\cos 7 x}{1+\sin 7 x}\right)\)
Solution:
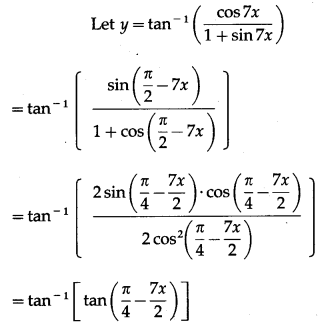
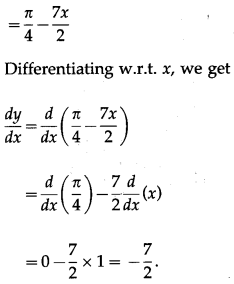
(x) tan-1\(\left(\sqrt{\frac{1+\cos x}{1-\cos x}}\right)\)
Solution:
Let y = tan-1\(\left(\sqrt{\frac{1+\cos x}{1-\cos x}}\right)\)

(xi) tan-1(cosec x + cot x)
Solution:
Let y = tan-1(cosec x + cot x)
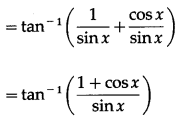
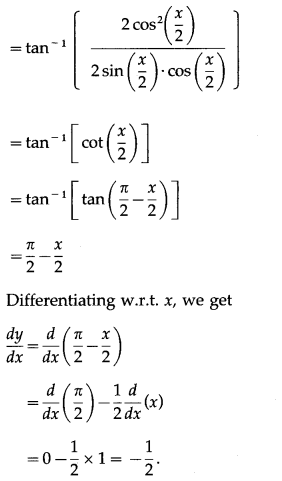

(xii) cot-1\(\left(\frac{\sqrt{1+\sin \left(\frac{4 x}{3}\right)}+\sqrt{1-\sin \left(\frac{4 x}{3}\right)}}{\sqrt{1+\sin \left(\frac{4 x}{3}\right)}-\sqrt{1-\sin \left(\frac{4 x}{3}\right)}}\right)\)
Solution:
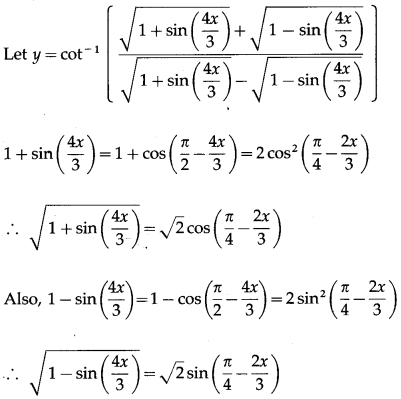
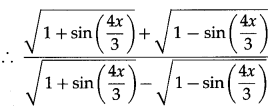
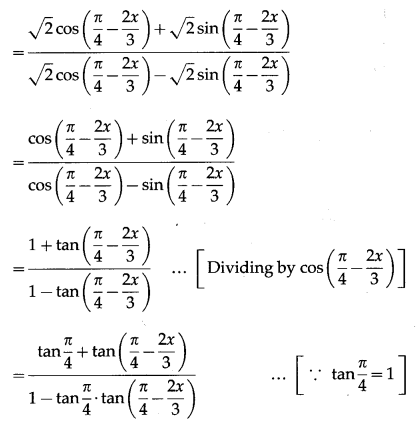
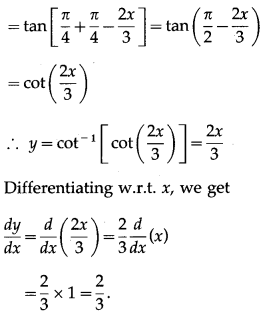
Question 8.
(i)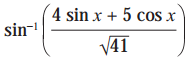
Solution:
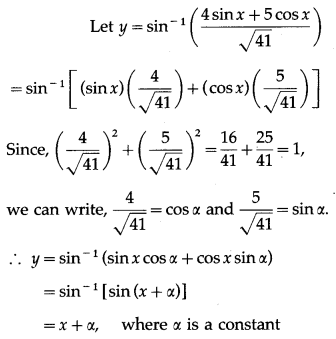
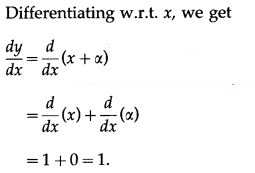
(ii)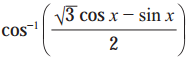
Solution:

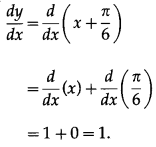

(iii)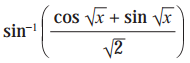
Solution:
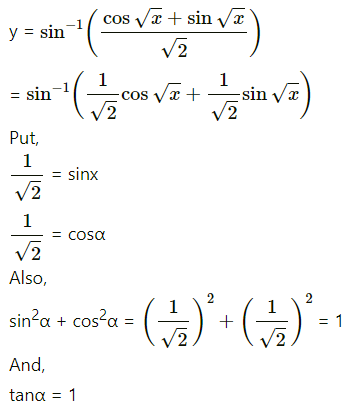
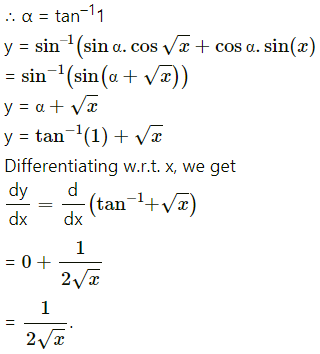
(iv)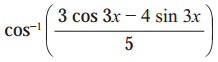
Solution:
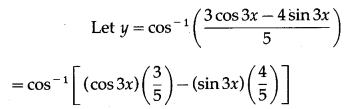
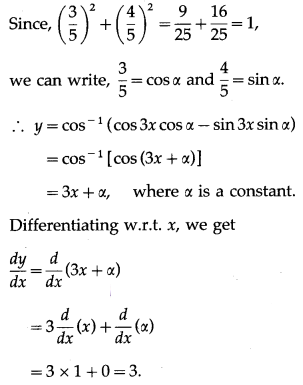
(v)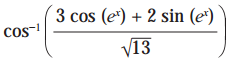
Solution:
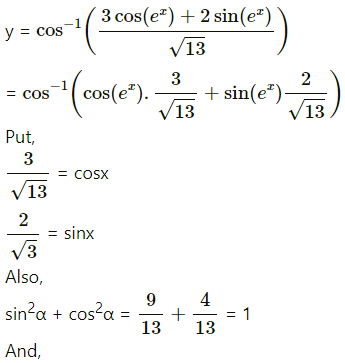
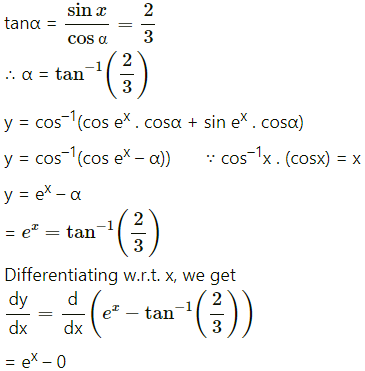
= ex.

(vi)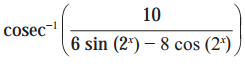
Solution:
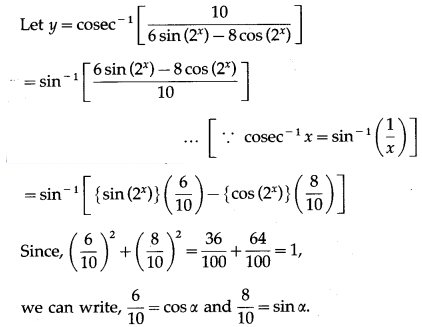
y = sin-1[sin(2x)∙cosα – cos(2x)∙sinα]
= sin–[sin(2x – α)]
= 2x – α, where α is a constant
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(2x – α)
= \(\frac{d}{d x}\)(2x) – \(\frac{d}{d x}\)(α)
= 2x∙log2 – 0
= 2x∙log2
Question 9.
Diffrentiate the following w. r. t. x.
(i) cos-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Solution:
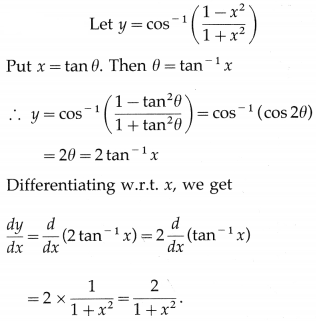
(ii) tan-1\(\left(\frac{2 x}{1-x^{2}}\right)\)
Solution:
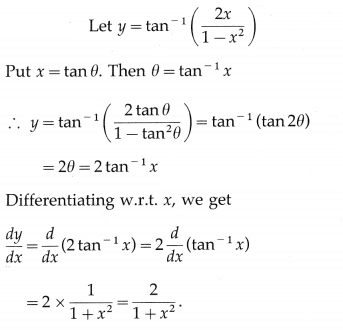

(iii) sin-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Solution:
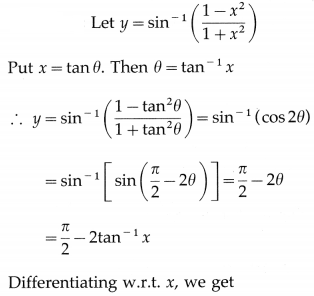
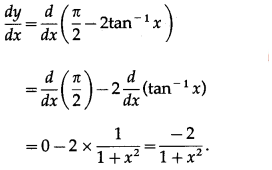
(iv) sin-1(2x\(\sqrt{1-x^{2}}\))
Solution:
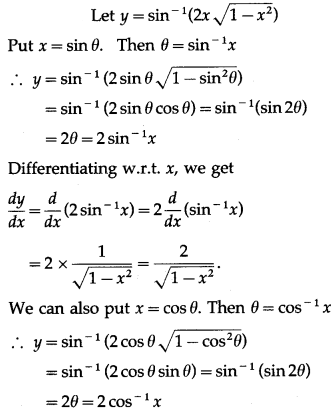
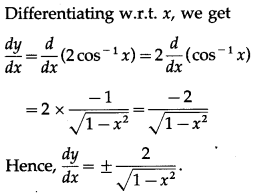
(v) cos-1(3x – 4x3)
Solution:
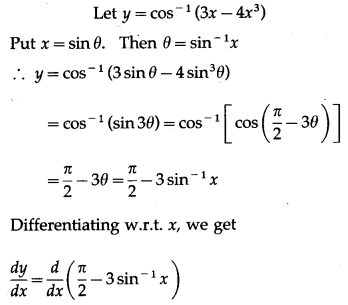
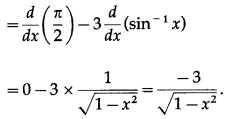
(vi) cos-1\(\left(\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\right)\)
Solution:
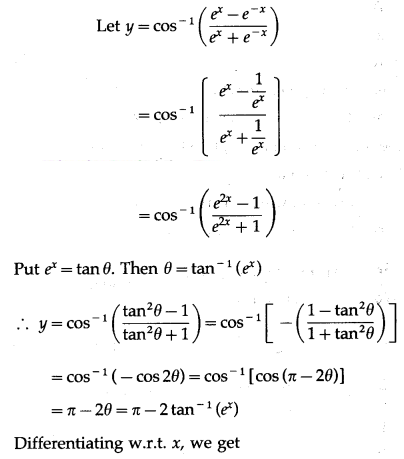
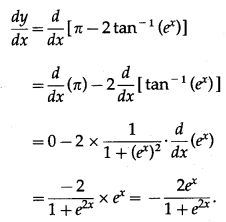

(vii) cos-1\(\left(\frac{1-9^{x}}{1+9^{x}}\right)\)
Solution:
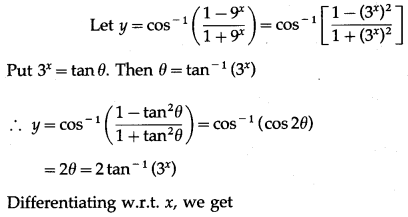
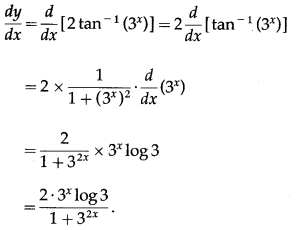
(viii) sin-1\(\left(\frac{4^{x+\frac{1}{2}}}{1+2^{4 x}}\right)\)
Solution:

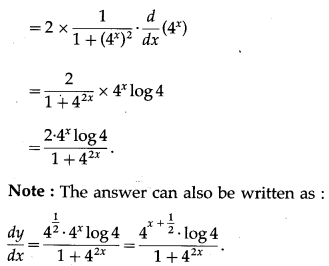
(ix) sin-1\(\left(\frac{1-25 x^{2}}{1+25 x^{2}}\right)\)
Solution:
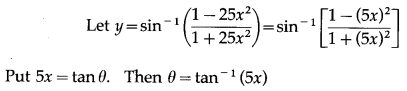
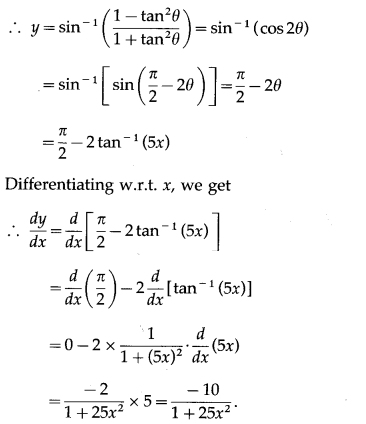
(x) sin-1\(\left(\frac{1-x^{3}}{1+x^{3}}\right)\)
Solution:
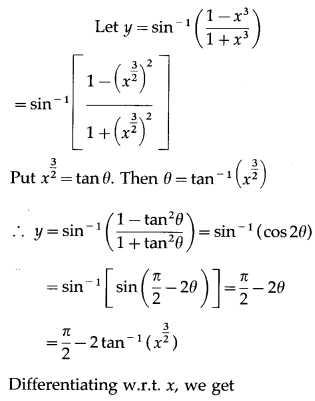
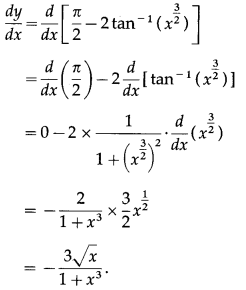

(xi) tan-1\(\left(\frac{2 x^{\frac{5}{2}}}{1-x^{5}}\right)\)

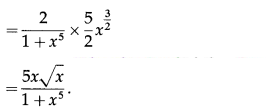
(xii) cot-1\(\left(\frac{1-\sqrt{x}}{1+\sqrt{x}}\right)\)
Solution:
Let y = cot-1\(\left(\frac{1-\sqrt{x}}{1+\sqrt{x}}\right)\)
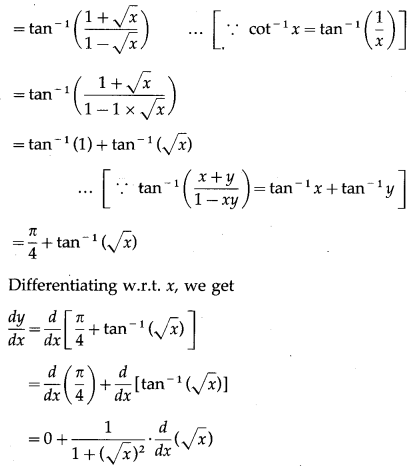
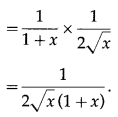
Question 10.
Diffrentiate the following w. r. t. x.
(i) tan-1\(\left(\frac{8 x}{1-15 x^{2}}\right)\)
Solution:
Let y = tan-1\(\left(\frac{8 x}{1-15 x^{2}}\right)\)


(ii) cot-1\(\left(\frac{1+35 x^{2}}{2 x}\right)\)
Solution:
Let y = cot-1\(\left(\frac{1+35 x^{2}}{2 x}\right)\)

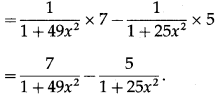
(iii) tan-1\(\left(\frac{2 \sqrt{x}}{1+3 x}\right)\)
Solution:
Let y = tan-1\(\left(\frac{2 \sqrt{x}}{1+3 x}\right)\)
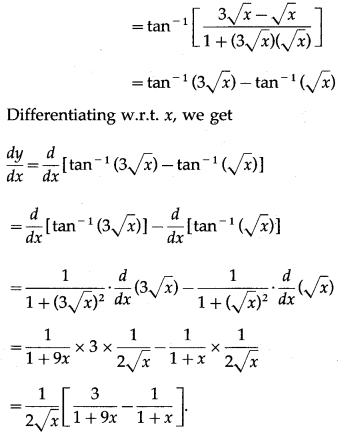
(iv) tan-1\(\left(\frac{2^{x+2}}{1-3\left(4^{x}\right)}\right)\)
Solution:
Let y = tan-1\(\left(\frac{2^{x+2}}{1-3\left(4^{x}\right)}\right)\)
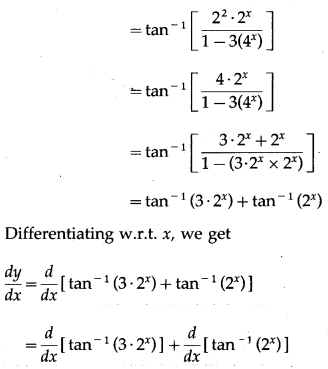
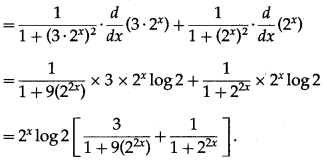

(v) tan-1\(\left(\frac{2^{x}}{1+2^{2 x+1}}\right)\)
Solution:
Let y = tan-1\(\left(\frac{2^{x}}{1+2^{2 x+1}}\right)\)
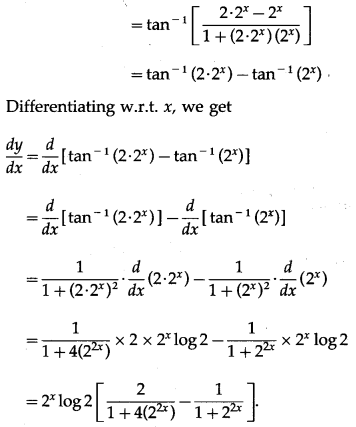
(vi) cot-1\(\left(\frac{a^{2}-6 x^{2}}{5 a x}\right)\)
Solution:
Let y = cot-1\(\left(\frac{a^{2}-6 x^{2}}{5 a x}\right)\)

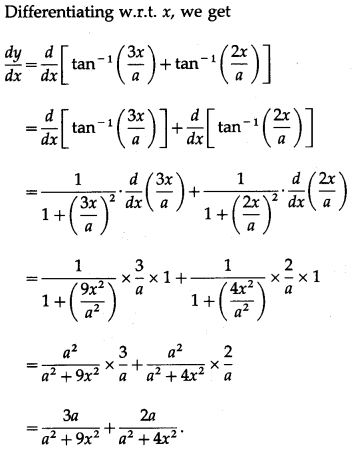
(vii) tan-1\(\left(\frac{a+b \tan x}{b-a \tan x}\right)\)
Solution:
Let y = tan-1\(\left(\frac{a+b \tan x}{b-a \tan x}\right)\)


(viii) tan-1\(\left(\frac{5-x}{6 x^{2}-5 x-3}\right)\)
Solution:
Let y = tan-1\(\left(\frac{5-x}{6 x^{2}-5 x-3}\right)\)
= tan-1\(\left[\frac{5-x}{1+\left(6 x^{2}-5 x-4\right)}\right]\)
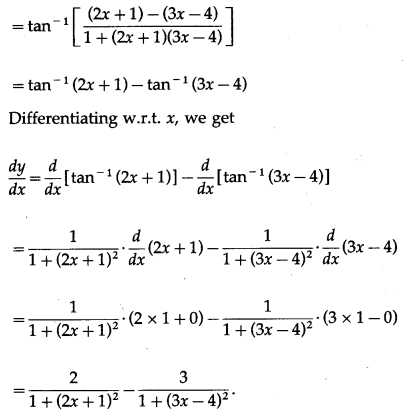
(ix) cot-1\(\left(\frac{4-x-2 x^{2}}{3 x+2}\right)\)
Solution:
Let y = cot-1\(\left(\frac{4-x-2 x^{2}}{3 x+2}\right)\)
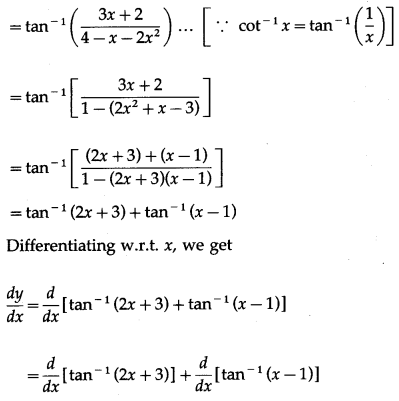
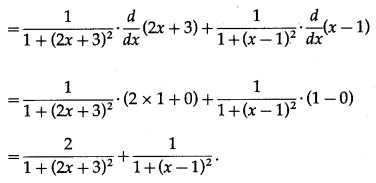
Pdf Chapter 1 Differentiation Ex 1.2 Questions and Answers.
Question 1.
Find the derivative of the function y = f(x) using the derivative of the inverse function x = f-1( y) in the following
(i) y = \(\sqrt {x}\)
Solution:
y = \(\sqrt {x}\) … (1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
y2 = x ∴ x = y2
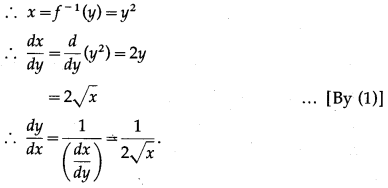
(ii) y = \(\sqrt{2-\sqrt{x}}\)
Solution:
y = \(\sqrt{2-\sqrt{x}}\) …(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
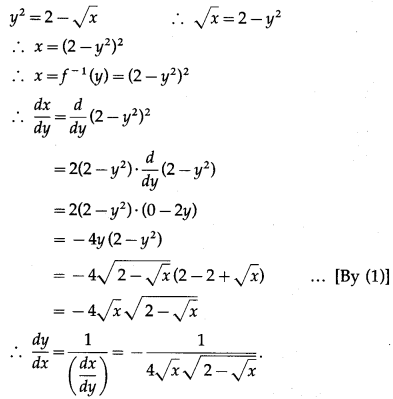
(iii) y = \(\sqrt[3]{x-2}\)
Solution:
y = \(\sqrt[3]{x-2}\) ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
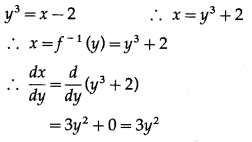
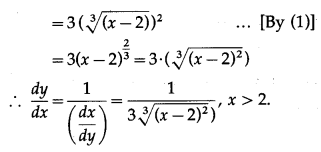

(iv) y = log (2x – 1)
Solution:
y = log (2x – 1) …(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
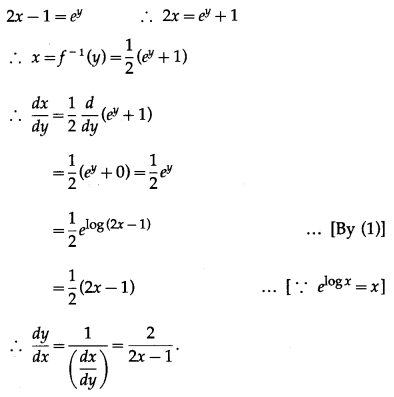
(v) y = 2x + 3
Solution:
y = 2x + 3 ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
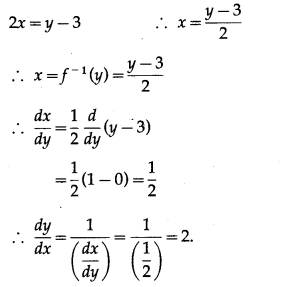
(vi) y = ex – 3
Solution:
y = ex – 3 ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
ex = y + 3
∴ x = log(y + 3)
∴ x = f-1(y) = log(y + 3)
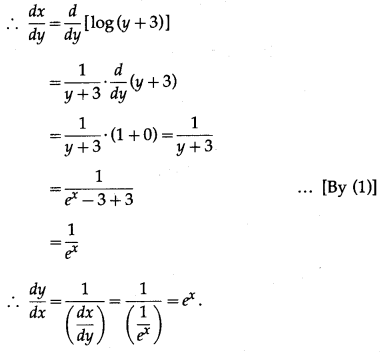

(vii) y = e2x – 3
Solution:
y = e2x – 3 ….(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
2x – 3 = log y ∴ 2x = log y + 3

(viii) y = log2\(\left(\frac{x}{2}\right)\)
Solution:
y = log2\(\left(\frac{x}{2}\right)\) …(1)
We have to find the inverse function of y = f(x), i.e. x in terms of y.
From (1),
\(\frac{x}{2}\) = 2y ∴ x = 2∙2y = 2y+1
∴ x = f-1(y) = 2y+1
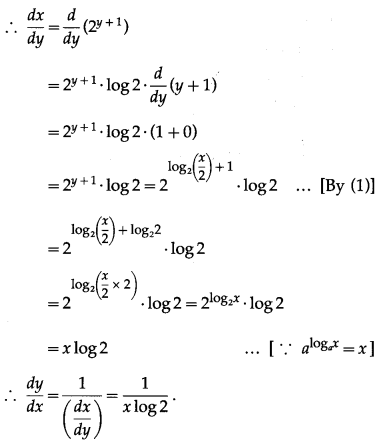
Question 2.
Find the derivative of the inverse function of
the following
(i) y = x2·ex
Solution:
y = x2·ex
Differentiating w.r.t. x, we get


(ii) y = x cos x
Solution:
y = x cos x
Differentiating w.r.t. x, we get
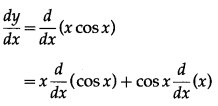
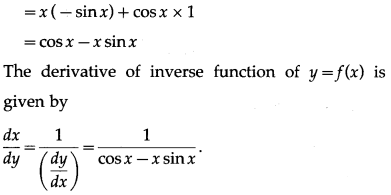
(iii) y = x·7x
Solution:
y = x·7x
Differentiating w.r.t. x, we get

(iv) y = x2 + logx
Solution:
y = x2 + logx
Differentiating w.r.t. x, we get


(v) y = x logx
Solution:
y = x logx
Differentiating w.r.t. x, we get
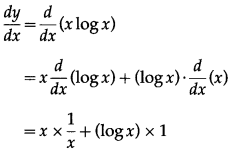

Question 3.
Find the derivative of the inverse of the following functions, and also fid their value at the points indicated against them.
(i) y = x5 + 2x3 + 3x, at x = 1
Solution:
y = x5 + 2x3 + 3x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(x5 + 2x3 + 3x)
= 5x4 + 2 × 3x2 + 3 × 1
= 5x4 + 6x2 + 3
The derivative of inverse function of y = f(x) is given by
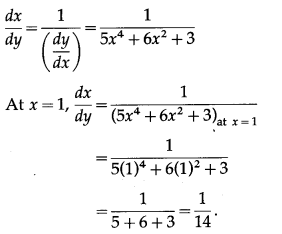
(ii) y = ex + 3x + 2, at x = 0
Solution:
y = ex + 3x + 2
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(ex + 3x + 2)
The derivative of inverse function of y = f(x) is given by
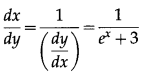
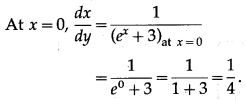

(iii) y = 3x2 + 2 log x3, at x = 1
Solution:
y = 3x2 + 2 log x3
= 3x2 + 6 log x
Differentiating w.r.t. x, we get
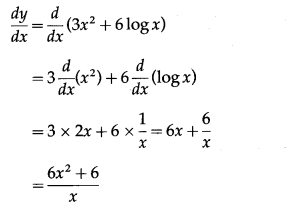
The derivative of inverse function of y = f(x) is given by
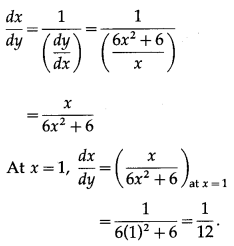
(iv) y = sin (x – 2) + x2, at x = 2
Solution:
y = sin (x – 2) + x2
Differentiating w.r.t. x, we get
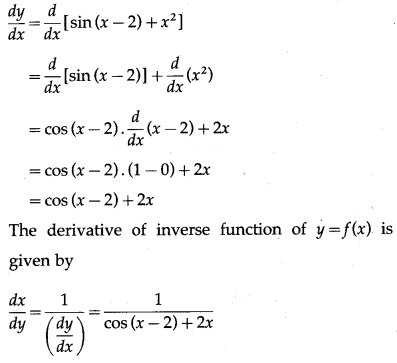
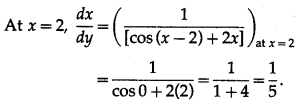
Question 4.
If f(x) = x3 + x – 2, find (f-1)’ (0).
Question is modified.
If f(x) = x3 + x – 2, find (f-1)’ (-2).
Solution:
f(x) = x3 + x – 2 ….(1)
Differentiating w.r.t. x, we get


Question 5.
Using derivative prove
(i) tan-1x + cot-1x = \(\frac{\pi}{2}\)
Solution:
let f(x) = tan-1x + cot-1x
Differentiating w.r.t. x, we get
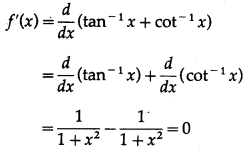
Since, f'(x) = 0, f(x) is a constant function.
Let f(x) = k.
For any value of x, f(x) = k
Let x = 0.
Then f(0) = k ….(2)
From (1), f(0) = tan-1(0) + cot-1(0)
= 0 + \(\frac{\pi}{2}=\frac{\pi}{2}\)
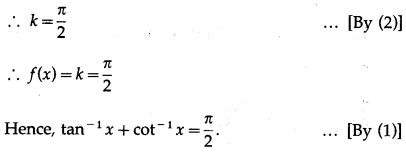
(ii) sec-1x + cosec-1x = \(\frac{\pi}{2}\) . . . [for |x| ≥ 1]
Solution:
Let f(x) = sec-1x + cosec-1x for |x| ≥ 1 ….(1)
Differentiating w.r.t. x, we get
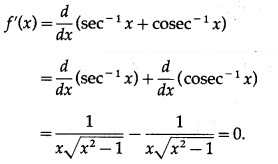
Since, f'(x) = 0, f(x) is a constant function.
Let f(x) = k.
For any value of x, f(x) = k, where |x| > 1
Let x = 2.
Then, f(2) = k ……(2)
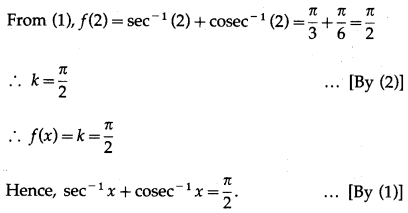

Question 6.
Diffrentiate the following w. r. t. x.
(i) tan-1(log x)
Solution:
Let y = tan-1(log x)
Differentiating w.r.t. x, we get
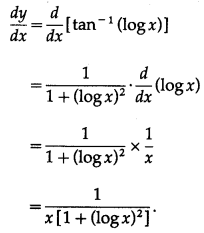
(ii) cosec-1(e-x)
Solution:
Let y = cosec-1(e-x)
Differentiating w.r.t. x, we get
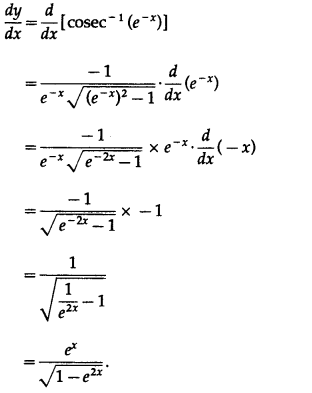
(iii) cot-1(x3)
Solution:
Let y = cot-1(x3)
Differentiating w.r.t. x, we get
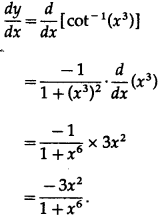

(iv) cot-1(4x
Solution:
Let y = cot-1(4x
Differentiating w.r.t. x, we get
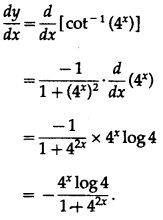
(v) tan-1(\(\sqrt {x}\))
Solution:
Let y = tan-1(\(\sqrt {x}\))
Differentiating w.r.t. x, we get
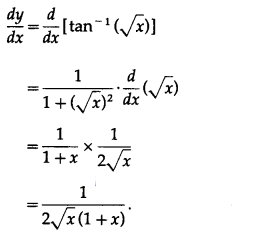
(vi) sin-1\(\left(\sqrt{\frac{1+x^{2}}{2}}\right)\)
Solution:
Let y = sin-1\(\left(\sqrt{\frac{1+x^{2}}{2}}\right)\)
Differentiating w.r.t. x, we get
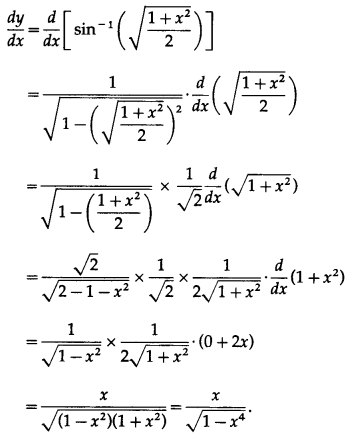

(vii) cos-1(1 – x2)
Solution:
Let y = cos-1(1 – x2)
Differentiating w.r.t. x, we get
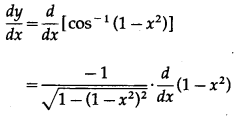
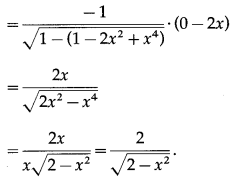
(viii) sin-1\(\left(x^{\frac{3}{2}}\right)\)
Solution:
Let y = sin-1\(\left(x^{\frac{3}{2}}\right)\)
Differentiating w.r.t. x, we get
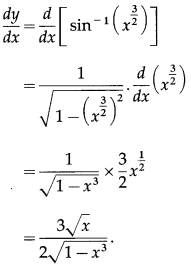

(ix) cos3[cos-1(x3)]
Solution:
Let y = cos3[cos-1(x3)]
= [cos(cos-1x3)]3
= (x3)3 = x9
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(x9) = 9x8.
(x) sin4[sin-1(\(\sqrt {x}\))]
Solution:
Let y = sin4[sin-1(\(\sqrt {x}\))]
= {sin[sin-1(\(\sqrt {x}\))]}8
= (\(\sqrt {x}\))4 = x2
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(x2) = 2x.
Question 7.
Diffrentiate the following w. r. t. x.
(i) cot-1[cot (ex2)]
Solution:
Let y = cot-1[cot (ex2)] = ex2
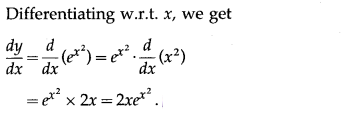

(ii) cosec-1\(\left(\frac{1}{\cos \left(5^{x}\right)}\right)\)
Solution:
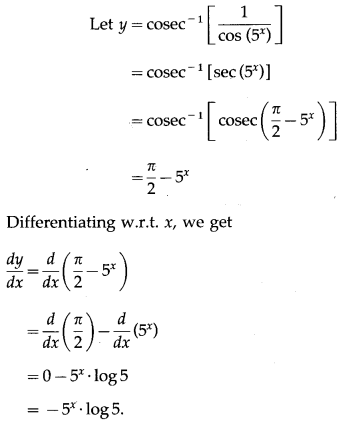
(iii) cos-1\(\left(\sqrt{\frac{1+\cos x}{2}}\right)\)
Solution:

(iv) cos-1\(\left(\sqrt{\frac{1-\cos \left(x^{2}\right)}{2}}\right)\)
Solution:

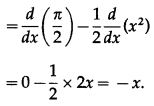
(v) tan-1\(\left(\frac{1-\tan \left(\frac{x}{2}\right)}{1+\tan \left(\frac{x}{2}\right)}\right)\)
Solution:

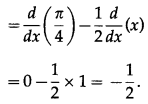

(vi) cosec-1\(\left(\frac{1}{4 \cos ^{3} 2 x-3 \cos 2 x}\right)\)
Solution:

(vii) tan-1\(\left(\frac{1+\cos \left(\frac{x}{3}\right)}{\sin \left(\frac{x}{3}\right)}\right)\)
Solution:
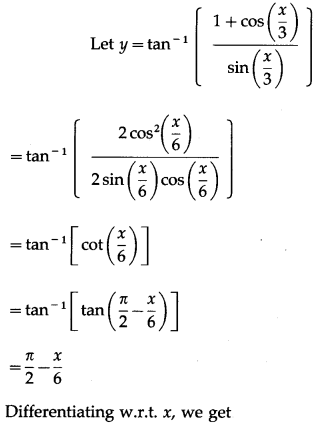
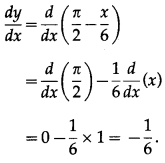
(viii) cot-1\(\left(\frac{\sin 3 x}{1+\cos 3 x}\right)\)
Solution:
Let y = cot-1\(\left(\frac{\sin 3 x}{1+\cos 3 x}\right)\)
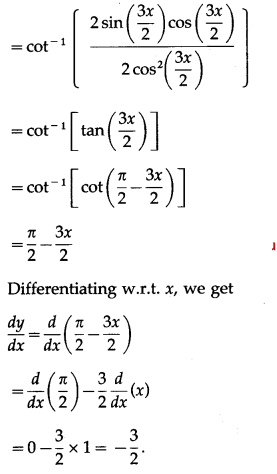

(ix) tan-1\(\left(\frac{\cos 7 x}{1+\sin 7 x}\right)\)
Solution:
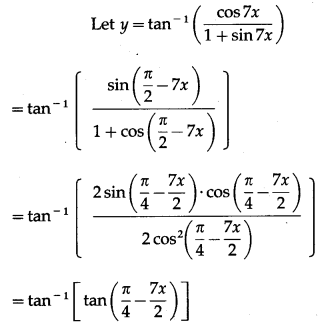
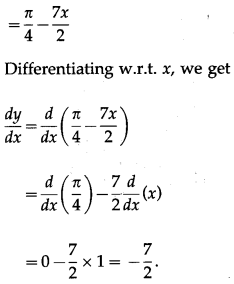
(x) tan-1\(\left(\sqrt{\frac{1+\cos x}{1-\cos x}}\right)\)
Solution:
Let y = tan-1\(\left(\sqrt{\frac{1+\cos x}{1-\cos x}}\right)\)

(xi) tan-1(cosec x + cot x)
Solution:
Let y = tan-1(cosec x + cot x)
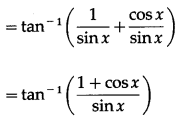
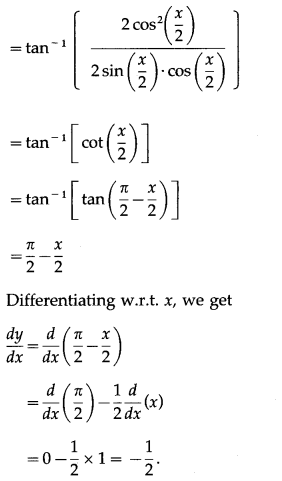

(xii) cot-1\(\left(\frac{\sqrt{1+\sin \left(\frac{4 x}{3}\right)}+\sqrt{1-\sin \left(\frac{4 x}{3}\right)}}{\sqrt{1+\sin \left(\frac{4 x}{3}\right)}-\sqrt{1-\sin \left(\frac{4 x}{3}\right)}}\right)\)
Solution:
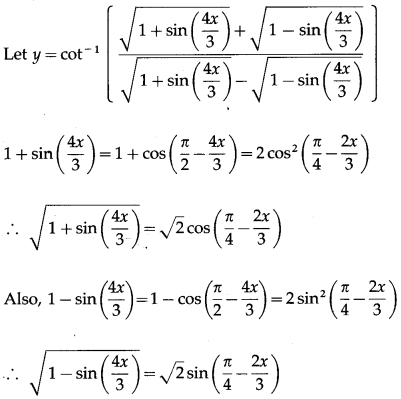
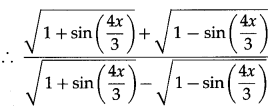
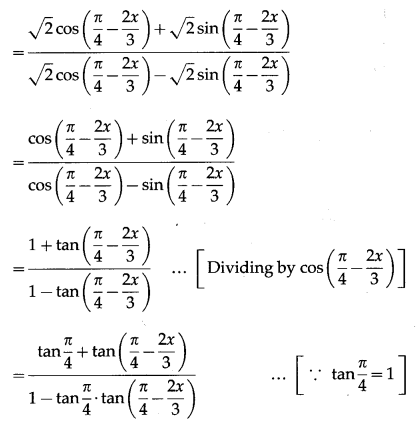
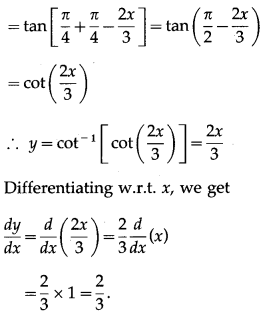
Question 8.
(i)
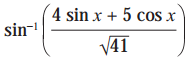
Solution:
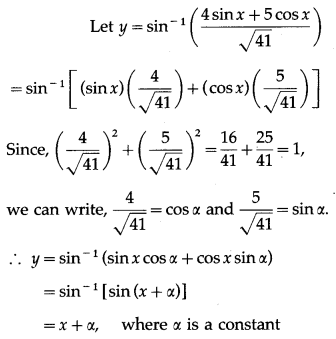
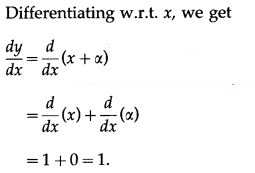
(ii)
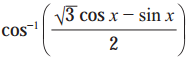
Solution:

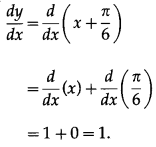

(iii)
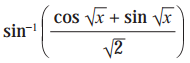
Solution:
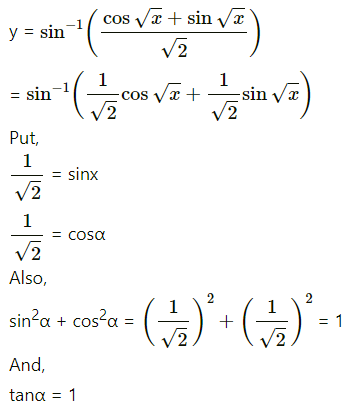
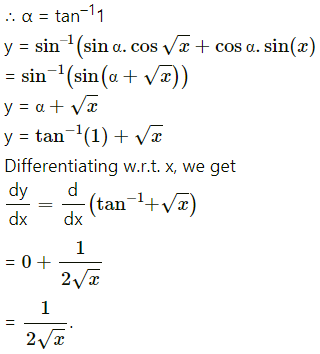
(iv)
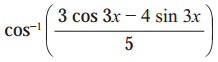
Solution:
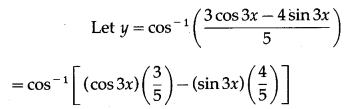
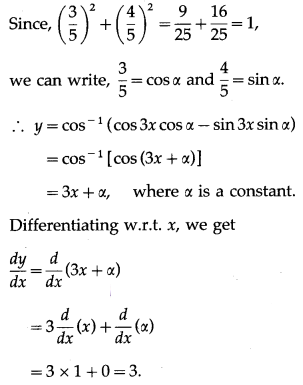
(v)
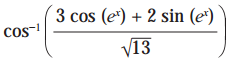
Solution:
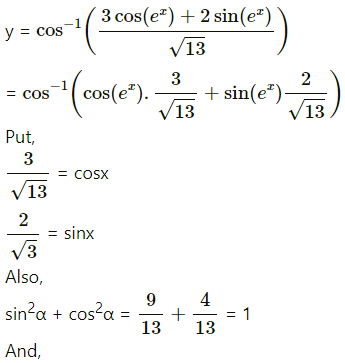
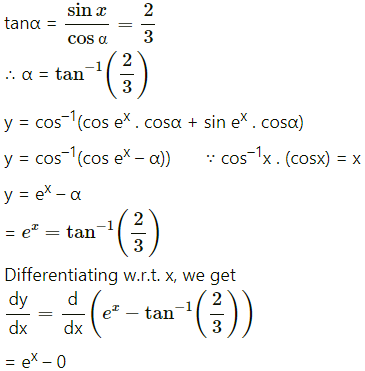
= ex.

(vi)
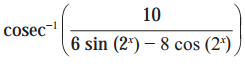
Solution:
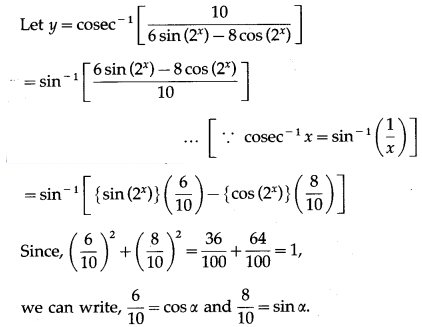
y = sin-1[sin(2x)∙cosα – cos(2x)∙sinα]
= sin–[sin(2x – α)]
= 2x – α, where α is a constant
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\)(2x – α)
= \(\frac{d}{d x}\)(2x) – \(\frac{d}{d x}\)(α)
= 2x∙log2 – 0
= 2x∙log2
Question 9.
Diffrentiate the following w. r. t. x.
(i) cos-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Solution:
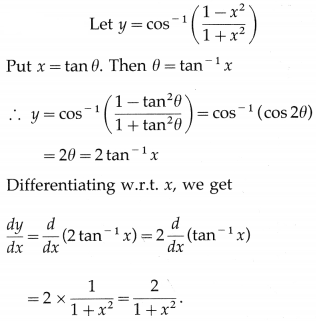
(ii) tan-1\(\left(\frac{2 x}{1-x^{2}}\right)\)
Solution:
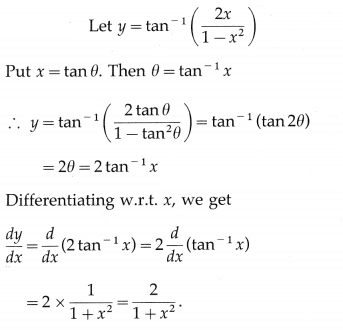

(iii) sin-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
Solution:
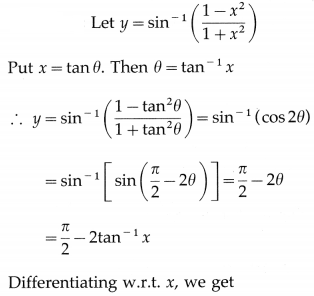
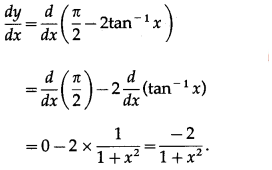
(iv) sin-1(2x\(\sqrt{1-x^{2}}\))
Solution:
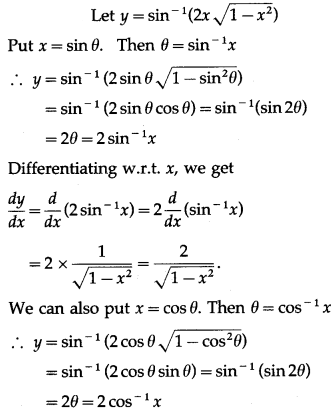
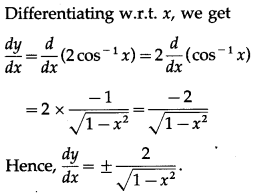
(v) cos-1(3x – 4x3)
Solution:
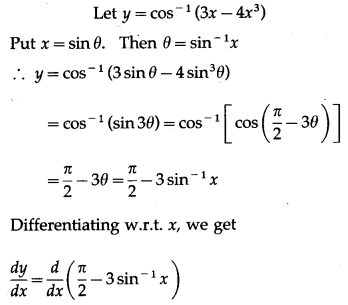
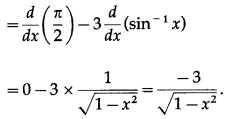
(vi) cos-1\(\left(\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\right)\)
Solution:
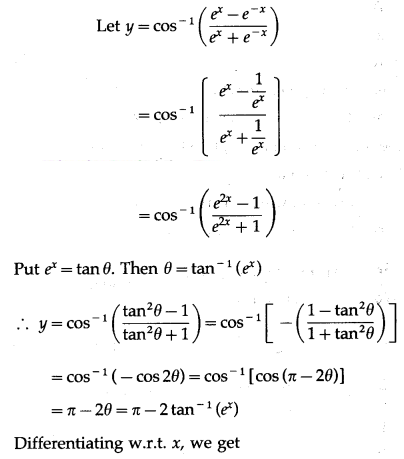
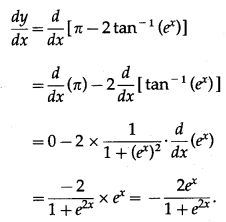

(vii) cos-1\(\left(\frac{1-9^{x}}{1+9^{x}}\right)\)
Solution:
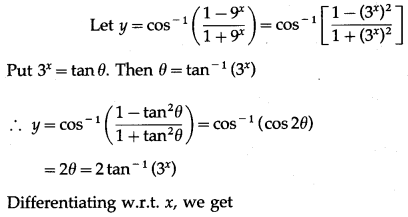
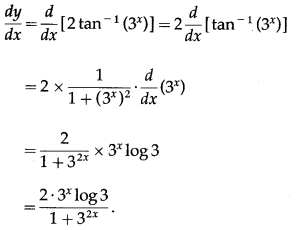
(viii) sin-1\(\left(\frac{4^{x+\frac{1}{2}}}{1+2^{4 x}}\right)\)
Solution:

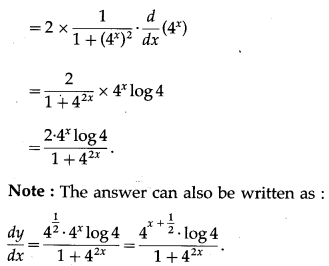
(ix) sin-1\(\left(\frac{1-25 x^{2}}{1+25 x^{2}}\right)\)
Solution:
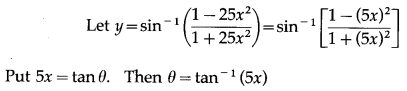
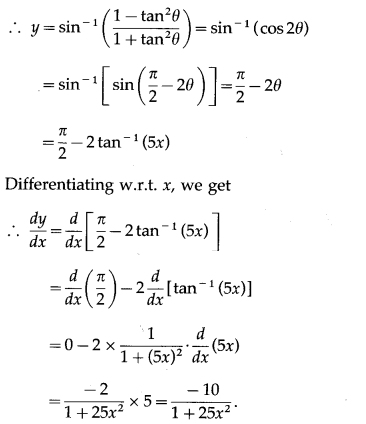
(x) sin-1\(\left(\frac{1-x^{3}}{1+x^{3}}\right)\)
Solution:
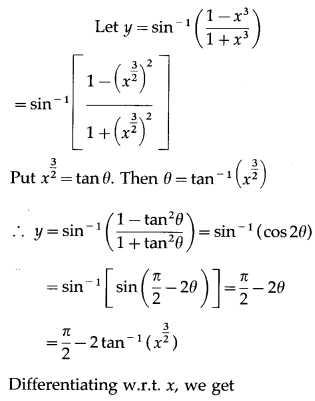
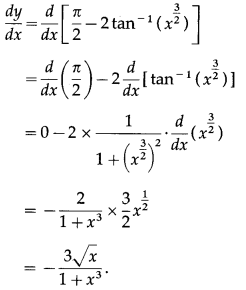

(xi) tan-1\(\left(\frac{2 x^{\frac{5}{2}}}{1-x^{5}}\right)\)

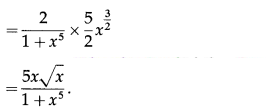
(xii) cot-1\(\left(\frac{1-\sqrt{x}}{1+\sqrt{x}}\right)\)
Solution:
Let y = cot-1\(\left(\frac{1-\sqrt{x}}{1+\sqrt{x}}\right)\)
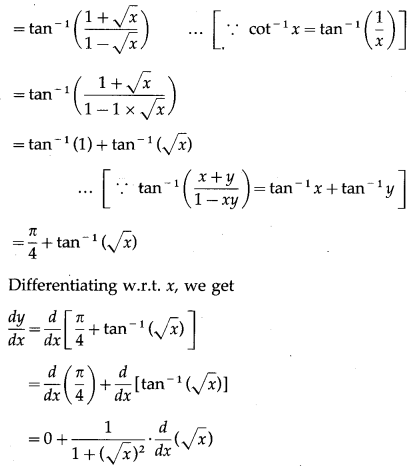
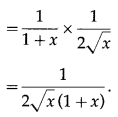
Question 10.
Diffrentiate the following w. r. t. x.
(i) tan-1\(\left(\frac{8 x}{1-15 x^{2}}\right)\)
Solution:
Let y = tan-1\(\left(\frac{8 x}{1-15 x^{2}}\right)\)


(ii) cot-1\(\left(\frac{1+35 x^{2}}{2 x}\right)\)
Solution:
Let y = cot-1\(\left(\frac{1+35 x^{2}}{2 x}\right)\)

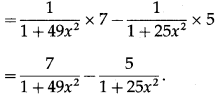
(iii) tan-1\(\left(\frac{2 \sqrt{x}}{1+3 x}\right)\)
Solution:
Let y = tan-1\(\left(\frac{2 \sqrt{x}}{1+3 x}\right)\)
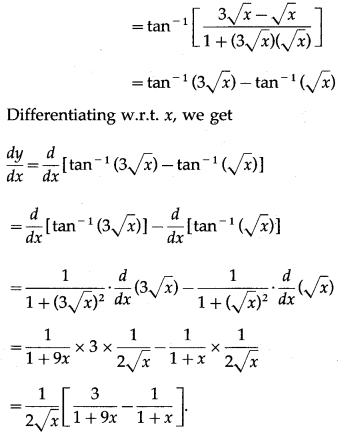
(iv) tan-1\(\left(\frac{2^{x+2}}{1-3\left(4^{x}\right)}\right)\)
Solution:
Let y = tan-1\(\left(\frac{2^{x+2}}{1-3\left(4^{x}\right)}\right)\)
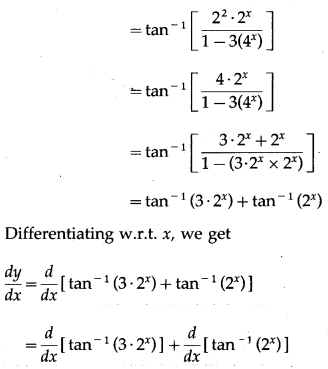
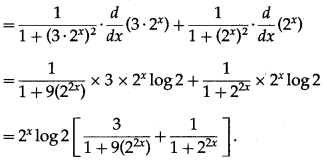

(v) tan-1\(\left(\frac{2^{x}}{1+2^{2 x+1}}\right)\)
Solution:
Let y = tan-1\(\left(\frac{2^{x}}{1+2^{2 x+1}}\right)\)
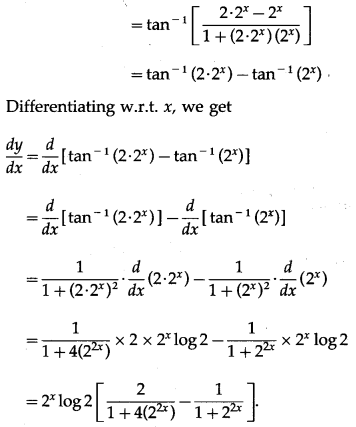
(vi) cot-1\(\left(\frac{a^{2}-6 x^{2}}{5 a x}\right)\)
Solution:
Let y = cot-1\(\left(\frac{a^{2}-6 x^{2}}{5 a x}\right)\)

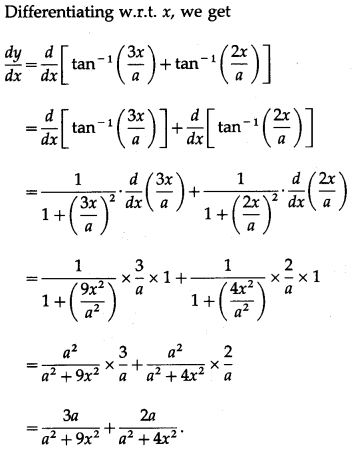
(vii) tan-1\(\left(\frac{a+b \tan x}{b-a \tan x}\right)\)
Solution:
Let y = tan-1\(\left(\frac{a+b \tan x}{b-a \tan x}\right)\)


(viii) tan-1\(\left(\frac{5-x}{6 x^{2}-5 x-3}\right)\)
Solution:
Let y = tan-1\(\left(\frac{5-x}{6 x^{2}-5 x-3}\right)\)
= tan-1\(\left[\frac{5-x}{1+\left(6 x^{2}-5 x-4\right)}\right]\)
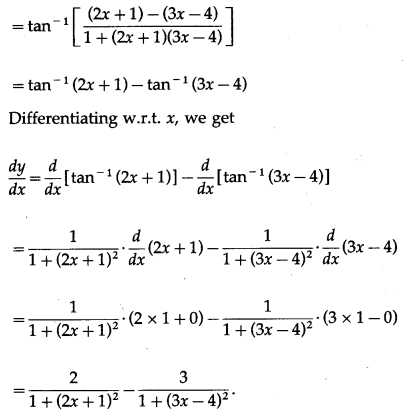
(ix) cot-1\(\left(\frac{4-x-2 x^{2}}{3 x+2}\right)\)
Solution:
Let y = cot-1\(\left(\frac{4-x-2 x^{2}}{3 x+2}\right)\)