Balbharti 12th Maharashtra State Board Maths Solutions Book
Pdf Chapter 4 Pair of Straight Lines Ex 4.1 Questions and Answers.
Question 1.
Find the combined equation of the following pairs of lines:
(i) 2x + y = 0 and 3x – y = 0
Solution:
The combined equation of the lines 2x + y = 0 and 3x – y = 0 is
(2x + y)( 3x – y) = 0
∴ 6x2 – 2xy + 3xy – y2 = 0
∴ 6x2 – xy – y2 = 0.
(ii) x + 2y – 1 = 0 and x – 3y + 2 = 0
Solution:
The combined equation of the lines x + 2y – 1 = 0 and x – 3y + 2 = 0 is
(x + 2y – 1)(x – 3y + 2) = 0
∴ x2 – 3xy + 2x + 2xy – 6y2 + 4y – x + 3y – 2 = 0
∴ x2 – xy – 6y2 + x + 7y – 2 = 0.
(iii) Passing through (2, 3) and parallel to the co-ordinate axes.
Solution:
Equations of the coordinate axes are x = 0 and y = 0.
∴ the equations of the lines passing through (2, 3) and parallel to the coordinate axes are x = 2 and
i.e. x – 2 = 0 and y – 3 = 0.
∴ their combined equation is
(x – 2)(y – 3) = 0.
∴ xy – 3x – 2y + 6 = 0.

(iv) Passing through (2, 3) and perpendicular to lines 3x + 2y – 1 = 0 and x – 3y + 2 = 0
Solution:
Let L1 and L2 be the lines passing through the point (2, 3) and perpendicular to the lines 3x + 2y – 1 = 0 and x – 3y + 2 = 0 respectively.
Slopes of the lines 3x + 2y – 1 = 0 and x – 3y + 2 = 0 are \(\frac{-3}{2}\) and \(\frac{-1}{-3}=\frac{1}{3}\) respectively.
∴ slopes of the lines L1 and L2 are \(\frac{2}{3}\) and -3 respectively.
Since the lines L1 and L2 pass through the point (2, 3), their equations are
y – 3 = \(\frac{2}{3}\)(x – 2) and y – 3 = -3 (x – 2)
∴ 3y – 9 = 2x – 4 and y – 3= -3x + 6
∴ 2x – 3y + 5 = 0 and 3x – y – 9 = 0
∴ their combined equation is
(2x – 3y + 5)(3x + y – 9) = 0
∴ 6x2 + 2xy – 18x – 9xy – 3y2 + 27y + 15x + 5y – 45 = 0
∴ 6x2 – 7xy – 3y2 – 3x + 32y – 45 = 0.
(v) Passsing through (-1, 2),one is parallel to x + 3y – 1 = 0 and the other is perpendicular to 2x – 3y – 1 = 0.
Solution:
Let L1 be the line passing through (-1, 2) and parallel to the line x + 3y – 1 = 0 whose slope is –\(\frac{1}{3}\).
∴ slope of the line L1 is –\(\frac{1}{3}\)
∴ equation of the line L1 is
y – 2 = –\(\frac{1}{3}\)(x + 1)
∴ 3y – 6 = -x – 1
∴ x + 3y – 5 = 0
Let L2 be the line passing through (-1, 2) and perpendicular to the line 2x – 3y – 1 = 0
whose slope is \(\frac{-2}{-3}=\frac{2}{3}\).
∴ slope of the line L2 is –\(\frac{3}{2}\)
∴ equation of the line L2 is
y – 2= –\(\frac{3}{2}\)(x + 1)
∴ 2y – 4 = -3x – 3
∴ 3x + 2y – 1 = 0
Hence, the equations of the required lines are
x + 3y – 5 = 0 and 3x + 2y – 1 = 0
∴ their combined equation is
(x + 3y – 5)(3x + 2y – 1) = 0
∴ 3x2 + 2xy – x + 9xy + 6y2 – 3y – 15x – 10y + 5 = 0
∴ 3x2 + 11xy + 6y2 – 16x – 13y + 5 = 0

Question 2.
Find the separate equations of the lines represented by following equations:
(i) 3y2 + 7xy = 0
Solution:
3y2 + 7xy = 0
∴ y(3y + 7x) = 0
∴ the separate equations of the lines are y = 0 and 7x + 3y = 0.
(ii) 5x2 – 9y2 = 0
Solution:
5x2 – 9y2 = 0
∴ (\(\sqrt {5}\) x)2 – (3y)2 = 0
∴ (\(\sqrt {5}\)x + 3y)(\(\sqrt {5}\)x – 3y) = 0
∴ the separate equations of the lines are
\(\sqrt {5}\)x + 3y = 0 and \(\sqrt {5}\)x – 3y = 0.

(iii) x2 – 4xy = 0
Solution:
x2 – 4xy = 0
∴ x(x – 4y) = 0
∴ the separate equations of the lines are x = 0 and x – 4y = 0
(iv) 3x2 – 10xy – 8y2 = 0
Solution:
3x2 – 10xy – 8y2 = 0
∴ 3x2 – 12xy + 2xy – 8y2 = 0
∴ 3x(x – 4y) + 2y(x – 4y) = 0
∴ (x – 4y)(3x +2y) = 0
∴ the separate equations of the lines are x – 4y = 0 and 3x + 2y = 0.
(v) 3x2 – \(2 \sqrt{3}\) xy – 3y2 = 0
Solution:
3x2 – 2\(\sqrt {3}\)xy – 3y2 = 0
∴ 3x2 – 3\(\sqrt {3}\)xy + \(\sqrt {3}\)xy – 3y2 = 0
∴ 3x(x – \(\sqrt {3}\)y) + \(\sqrt {3}\)y(x – \(\sqrt {3}\)y) = 0
∴ (x – \(\sqrt {3}\)y)(3x + \(\sqrt {3}\)y) = 0
∴ the separate equations of the lines are
∴ x – \(\sqrt {3}\)y = 0 and 3x + \(\sqrt {3}\)y = 0.

(vi) x2 + 2(cosec ∝)xy + y2 = 0
Solution:
x2 + 2 (cosec ∝)xy – y2 = 0
i.e. y2 + 2(cosec∝)xy + x2 = 0
Dividing by x2, we get,

∴ the separate equations of the lines are
(cosec ∝ – cot ∝)x + y = 0 and (cosec ∝ + cot ∝)x + y = 0.
(vii) x2 + 2xy tan ∝ – y2 = 0
Solution:
x2 + 2xy tan ∝ – y2 = 0
Dividind by y2
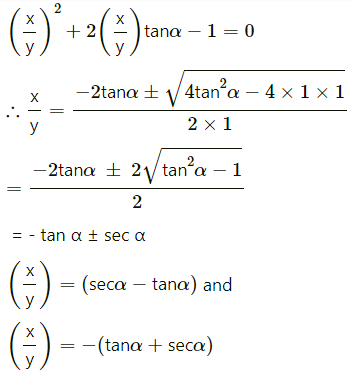
The separate equations of the lines are
(sec∝ – tan ∝)x + y = 0 and (sec ∝ + tan ∝)x – y = 0

Question 3.
Find the combined equation of a pair of lines passing through the origin and perpendicular
to the lines represented by following equations :
(i) 5x2 – 8xy + 3y2 = 0
Solution:
Comparing the equation 5x2 – 8xy + 3y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 5, 2h = -8, b = 3
Let m1 and m2 be the slopes of the lines represented by 5x2 – 8xy + 3y2 = 0.
∴ m1 + m2 = \(\frac{-2 h}{b}=\frac{8}{3}\)
amd m1m2 = \(\frac{a}{b}=\frac{5}{3}\) …(1)
Now required lines are perpendicular to these lines
∴ their slopes are -1 /m1 and -1/m2 Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m1y = -x and m2y = -x
i.e. x + m1y = 0 and x + m2y = 0
∴ their combined equation is
(x + m1y) (x + m2y) = 0
∴ x2 + (m1 + m2)xy + m1m2y2 = 0
∴ x2 + \(\frac{8}{3}\)xy + \(\frac{5}{3}\)y2 = 0 … [By (1)]
∴ x2 + 8xy + 5y\(\frac{8}{3}\) = 0
(ii) 5x2 + 2xy – 3y2 = 0
Solution:
Comparing the equation 5x2 + 2xy – 3y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 5, 2h = 2, b = -3
Let m1 and m2 be the slopes of the lines represented by 5x2 + 2xy – 3y2 = 0
∴ m1 + m2 = \(\frac{-2 h}{b}=\frac{-2}{-3}=\frac{2}{3}\) and m1m2 = \(\frac{a}{b}=\frac{5}{-3}\) ..(1)
Now required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(\frac{-1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{\mathrm{~m}_{1}}\)x and y = \(\frac{-1}{\mathrm{~m}_{2}}\)x
i.e. m1y = -x amd m2y = -x
i.e. x + m1y = 0 and x + m2y = 0
∴ their combined equation is
∴ (x + m1y)(x + m2y) = 0
x2 + (m1 + m2)xy + m1m2y2 = 0
∴ x2 + \(\frac{2}{3}\)xy – \(\frac{5}{3}\)y = 0 …[By (1)]
∴ 3x2 + 2xy – 5y2 = 0

(iii) xy + y2 = 0
Solution:
Comparing the equation xy + y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 0, 2h = 1, b = 1
Let m1 and m2 be the slopes of the lines represented by xy + y2 = 0
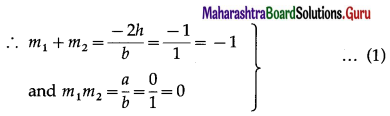
Now required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(\frac{-1}{m_{2}}\).
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m1y = -x and m2y = -x
i.e. x + m1y = 0 and x + m2y = 0
∴ their combined equation is
(x + m1y) (x + m2y) = 0
∴ x2 + (m1 + m2)xy + m1m2y2 = 0
∴ x2 – xy = 0.y2 = 0 … [By (1)]
∴ x2 – xy = 0.
Alternative Method :
Consider xy + y2 = 0
∴ y(x + y) = 0
∴ separate equations of the lines are y = 0 and
3x2 + 8xy + 5y2 = 0.
x + y = 0.
Let m1 and m2 be the slopes of these lines.
Then m1 = 0 and m2 = -1
Now, required lines are perpendicular to these lines.
∴ their slopes are \(-\frac{1}{m_{1}}\) and \(-\frac{1}{m_{2}}\)
Since, m1 = 0, \(-\frac{1}{m_{1}}\) does not exist.
Also, m2 = -1, \(-\frac{1}{m_{2}}\) = 1
Since these lines are passing through the origin, their separate equations are x = 0 and y = x,
i.e. x – y = 0
∴ their combined equation is
x(x – y) = 0
x2 – xy = 0.
(iv) 3x2 – 4xy = 0
Solution:
Consider 3x2 – 4xy = 0
∴ x(3x – 4y) = 0
∴ separate equations of the lines are x = 0 and 3x – 4y = 0.
Let m1 and m2 be the slopes of these lines.
Then m1 does not exist and and m1 = \(\frac{3}{4}\).
Now, required lines are perpendicular to these lines.
∴ their slopes are \(-\frac{1}{m_{1}}\) and \(-\frac{1}{m_{2}}\).
Since m1 does not exist, \(-\frac{1}{m_{1}}\) = 0
Also m2 = \(\frac{3}{4^{\prime}}-\frac{1}{m_{2}}=-\frac{4}{3}\)
Since these lines are passing through the origin, their separate equations are y = 0 and y = \(-\frac{4}{3}\)x,
i.e. 4x + 3y = 0
∴ their combined equation is
y(4x + 3y) = 0
∴ 4xy + 3y2 = 0.

Question 4.
Find k if,
(i) the sum of the slopes of the lines represented by x2 + kxy – 3y2 = 0 is twice their product.
Solution:
Comparing the equation x2 + kxy – 3y2 = 0 with ax2 + 2hxy + by2 = 0, we get, a = 1, 2h = k, b = -3.
Let m1 and m2 be the slopes of the lines represented by x2 + kxy – 3y2 = 0.
∴ m1 + m2 = \(\frac{-2 h}{b}=-\frac{k}{(-3)}=\frac{k}{3}\)
and m1m2 = \(\frac{a}{b}=\frac{1}{(-3)}=-\frac{1}{3}\)
Now, m1 + m2 = 2(m1m2) ..(Given)
∴ \(\frac{k}{3}=2\left(-\frac{1}{3}\right)\) ∴ k = -2
(ii) slopes of lines represent by 3x2 + kxy – y2 = 0 differ by 4.
Solution:
(ii) Comparing the equation 3x2 + kxy – y2 = 0 with ax2 + 2hxy + by2 = 0, we get, a = 3, 2h = k, b = -1.
Let m1 and m2 be the slopes of the lines represented by 3x2 + kxy – y2 = 0.
∴ m1 + m2 = \(\frac{-2 h}{b}=-\frac{k}{-1}\) = k
and m12 = \(\frac{a}{b}=\frac{3}{-1}\) = -3
∴ (m1 – m2)2 = (m1 + m2)2 – 4m1m2
= k2 – 4 (-3)
= k2 + 12 … (1)
But |m1 – m2| =4
∴ (m1 – m2)2 = 16 … (2)
∴ from (1) and (2), k2 + 12 = 16
∴ k2 = 4 ∴ k= ±2.
(iii) slope of one of the lines given by kx2 + 4xy – y2 = 0 exceeds the slope of the other by 8.
Solution:
Comparing the equation kx2 + 4xy – y2 = 0 with 2 + 2hxy + by2 = 0, we get, a = k, 2h = 4, b = -1. Let m1 and m2 be the slopes of the lines represented by kx2 + 4xy – y2 = 0.
∴ m1 + m2 = \(\frac{-2 h}{b}=\frac{-4}{-1}\) = 4
and m1m2 = \(\frac{a}{b}=\frac{k}{-1}\) = -k
We are given that m2 = m1 + 8
m1 + m1 + 8 = 4
∴ 2m1 = -4 ∴ m1 = -2 … (1)
Also, m1(m1 + 8) = -k
(-2)(-2 + 8) = -k … [By(1)]
∴ (-2)(6) = -k
∴ -12= -k ∴ k = 12.

Question 5.
Find the condition that :
(i) the line 4x + 5y = 0 coincides with one of the lines given by ax2 + 2hxy + by2 = 0.
Solution:
The auxiliary equation of the lines represented by ax2 + 2hxy + by2 = 0 is bm2 + 2hm + a = 0.
Given that 4x + 5y = 0 is one of the lines represented by ax2 + 2hxy + by2 = 0.
The slope of the line 4x + 5y = 0 is \(-\frac{4}{5}\).
∴ m = \(-\frac{4}{5}\) is a root of the auxiliary equation bm2 + 2hm + a = 0.
∴ b\(\left(-\frac{4}{5}\right)^{2}\) + 2h\(\left(-\frac{4}{5}\right)\) + a = 0
∴ \(\frac{16 b}{25}-\frac{8 h}{5}\) + a = 0
∴ 16b – 40h + 25a = 0
∴ 25a + 16b = 40k.
This is the required condition.
(ii) the line 3x + y = 0 may be perpendicular to one of the lines given by ax2 + 2hxy + by2 = 0.
Solution:
The auxiliary equation of the lines represented by ax2 + 2hxy + by2 = 0 is bm2 + 2hm + a = 0.
Since one line is perpendicular to the line 3x + y = 0
whose slope is \(-\frac{3}{1}\) = -3
∴ slope of that line = m = \(\frac{1}{3}\)
∴ m = \(\frac{1}{3}\)is the root of the auxiliary equation bm2 + 2hm + a = 0.
∴ b\(\left(\frac{1}{3}\right)^{2}\) + 2h\(\left(\frac{1}{3}\right)\) + a = 0
∴ \(\frac{b}{9}+\frac{2 h}{3}\) + a = 0
∴ b + 6h + 9a = 0
∴ 9a + b + 6h = 0
This is the required condition.

Question 6.
If one of the lines given by ax2 + 2hxy + by2 = 0 is perpendicular to px + qy = 0 then show that ap2 + 2hpq + bq2 = 0.
Solution:
To prove ap2 + 2hpq + bq2 = 0.
Let the slope of the pair of straight lines ax2 + 2hxy + by2 = 0 be m1 and m2
Then, m1 + m2 = \(\frac{-2 h}{b}\) and m1m2 = \(\frac{a}{b}\)
Slope of the line px + qy = 0 is \(\frac{-p}{q}\)
But one of the lines of ax2 + 2hxy + by2 = 0 is perpendicular to px + qy = 0
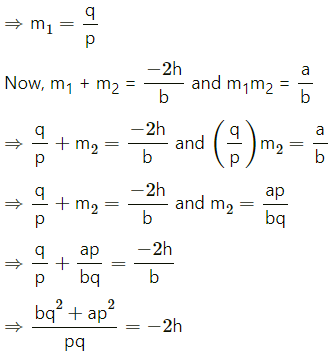
⇒ bq2 + ap2 = -2hpq
⇒ ap2 + 2hpq + bq2 = 0
Question 7.
Find the combined equation of the pair of lines passing through the origin and making an equilateral triangle with the line y = 3.
Solution:
Let OA and OB be the lines through the origin making.an angle of 60° with the line y = 3.
∴ OA and OB make an angle of 60° and 120° with the positive direction of X-axis.
∴ slope of OA = tan60° = \(\sqrt {3}\)
∴ equation of the line OA is
y = \(\sqrt {3}\) x, i.e. \(\sqrt {3}\) x – y = 0
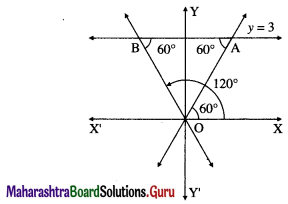
Slope of OB = tan 120° = tan (180° – 60°)
= -tan 60°= –\(\sqrt {3}\)
∴ equation of the line OB is
y = –\(\sqrt {3}\) x, i.e. \(\sqrt {3}\) x + y = 0
∴ required joint equation of the lines is
(\(\sqrt {3}\) x – y)(\(\sqrt {3}\) x + y) = 0
i.e. 3x2 – y2 = 0.
Question 8.
If slope of one of the lines given by ax2 + 2hxy + by2 = 0 is four times the other then show that 16h2 = 25ab.
Solution:
Let m1 and m2 be the slopes of the lines given by ax2 + 2hxy + by2 = 0.
∴ m1 + m2 = \(-\frac{2 h}{b}\)
and m1m2 = \(\frac{a}{b}\)
We are given that m2 = 4m1

∴ 16h2 = 25ab
This is the required condition.
Question 9.
If one of the lines given by ax2 + 2hxy + by2 = 0 bisects an angle between co-ordinate axes then show that (a + b) 2 = 4h2.
Solution:
The auxiliary equation of the lines given by ax2 + 2hxy + by2 = 0 is bm2 + 2hm + a = 0.
Since one of the line bisects an angle between the coordinate axes, that line makes an angle of 45° or 135° with the positive direction of X-axis.
∴ slope of that line = tan45° or tan 135°
∴ m = tan45° = 1
or m = tan 135° = tan (180° – 45°)
= -tan 45°= -1
∴ m = ±1 are the roots of the auxiliary equation bm2 + 2hm + a = 0.
∴ b(±1)2 + 2h(±1) + a = 0
∴ b ± 2h + a = 0
∴ a + b = ±2h
∴ (a + b)2 = 4h2
This is the required condition.
Pdf Chapter 4 Pair of Straight Lines Ex 4.1 Questions and Answers.
Question 1.
Find the combined equation of the following pairs of lines:
(i) 2x + y = 0 and 3x – y = 0
Solution:
The combined equation of the lines 2x + y = 0 and 3x – y = 0 is
(2x + y)( 3x – y) = 0
∴ 6x2 – 2xy + 3xy – y2 = 0
∴ 6x2 – xy – y2 = 0.
(ii) x + 2y – 1 = 0 and x – 3y + 2 = 0
Solution:
The combined equation of the lines x + 2y – 1 = 0 and x – 3y + 2 = 0 is
(x + 2y – 1)(x – 3y + 2) = 0
∴ x2 – 3xy + 2x + 2xy – 6y2 + 4y – x + 3y – 2 = 0
∴ x2 – xy – 6y2 + x + 7y – 2 = 0.
(iii) Passing through (2, 3) and parallel to the co-ordinate axes.
Solution:
Equations of the coordinate axes are x = 0 and y = 0.
∴ the equations of the lines passing through (2, 3) and parallel to the coordinate axes are x = 2 and
i.e. x – 2 = 0 and y – 3 = 0.
∴ their combined equation is
(x – 2)(y – 3) = 0.
∴ xy – 3x – 2y + 6 = 0.

(iv) Passing through (2, 3) and perpendicular to lines 3x + 2y – 1 = 0 and x – 3y + 2 = 0
Solution:
Let L1 and L2 be the lines passing through the point (2, 3) and perpendicular to the lines 3x + 2y – 1 = 0 and x – 3y + 2 = 0 respectively.
Slopes of the lines 3x + 2y – 1 = 0 and x – 3y + 2 = 0 are \(\frac{-3}{2}\) and \(\frac{-1}{-3}=\frac{1}{3}\) respectively.
∴ slopes of the lines L1 and L2 are \(\frac{2}{3}\) and -3 respectively.
Since the lines L1 and L2 pass through the point (2, 3), their equations are
y – 3 = \(\frac{2}{3}\)(x – 2) and y – 3 = -3 (x – 2)
∴ 3y – 9 = 2x – 4 and y – 3= -3x + 6
∴ 2x – 3y + 5 = 0 and 3x – y – 9 = 0
∴ their combined equation is
(2x – 3y + 5)(3x + y – 9) = 0
∴ 6x2 + 2xy – 18x – 9xy – 3y2 + 27y + 15x + 5y – 45 = 0
∴ 6x2 – 7xy – 3y2 – 3x + 32y – 45 = 0.
(v) Passsing through (-1, 2),one is parallel to x + 3y – 1 = 0 and the other is perpendicular to 2x – 3y – 1 = 0.
Solution:
Let L1 be the line passing through (-1, 2) and parallel to the line x + 3y – 1 = 0 whose slope is –\(\frac{1}{3}\).
∴ slope of the line L1 is –\(\frac{1}{3}\)
∴ equation of the line L1 is
y – 2 = –\(\frac{1}{3}\)(x + 1)
∴ 3y – 6 = -x – 1
∴ x + 3y – 5 = 0
Let L2 be the line passing through (-1, 2) and perpendicular to the line 2x – 3y – 1 = 0
whose slope is \(\frac{-2}{-3}=\frac{2}{3}\).
∴ slope of the line L2 is –\(\frac{3}{2}\)
∴ equation of the line L2 is
y – 2= –\(\frac{3}{2}\)(x + 1)
∴ 2y – 4 = -3x – 3
∴ 3x + 2y – 1 = 0
Hence, the equations of the required lines are
x + 3y – 5 = 0 and 3x + 2y – 1 = 0
∴ their combined equation is
(x + 3y – 5)(3x + 2y – 1) = 0
∴ 3x2 + 2xy – x + 9xy + 6y2 – 3y – 15x – 10y + 5 = 0
∴ 3x2 + 11xy + 6y2 – 16x – 13y + 5 = 0

Question 2.
Find the separate equations of the lines represented by following equations:
(i) 3y2 + 7xy = 0
Solution:
3y2 + 7xy = 0
∴ y(3y + 7x) = 0
∴ the separate equations of the lines are y = 0 and 7x + 3y = 0.
(ii) 5x2 – 9y2 = 0
Solution:
5x2 – 9y2 = 0
∴ (\(\sqrt {5}\) x)2 – (3y)2 = 0
∴ (\(\sqrt {5}\)x + 3y)(\(\sqrt {5}\)x – 3y) = 0
∴ the separate equations of the lines are
\(\sqrt {5}\)x + 3y = 0 and \(\sqrt {5}\)x – 3y = 0.

(iii) x2 – 4xy = 0
Solution:
x2 – 4xy = 0
∴ x(x – 4y) = 0
∴ the separate equations of the lines are x = 0 and x – 4y = 0
(iv) 3x2 – 10xy – 8y2 = 0
Solution:
3x2 – 10xy – 8y2 = 0
∴ 3x2 – 12xy + 2xy – 8y2 = 0
∴ 3x(x – 4y) + 2y(x – 4y) = 0
∴ (x – 4y)(3x +2y) = 0
∴ the separate equations of the lines are x – 4y = 0 and 3x + 2y = 0.
(v) 3x2 – \(2 \sqrt{3}\) xy – 3y2 = 0
Solution:
3x2 – 2\(\sqrt {3}\)xy – 3y2 = 0
∴ 3x2 – 3\(\sqrt {3}\)xy + \(\sqrt {3}\)xy – 3y2 = 0
∴ 3x(x – \(\sqrt {3}\)y) + \(\sqrt {3}\)y(x – \(\sqrt {3}\)y) = 0
∴ (x – \(\sqrt {3}\)y)(3x + \(\sqrt {3}\)y) = 0
∴ the separate equations of the lines are
∴ x – \(\sqrt {3}\)y = 0 and 3x + \(\sqrt {3}\)y = 0.

(vi) x2 + 2(cosec ∝)xy + y2 = 0
Solution:
x2 + 2 (cosec ∝)xy – y2 = 0
i.e. y2 + 2(cosec∝)xy + x2 = 0
Dividing by x2, we get,

∴ the separate equations of the lines are
(cosec ∝ – cot ∝)x + y = 0 and (cosec ∝ + cot ∝)x + y = 0.
(vii) x2 + 2xy tan ∝ – y2 = 0
Solution:
x2 + 2xy tan ∝ – y2 = 0
Dividind by y2
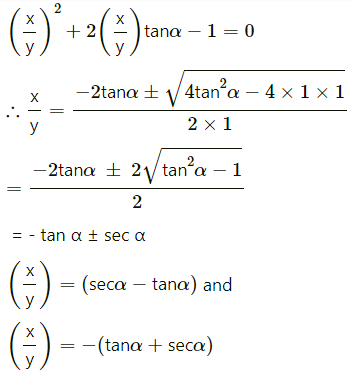
The separate equations of the lines are
(sec∝ – tan ∝)x + y = 0 and (sec ∝ + tan ∝)x – y = 0

Question 3.
Find the combined equation of a pair of lines passing through the origin and perpendicular
to the lines represented by following equations :
(i) 5x2 – 8xy + 3y2 = 0
Solution:
Comparing the equation 5x2 – 8xy + 3y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 5, 2h = -8, b = 3
Let m1 and m2 be the slopes of the lines represented by 5x2 – 8xy + 3y2 = 0.
∴ m1 + m2 = \(\frac{-2 h}{b}=\frac{8}{3}\)
amd m1m2 = \(\frac{a}{b}=\frac{5}{3}\) …(1)
Now required lines are perpendicular to these lines
∴ their slopes are -1 /m1 and -1/m2 Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m1y = -x and m2y = -x
i.e. x + m1y = 0 and x + m2y = 0
∴ their combined equation is
(x + m1y) (x + m2y) = 0
∴ x2 + (m1 + m2)xy + m1m2y2 = 0
∴ x2 + \(\frac{8}{3}\)xy + \(\frac{5}{3}\)y2 = 0 … [By (1)]
∴ x2 + 8xy + 5y\(\frac{8}{3}\) = 0
(ii) 5x2 + 2xy – 3y2 = 0
Solution:
Comparing the equation 5x2 + 2xy – 3y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 5, 2h = 2, b = -3
Let m1 and m2 be the slopes of the lines represented by 5x2 + 2xy – 3y2 = 0
∴ m1 + m2 = \(\frac{-2 h}{b}=\frac{-2}{-3}=\frac{2}{3}\) and m1m2 = \(\frac{a}{b}=\frac{5}{-3}\) ..(1)
Now required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(\frac{-1}{m_{2}}\)
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{\mathrm{~m}_{1}}\)x and y = \(\frac{-1}{\mathrm{~m}_{2}}\)x
i.e. m1y = -x amd m2y = -x
i.e. x + m1y = 0 and x + m2y = 0
∴ their combined equation is
∴ (x + m1y)(x + m2y) = 0
x2 + (m1 + m2)xy + m1m2y2 = 0
∴ x2 + \(\frac{2}{3}\)xy – \(\frac{5}{3}\)y = 0 …[By (1)]
∴ 3x2 + 2xy – 5y2 = 0

(iii) xy + y2 = 0
Solution:
Comparing the equation xy + y2 = 0 with ax2 + 2hxy + by2 = 0, we get,
a = 0, 2h = 1, b = 1
Let m1 and m2 be the slopes of the lines represented by xy + y2 = 0
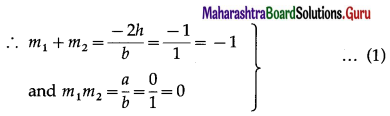
Now required lines are perpendicular to these lines
∴ their slopes are \(\frac{-1}{m_{1}}\) and \(\frac{-1}{m_{2}}\).
Since these lines are passing through the origin, their separate equations are
y = \(\frac{-1}{m_{1}}\)x and y = \(\frac{-1}{m_{2}}\)x
i.e. m1y = -x and m2y = -x
i.e. x + m1y = 0 and x + m2y = 0
∴ their combined equation is
(x + m1y) (x + m2y) = 0
∴ x2 + (m1 + m2)xy + m1m2y2 = 0
∴ x2 – xy = 0.y2 = 0 … [By (1)]
∴ x2 – xy = 0.
Alternative Method :
Consider xy + y2 = 0
∴ y(x + y) = 0
∴ separate equations of the lines are y = 0 and
3x2 + 8xy + 5y2 = 0.
x + y = 0.
Let m1 and m2 be the slopes of these lines.
Then m1 = 0 and m2 = -1
Now, required lines are perpendicular to these lines.
∴ their slopes are \(-\frac{1}{m_{1}}\) and \(-\frac{1}{m_{2}}\)
Since, m1 = 0, \(-\frac{1}{m_{1}}\) does not exist.
Also, m2 = -1, \(-\frac{1}{m_{2}}\) = 1
Since these lines are passing through the origin, their separate equations are x = 0 and y = x,
i.e. x – y = 0
∴ their combined equation is
x(x – y) = 0
x2 – xy = 0.
(iv) 3x2 – 4xy = 0
Solution:
Consider 3x2 – 4xy = 0
∴ x(3x – 4y) = 0
∴ separate equations of the lines are x = 0 and 3x – 4y = 0.
Let m1 and m2 be the slopes of these lines.
Then m1 does not exist and and m1 = \(\frac{3}{4}\).
Now, required lines are perpendicular to these lines.
∴ their slopes are \(-\frac{1}{m_{1}}\) and \(-\frac{1}{m_{2}}\).
Since m1 does not exist, \(-\frac{1}{m_{1}}\) = 0
Also m2 = \(\frac{3}{4^{\prime}}-\frac{1}{m_{2}}=-\frac{4}{3}\)
Since these lines are passing through the origin, their separate equations are y = 0 and y = \(-\frac{4}{3}\)x,
i.e. 4x + 3y = 0
∴ their combined equation is
y(4x + 3y) = 0
∴ 4xy + 3y2 = 0.

Question 4.
Find k if,
(i) the sum of the slopes of the lines represented by x2 + kxy – 3y2 = 0 is twice their product.
Solution:
Comparing the equation x2 + kxy – 3y2 = 0 with ax2 + 2hxy + by2 = 0, we get, a = 1, 2h = k, b = -3.
Let m1 and m2 be the slopes of the lines represented by x2 + kxy – 3y2 = 0.
∴ m1 + m2 = \(\frac{-2 h}{b}=-\frac{k}{(-3)}=\frac{k}{3}\)
and m1m2 = \(\frac{a}{b}=\frac{1}{(-3)}=-\frac{1}{3}\)
Now, m1 + m2 = 2(m1m2) ..(Given)
∴ \(\frac{k}{3}=2\left(-\frac{1}{3}\right)\) ∴ k = -2
(ii) slopes of lines represent by 3x2 + kxy – y2 = 0 differ by 4.
Solution:
(ii) Comparing the equation 3x2 + kxy – y2 = 0 with ax2 + 2hxy + by2 = 0, we get, a = 3, 2h = k, b = -1.
Let m1 and m2 be the slopes of the lines represented by 3x2 + kxy – y2 = 0.
∴ m1 + m2 = \(\frac{-2 h}{b}=-\frac{k}{-1}\) = k
and m12 = \(\frac{a}{b}=\frac{3}{-1}\) = -3
∴ (m1 – m2)2 = (m1 + m2)2 – 4m1m2
= k2 – 4 (-3)
= k2 + 12 … (1)
But |m1 – m2| =4
∴ (m1 – m2)2 = 16 … (2)
∴ from (1) and (2), k2 + 12 = 16
∴ k2 = 4 ∴ k= ±2.
(iii) slope of one of the lines given by kx2 + 4xy – y2 = 0 exceeds the slope of the other by 8.
Solution:
Comparing the equation kx2 + 4xy – y2 = 0 with 2 + 2hxy + by2 = 0, we get, a = k, 2h = 4, b = -1. Let m1 and m2 be the slopes of the lines represented by kx2 + 4xy – y2 = 0.
∴ m1 + m2 = \(\frac{-2 h}{b}=\frac{-4}{-1}\) = 4
and m1m2 = \(\frac{a}{b}=\frac{k}{-1}\) = -k
We are given that m2 = m1 + 8
m1 + m1 + 8 = 4
∴ 2m1 = -4 ∴ m1 = -2 … (1)
Also, m1(m1 + 8) = -k
(-2)(-2 + 8) = -k … [By(1)]
∴ (-2)(6) = -k
∴ -12= -k ∴ k = 12.

Question 5.
Find the condition that :
(i) the line 4x + 5y = 0 coincides with one of the lines given by ax2 + 2hxy + by2 = 0.
Solution:
The auxiliary equation of the lines represented by ax2 + 2hxy + by2 = 0 is bm2 + 2hm + a = 0.
Given that 4x + 5y = 0 is one of the lines represented by ax2 + 2hxy + by2 = 0.
The slope of the line 4x + 5y = 0 is \(-\frac{4}{5}\).
∴ m = \(-\frac{4}{5}\) is a root of the auxiliary equation bm2 + 2hm + a = 0.
∴ b\(\left(-\frac{4}{5}\right)^{2}\) + 2h\(\left(-\frac{4}{5}\right)\) + a = 0
∴ \(\frac{16 b}{25}-\frac{8 h}{5}\) + a = 0
∴ 16b – 40h + 25a = 0
∴ 25a + 16b = 40k.
This is the required condition.
(ii) the line 3x + y = 0 may be perpendicular to one of the lines given by ax2 + 2hxy + by2 = 0.
Solution:
The auxiliary equation of the lines represented by ax2 + 2hxy + by2 = 0 is bm2 + 2hm + a = 0.
Since one line is perpendicular to the line 3x + y = 0
whose slope is \(-\frac{3}{1}\) = -3
∴ slope of that line = m = \(\frac{1}{3}\)
∴ m = \(\frac{1}{3}\)is the root of the auxiliary equation bm2 + 2hm + a = 0.
∴ b\(\left(\frac{1}{3}\right)^{2}\) + 2h\(\left(\frac{1}{3}\right)\) + a = 0
∴ \(\frac{b}{9}+\frac{2 h}{3}\) + a = 0
∴ b + 6h + 9a = 0
∴ 9a + b + 6h = 0
This is the required condition.

Question 6.
If one of the lines given by ax2 + 2hxy + by2 = 0 is perpendicular to px + qy = 0 then show that ap2 + 2hpq + bq2 = 0.
Solution:
To prove ap2 + 2hpq + bq2 = 0.
Let the slope of the pair of straight lines ax2 + 2hxy + by2 = 0 be m1 and m2
Then, m1 + m2 = \(\frac{-2 h}{b}\) and m1m2 = \(\frac{a}{b}\)
Slope of the line px + qy = 0 is \(\frac{-p}{q}\)
But one of the lines of ax2 + 2hxy + by2 = 0 is perpendicular to px + qy = 0
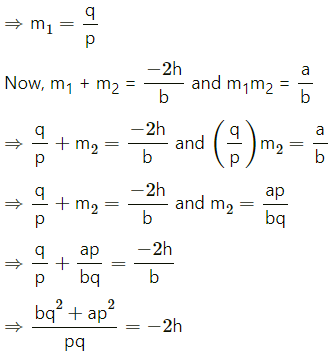
⇒ bq2 + ap2 = -2hpq
⇒ ap2 + 2hpq + bq2 = 0
Question 7.
Find the combined equation of the pair of lines passing through the origin and making an equilateral triangle with the line y = 3.
Solution:
Let OA and OB be the lines through the origin making.an angle of 60° with the line y = 3.
∴ OA and OB make an angle of 60° and 120° with the positive direction of X-axis.
∴ slope of OA = tan60° = \(\sqrt {3}\)
∴ equation of the line OA is
y = \(\sqrt {3}\) x, i.e. \(\sqrt {3}\) x – y = 0

Slope of OB = tan 120° = tan (180° – 60°)
= -tan 60°= –\(\sqrt {3}\)
∴ equation of the line OB is
y = –\(\sqrt {3}\) x, i.e. \(\sqrt {3}\) x + y = 0
∴ required joint equation of the lines is
(\(\sqrt {3}\) x – y)(\(\sqrt {3}\) x + y) = 0
i.e. 3x2 – y2 = 0.
Question 8.
If slope of one of the lines given by ax2 + 2hxy + by2 = 0 is four times the other then show that 16h2 = 25ab.
Solution:
Let m1 and m2 be the slopes of the lines given by ax2 + 2hxy + by2 = 0.
∴ m1 + m2 = \(-\frac{2 h}{b}\)
and m1m2 = \(\frac{a}{b}\)
We are given that m2 = 4m1

∴ 16h2 = 25ab
This is the required condition.
Question 9.
If one of the lines given by ax2 + 2hxy + by2 = 0 bisects an angle between co-ordinate axes then show that (a + b) 2 = 4h2.
Solution:
The auxiliary equation of the lines given by ax2 + 2hxy + by2 = 0 is bm2 + 2hm + a = 0.
Since one of the line bisects an angle between the coordinate axes, that line makes an angle of 45° or 135° with the positive direction of X-axis.
∴ slope of that line = tan45° or tan 135°
∴ m = tan45° = 1
or m = tan 135° = tan (180° – 45°)
= -tan 45°= -1
∴ m = ±1 are the roots of the auxiliary equation bm2 + 2hm + a = 0.
∴ b(±1)2 + 2h(±1) + a = 0
∴ b ± 2h + a = 0
∴ a + b = ±2h
∴ (a + b)2 = 4h2
This is the required condition.