Balbharti Maharashtra State Board 11th Physics Textbook Solutions
Chapter 5 Gravitation Textbook Exercise Questions and Answers.
1. Choose the correct option.
Question 1.
The value of acceleration due to gravity is maximum at
(A) the equator of the Earth .
(B) the centre of the Earth.
(C) the pole of the Earth.
(D) slightly above the surface of the Earth.
Answer:
(C) the pole of the Earth.
Question 2.
The weight of a particle at the centre of the Earth is _________
(A) infinite.
(B) zero.
(C) same as that at other places.
(D) greater than at the poles.
Answer:
(B) zero.

Question 3.
The gravitational potential due to the Earth is minimum at
(A) the centre of the Earth.
(B) the surface of the Earth.
(C) a points inside the Earth but not at its centre.
(D) infinite distance.
Answer:
(A) the centre of the Earth.
Question 4.
The binding energy of a satellite revolving around planet in a circular orbit is 3 × 109 J. Its kinetic energy is _________
(A) 6 × 109 J
(B) -3 × 109 J
(C) -6 × 10+9 J
(D) 3 × 10+9J
Answer:
(D) 3 × 10+9J
2. Answer the following questions.
Question 1.
State Kepler’s law equal of area.
Answer:
The line that joins a planet and the Sun sweeps equal areas in equal intervals of time.
Question 2.
State Kepler’s law of period.
Answer:
The square of the time period of revolution of a planet around the Sun is proportional to the cube of the semimajor axis of the ellipse traced by the planet.
Question 3.
What are the dimensions of the universal gravitational constant?
Answer:
The dimensions of universal gravitational constant are: [L3M-1T-2].
Question 4.
Define binding energy of a satellite.
Answer:
The minimum energy required by a satellite to escape from Earth ‘s gravitational influence is the binding energy of the satellite.
Question 5.
What do you mean by geostationary satellite?
Answer:
Some satellites that revolve around the Earth in equatorial plane have same sense of rotation as that of the Earth. The also have the same period of rotation as that of the Earth i.e.. 24 hours. Due to this, these satellites appear stationary from the Earth’s surface and are known as geostationary satellites.
Question 6.
State Newton’s law of gravitation.
Answer:
Statement:
Every particle of matter attracts every other particle of matter with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Question 7.
Define escape velocity of a satellite.
Answer:
The minimum velocity with which a both’ should he thrown vertically upwards from the surface of the Earth so that it escapes the Earth ‘s gravitational field, is called the escape velocity (ve) of the body.
Question 8.
What is the variation in acceleration due to gravity with altitude?
Answer:
Variation in acceleration due to gravity due to altitude is given by, gh = g\(\left(\frac{R}{R+h}\right)^{2}\)
where,
gh = acceleration due to gravity of an object placed at h altitude
g = acceleration due to gravity on surface of the Earth
R = radius of the Earth
h = attitude height of the object from the surface of the Earth.
Hence, acceleration due to gravity decreases with increase in altitude.
Question 9.
On which factors does the escape speed of a body from the surface of Earth depend?
Answer:
The escape speed depends only on the mass and radius of the planet.
[Note: Escape velocity does not depend upon the mass of the body]
Question 10.
As we go from one planet to another planet, how will the mass and weight of a body change?
Answer:
Question 11.
What is periodic time of a geostationary satellite?
Answer:
The periodic time of a geostationary satellite is same as that of the Earth i.e., one day or 24 hours.
Question 12.
State Newton’s law of gravitation and express it in vector form.
Answer:
Question 13.
What do you mean by gravitational constant? State its SI units.
Answer:

Question 14.
Why is a minimum two stage rocket necessary for launching of a satellite?
Answer:
Question 15.
State the conditions for various possible orbits of a satellite depending upon the horizontal speed of projection
Answer:
The path of the satellite depends upon the value of horizontal speed of projection vh relative to critical velocity vc and escape velocity ve.
Case (I) vh < vc:
The orbit of satellite is an ellipse with point of projection as apogee and Earth at one of the foci. During this elliptical path, if the satellite passes through the Earth’s atmosphere. it experiences a nonconservative force of air resistance. As a result it loses energy and spirals down to the Earth.
Case (II) vh = vc:
The satellite moves in a stable circular orbit around the Earth.
Case (III) vc < vh < ve:
The satellite moves in an elliptical orbit round the Earth with the point of projection as perigee.
Case (IV) vh = ve
The satellite travels along parabolic path and never returns to the point of projection. Its speed will be zero at infinity.
Case (V) vh > ve:
The satellite escapes from gravitational influence of Earth traversing a hyperbolic path.
3. Answer the following questions in detail.
Question 1.
Derive an expression for critical velocity of a satellite.
Answer:
Expression for critical velocity:

Question 2.
State any four applications of a communication satellite.
Answer:
Applications of communication satellite:
Question 3.
Show that acceleration due to gravity at height h above the Earth’s surface is gh = g(\(\frac{R}{R+h}\))2
Answer:
Variation of g due to altitude:
Question 4.
Draw a labelled diagram to show different trajectories of a satellite depending upon the tangential projection speed.
Answer:
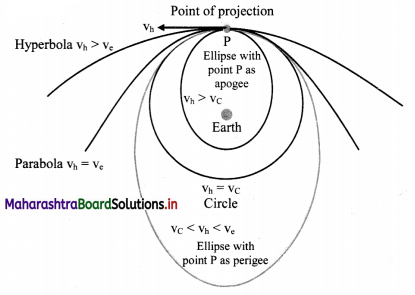
vh = horizontal speed of projection
v c = critical velocity
ve = escape velocity
Question 5.
Derive an expression for binding energy of a body at rest on the Earth’s surface.
Answer:

Question 6.
Why do astronauts in an orbiting satellite have a feeling of weightlessness?
Answer:
Question 7.
Draw a graph showing the variation of gravitational acceleration due to the depth and altitude from the Earth’s surface.
Answer:
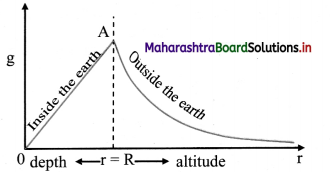
Question 8.
At which place on the Earth’s surface is the gravitational acceleration maximum? Why?
Answer:
Question 9.
At which place on the Earth surface the gravitational acceleration minimum? Why?
Answer:

Question 10.
Define the binding energy of a satellite. Obtain an expression for binding energy of a satellite revolving around the Earth at certain attitude.
Answer:
The minimum energy required by a satellite to escape from Earth ‘s gravitational influence is the binding energy of the satellite.
Expression for binding energy of satellite revolving in circular orbit round the Earth:
Question 11.
Obtain the formula for acceleration due to gravity at the depth ‘d’ below the Earth’s surface.
Answer:
Question 12.
State Kepler’s three laws of planetary motion.
Answer:

Question 13.
State the formula for acceleration due to gravity at depth ‘d’ and altitude ‘h’ Hence show that their ratio is equal to \(\left(\frac{R-d}{R-2 h}\right)\) by assuming that the altitude is very small as compared to the radius of the Earth.
Answer:
Question 14.
What is critical velocity? Obtain an expression for critical velocity of an orbiting satellite. On what factors does it depend?
Answer:
The exact horizontal velocity of projection that must be given to a satellite at a certain height so that it can revolve in a circular orbIt round the Earth is called the critical velocity or orbital velocity (vc).
Expression for critical velocity:
Question 15.
Define escape speed. Derive an expression for the escape speed of an object from the surface of the earth.
Answer:

Question 16.
Describe how an artificial satellite using two stage rocket is launched in an orbit around the Earth.
Answer:
4. Solve the following problems.
Question 1.
At what distance below the surface of the Earth, the acceleration due to gravity decreases by 10% of its value at the surface, given radius of Earth is 6400 km.
Solution:
Given: gd = 90% of g i.e., \(\frac{\mathrm{g}_{\mathrm{d}}}{\mathrm{g}}\) = 0.9,
R = 6400km = 6.4 × 106 m
To find: Distance below the Earth’s surface (d)

At distance 640 km below the surface of the Earth, value of acceleration due to gravity decreases by 10%.
Question 2.
If the Earth were made of wood, the mass of wooden Earth would have been 10% as much as it is now (without change in its diameter). Calculate escape speed from the surface of this Earth.
Solution:

As, we know that the escape speed from surface of the Earth is 11.2 km/s, Substituting value of ve = 11.2 km/s
Vew = 11.2 × \(\frac{1}{\sqrt{10}}=\frac{11.2}{3.162}\)
= 11.2 × \(\frac{1}{3.162}\)
…………… [Taking square root value]
= antilog {log(1 1.2) – Log(3.162)}
= antilog {1.0492 – 0.5000}
= antilog {0.5492} = 3.542
∴ Vew = 3.54km/s
The escape velocity from the surface of wooden Earth is 3.54 km/s.

Question 3.
Calculate the kinetic energy, potential energy, total energy and binding energy of an artificial satellite of mass 2000 kg orbiting at a height of 3600 km above the surface of the Earth.
Given:- G = 6.67 × 10-11 Nm2/kg2
R = 6400 km
M = 6 × 1024 kg
Solution:
Given:- m = 2000 kg, h = 3600 km = 3.6 × 106 m,
G = 6.67 × 10-11 Nm2/kg2
R = 6400 km
M = 6 × 1024 kg
To find: i) Kninetic energy (K.E.)
ii) Potential Energy (P.E.)
iii) Total Energy (T.E.)
iv) Binding Energy (B.E.)

From formula (ii),
P.E. = -2 × 40.02 × 109
= -80.04 × 109 J
From formula (iii),
T.E. = (40.02 × 109) + (-80.02 × 109)
= -40.02 × 109 J
From formula (iv),
B.E.= -(-40.02 × 109)
= 40.02 × 109 J
Kinetic energy of the satellite is 40.02 × 109 J, potential energy is -80.04 × 109 J, total energy is -40.02 × 109 J and binding energy is 40.02 × 109 J.
[Note: Total energy of orbiting satellite is negative.]
Question 4.
Two satellites A and B are revolving around a planet. Their periods of revolution are 1 hour and 8 hours respectively. The radius of orbit of satellite B is 4 × 104 km. find radius of orbit of satellite A .
Solution:
Given: TA = 1 hour, TB = 8 hour,
rB = 4 × 104 km
To find: Radius of orbit of satellite A (rA)

Radius of orbit of satellite A will be 1 × 104 km.
Question 5.
Find the gravitational force between the Sun and the Earth.
Given Mass of the Sun = 1.99 × 1030 kg
Mass of the Earth = 5.98 × 1024 kg
The average distance between the Earth and the Sun = 1.5 × 1011 m.
Solution:
Given: MS = 1.99 × 1030 kg
ME = 5.98 × 1024 kg, R = 1.5 × 1011 m.
To find: Gravitational force between the Sun and the Earth (F)
Formula: F = \(\frac{\mathrm{Gm}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\)
Calculation:As, we know, G = 6.67 × 10-11 N m2/kg2
From formula,

= antilog {(log(6.67) + log( 1.99) + log(5.98) – log(2.25)} × 1021
= antilog {(0.8241) + (0.2989) + (0.7767) – (0.3522)} × 1021
= antilog {1.5475} × 1021
= 35.28 × 1021
= 3.5 × 1022 N
The gravitational force between the Sun and the Earth is 3.5 × 1022 N.

Question 6.
Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 × 1024 kg, R = 6400 km).
Solution:
Given: h = 300 km = 0.3 × 106 m,
M = 5.98 × 1024 kg,
R = 6400km = 6.4 × 106 m
G = 6.67 × 10-11 Nm2/kg2
To find: Acceleration due to gravity at height (gh)
Formula: gh = \(\frac{G M}{(R+h)^{2}}\)
Calculation: From formula,
gh = \(\frac{6.67 \times 10^{-11} \times 5.98 \times 10^{24}}{\left[\left(6.4 \times 10^{6}\right)+\left(0.3 \times 10^{6}\right)\right]^{2}}\)
= \(\frac{6.67 \times 5.98 \times 10^{13}}{(6.7)^{2} \times 10^{12}}\)
6.67 X 10” x 5.98 X iO
= antilog {log(6.67) + log(5.98) – 2log(6.7)} × 10
= antilog{0.8241 + 0.7767 – 2(0.8261)} × 10
= antilog {1.6008 – 1.6522} × 10
= antilog {\(\overline{1}\) .9486} × 10
= 0.8884 × 10 = 8.884 m/s2
Acceleration due to gravity at 300 km will be 8.884 m/s2.
Question 7.
Calculate the speed of a satellite in an orbit at a height of 1000 km from the Earth’s surface. ME = 5.98 × 1024 kg, R = 6.4 × 106 m.
Solution:
Given: h = 1000 km = 1 × 106 m,
ME = 5.98 × 1024 kg, R = 6.4 × 106 m,
G = 6.67 × 10-11 N m2/kg2
To find: Speed of satellite (vc)

Speed of the satellite at height 1000 km is 7.34 × 103 m/s.
Question 8.
Calculate the value of acceleration due to gravity on the surface of Mars if the radius of Mars = 3.4 × 103 km and its mass is 6.4 × 1023 kg.
Solution:
Given:
M = 6.4 × 1023 kg
R = 3.4 × 103 = 3.4 × 106 m,
To find: Acceleration due to gravity on the surface of the Mars (gM)
Formula: g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: As, G = 6.67 × 10-11 N m2/kg2
From formula,
gM = \(\frac{6.67 \times 10^{-11} \times 6.4 \times 10^{23}}{\left(3.4 \times 10^{6}\right)^{2}}=\frac{6.67 \times 6.4}{3.4 \times 3.4}\)
= antilog {log(6.67) + log(6.4) – log(3.4) – log(3.4)}
= antilog {(0.8241) + (0.8062) – (0.5315) – (0.53 15)}
= antilog {0.5673}
= 3.693 m/s2
Acceleration due to gravity on the surface of Mars is 3.693 m/s2.
Question 9.
A planet has mass 6.4 × 1024 kg and radius 3.4 × 106 m. Calculate energy required to remove on object of mass 800 kg from the surface of the planet to infinity.
Solution:
Given: M = 6.4 × 1024 kg, R = 3.4 × 106 m, m = 800 kg
To find: Energy required to remove the object from surface of planet to infinity = B.E.
Formula: B.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\)
Calculation: We know that,
G = 6.67 × 10-11 N m2/kg2
From formula,
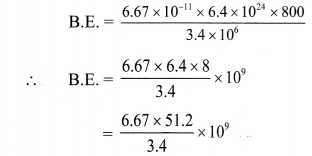
= antilog{log(6.67) + log(51.2) – log(3.4)} × 109
= antilog{0.8241 + 1.7093 – 0.5315} × 109
= antilog {2.0019} × 109
= 1.004 × 102 × 109
= 1.004 × 1011 J
Energy required to remove the object from the surface of the planet is 1.004 × 1011 J.
[Note: Answer calculated above ¡s in accordance with retual methods of calculation.]

Question 10.
Calculate the value of the universal gravitational constant from the given data. Mass of the Earth = 6 × 1024 kg, Radius of the Earth = 6400 km and the acceleration due to gravity on the surface = 9.8 m/s2
Solution:
Given: M = 6 × 1024 kg,
R = 6400km = 6.4 × 106 m,
g = 9.8 m/s2
To find: Gravitational constant (G)
Formula. g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: From formula,
G = \(\frac{\mathrm{gR}^{2}}{\mathrm{M}}\)
G = \(\frac{9.8 \times\left(6.4 \times 10^{6}\right)^{2}}{6 \times 10^{24}}=\frac{401.4 \times 10^{12}}{6 \times 10^{24}}\)
∴ G = 6.69 × 10-11 N m2/kg2
The value of gravitational constant is 6.69 × 10-11 N m2/kg2.
Question 11.
A body weighs 5.6 kg wt on the surface of the Earth. How much will be its weight on a planet whose mass is 1/7 times the mass of the Earth and radius twice that of the Earth’s radius.
Solution:
Given: WE = 5.6 kg-wt.,
\(\frac{\mathrm{M}_{\mathrm{p}}}{\mathrm{M}_{\mathrm{E}}}=\frac{1}{7}, \frac{\mathrm{R}_{\mathrm{p}}}{\mathrm{R}_{\mathrm{E}}}\) = 2
To find: Weight of the body on the surface of planet (Wp)
Formula: W = mg = \(\frac{\mathrm{GMm}}{\mathrm{R}^{2}}\)
Calculation: From formula,
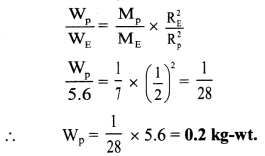
Weight of the body on the surface of a planet will be 0.2 kg-wt.
[Note: The answer given above is calculated in accordance with textual method considering the given data].
Question 12.
What is the gravitational potential due to the Earth at a point which is at a height of 2RE above the surface of the Earth, Mass of the Earth is 6 × 1024 kg, radius of the Earth = 6400 km and G = 6.67 × 10-11 Nm2 kg-2.
Solution:
Given: M = 6 × 1024 kg,
RE = 6400km = 6.4 × 106 m,
G = 6.67 × 10-11 Nm2/kg2,
h = 2RE
To find: Gravitational potential (V)
Formula: V = – \(\frac{\mathrm{GM}}{\mathrm{r}}\)
Calculation: From formula,
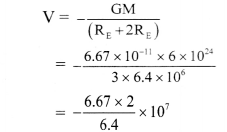
= -2.08 × 107 J kg-1
Negative sign indicates the attractive nature of gravitational potential.
Gravitational potential due to Earth will be 2.08 × 107 J kg-1 towards the centre of the Earth.
[Note: According lo definition of gravitational potential its SI unit is J/kg.]
11th Physics Digest Chapter 5 Gravitation Intext Questions and Answers
Can you recall? (Textbook Page No. 78)
Question 1.
i) What are Kepler’s laws?
ii)What is the shape of the orbits of planets?
Answer:

Question 2.
When released from certain height why do objects tend to fall vertically downwards?
Answer:
When released from certain height, objects tend to fall vertically downwards because of the gravitational force exerted by the Earth.
Chapter 5 Gravitation Textbook Exercise Questions and Answers.
1. Choose the correct option.
Question 1.
The value of acceleration due to gravity is maximum at
(A) the equator of the Earth .
(B) the centre of the Earth.
(C) the pole of the Earth.
(D) slightly above the surface of the Earth.
Answer:
(C) the pole of the Earth.
Question 2.
The weight of a particle at the centre of the Earth is _________
(A) infinite.
(B) zero.
(C) same as that at other places.
(D) greater than at the poles.
Answer:
(B) zero.

Question 3.
The gravitational potential due to the Earth is minimum at
(A) the centre of the Earth.
(B) the surface of the Earth.
(C) a points inside the Earth but not at its centre.
(D) infinite distance.
Answer:
(A) the centre of the Earth.
Question 4.
The binding energy of a satellite revolving around planet in a circular orbit is 3 × 109 J. Its kinetic energy is _________
(A) 6 × 109 J
(B) -3 × 109 J
(C) -6 × 10+9 J
(D) 3 × 10+9J
Answer:
(D) 3 × 10+9J
2. Answer the following questions.
Question 1.
State Kepler’s law equal of area.
Answer:
The line that joins a planet and the Sun sweeps equal areas in equal intervals of time.
Question 2.
State Kepler’s law of period.
Answer:
The square of the time period of revolution of a planet around the Sun is proportional to the cube of the semimajor axis of the ellipse traced by the planet.
Question 3.
What are the dimensions of the universal gravitational constant?
Answer:
The dimensions of universal gravitational constant are: [L3M-1T-2].
Question 4.
Define binding energy of a satellite.
Answer:
The minimum energy required by a satellite to escape from Earth ‘s gravitational influence is the binding energy of the satellite.
Question 5.
What do you mean by geostationary satellite?
Answer:
Some satellites that revolve around the Earth in equatorial plane have same sense of rotation as that of the Earth. The also have the same period of rotation as that of the Earth i.e.. 24 hours. Due to this, these satellites appear stationary from the Earth’s surface and are known as geostationary satellites.
Question 6.
State Newton’s law of gravitation.
Answer:
Statement:
Every particle of matter attracts every other particle of matter with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Question 7.
Define escape velocity of a satellite.
Answer:
The minimum velocity with which a both’ should he thrown vertically upwards from the surface of the Earth so that it escapes the Earth ‘s gravitational field, is called the escape velocity (ve) of the body.
Question 8.
What is the variation in acceleration due to gravity with altitude?
Answer:
Variation in acceleration due to gravity due to altitude is given by, gh = g\(\left(\frac{R}{R+h}\right)^{2}\)
where,
gh = acceleration due to gravity of an object placed at h altitude
g = acceleration due to gravity on surface of the Earth
R = radius of the Earth
h = attitude height of the object from the surface of the Earth.
Hence, acceleration due to gravity decreases with increase in altitude.
Question 9.
On which factors does the escape speed of a body from the surface of Earth depend?
Answer:
The escape speed depends only on the mass and radius of the planet.
[Note: Escape velocity does not depend upon the mass of the body]
Question 10.
As we go from one planet to another planet, how will the mass and weight of a body change?
Answer:
Question 11.
What is periodic time of a geostationary satellite?
Answer:
The periodic time of a geostationary satellite is same as that of the Earth i.e., one day or 24 hours.
Question 12.
State Newton’s law of gravitation and express it in vector form.
Answer:
Question 13.
What do you mean by gravitational constant? State its SI units.
Answer:

Question 14.
Why is a minimum two stage rocket necessary for launching of a satellite?
Answer:
Question 15.
State the conditions for various possible orbits of a satellite depending upon the horizontal speed of projection
Answer:
The path of the satellite depends upon the value of horizontal speed of projection vh relative to critical velocity vc and escape velocity ve.
Case (I) vh < vc:
The orbit of satellite is an ellipse with point of projection as apogee and Earth at one of the foci. During this elliptical path, if the satellite passes through the Earth’s atmosphere. it experiences a nonconservative force of air resistance. As a result it loses energy and spirals down to the Earth.
Case (II) vh = vc:
The satellite moves in a stable circular orbit around the Earth.
Case (III) vc < vh < ve:
The satellite moves in an elliptical orbit round the Earth with the point of projection as perigee.
Case (IV) vh = ve
The satellite travels along parabolic path and never returns to the point of projection. Its speed will be zero at infinity.
Case (V) vh > ve:
The satellite escapes from gravitational influence of Earth traversing a hyperbolic path.
3. Answer the following questions in detail.
Question 1.
Derive an expression for critical velocity of a satellite.
Answer:
Expression for critical velocity:

Question 2.
State any four applications of a communication satellite.
Answer:
Applications of communication satellite:
Question 3.
Show that acceleration due to gravity at height h above the Earth’s surface is gh = g(\(\frac{R}{R+h}\))2
Answer:
Variation of g due to altitude:
Question 4.
Draw a labelled diagram to show different trajectories of a satellite depending upon the tangential projection speed.
Answer:

vh = horizontal speed of projection
v c = critical velocity
ve = escape velocity
Question 5.
Derive an expression for binding energy of a body at rest on the Earth’s surface.
Answer:

Question 6.
Why do astronauts in an orbiting satellite have a feeling of weightlessness?
Answer:
Question 7.
Draw a graph showing the variation of gravitational acceleration due to the depth and altitude from the Earth’s surface.
Answer:

Question 8.
At which place on the Earth’s surface is the gravitational acceleration maximum? Why?
Answer:
Question 9.
At which place on the Earth surface the gravitational acceleration minimum? Why?
Answer:

Question 10.
Define the binding energy of a satellite. Obtain an expression for binding energy of a satellite revolving around the Earth at certain attitude.
Answer:
The minimum energy required by a satellite to escape from Earth ‘s gravitational influence is the binding energy of the satellite.
Expression for binding energy of satellite revolving in circular orbit round the Earth:
Question 11.
Obtain the formula for acceleration due to gravity at the depth ‘d’ below the Earth’s surface.
Answer:
Question 12.
State Kepler’s three laws of planetary motion.
Answer:

Question 13.
State the formula for acceleration due to gravity at depth ‘d’ and altitude ‘h’ Hence show that their ratio is equal to \(\left(\frac{R-d}{R-2 h}\right)\) by assuming that the altitude is very small as compared to the radius of the Earth.
Answer:
Question 14.
What is critical velocity? Obtain an expression for critical velocity of an orbiting satellite. On what factors does it depend?
Answer:
The exact horizontal velocity of projection that must be given to a satellite at a certain height so that it can revolve in a circular orbIt round the Earth is called the critical velocity or orbital velocity (vc).
Expression for critical velocity:
Question 15.
Define escape speed. Derive an expression for the escape speed of an object from the surface of the earth.
Answer:

Question 16.
Describe how an artificial satellite using two stage rocket is launched in an orbit around the Earth.
Answer:
4. Solve the following problems.
Question 1.
At what distance below the surface of the Earth, the acceleration due to gravity decreases by 10% of its value at the surface, given radius of Earth is 6400 km.
Solution:
Given: gd = 90% of g i.e., \(\frac{\mathrm{g}_{\mathrm{d}}}{\mathrm{g}}\) = 0.9,
R = 6400km = 6.4 × 106 m
To find: Distance below the Earth’s surface (d)

At distance 640 km below the surface of the Earth, value of acceleration due to gravity decreases by 10%.
Question 2.
If the Earth were made of wood, the mass of wooden Earth would have been 10% as much as it is now (without change in its diameter). Calculate escape speed from the surface of this Earth.
Solution:

As, we know that the escape speed from surface of the Earth is 11.2 km/s, Substituting value of ve = 11.2 km/s
Vew = 11.2 × \(\frac{1}{\sqrt{10}}=\frac{11.2}{3.162}\)
= 11.2 × \(\frac{1}{3.162}\)
…………… [Taking square root value]
= antilog {log(1 1.2) – Log(3.162)}
= antilog {1.0492 – 0.5000}
= antilog {0.5492} = 3.542
∴ Vew = 3.54km/s
The escape velocity from the surface of wooden Earth is 3.54 km/s.

Question 3.
Calculate the kinetic energy, potential energy, total energy and binding energy of an artificial satellite of mass 2000 kg orbiting at a height of 3600 km above the surface of the Earth.
Given:- G = 6.67 × 10-11 Nm2/kg2
R = 6400 km
M = 6 × 1024 kg
Solution:
Given:- m = 2000 kg, h = 3600 km = 3.6 × 106 m,
G = 6.67 × 10-11 Nm2/kg2
R = 6400 km
M = 6 × 1024 kg
To find: i) Kninetic energy (K.E.)
ii) Potential Energy (P.E.)
iii) Total Energy (T.E.)
iv) Binding Energy (B.E.)

From formula (ii),
P.E. = -2 × 40.02 × 109
= -80.04 × 109 J
From formula (iii),
T.E. = (40.02 × 109) + (-80.02 × 109)
= -40.02 × 109 J
From formula (iv),
B.E.= -(-40.02 × 109)
= 40.02 × 109 J
Kinetic energy of the satellite is 40.02 × 109 J, potential energy is -80.04 × 109 J, total energy is -40.02 × 109 J and binding energy is 40.02 × 109 J.
[Note: Total energy of orbiting satellite is negative.]
Question 4.
Two satellites A and B are revolving around a planet. Their periods of revolution are 1 hour and 8 hours respectively. The radius of orbit of satellite B is 4 × 104 km. find radius of orbit of satellite A .
Solution:
Given: TA = 1 hour, TB = 8 hour,
rB = 4 × 104 km
To find: Radius of orbit of satellite A (rA)

Radius of orbit of satellite A will be 1 × 104 km.
Question 5.
Find the gravitational force between the Sun and the Earth.
Given Mass of the Sun = 1.99 × 1030 kg
Mass of the Earth = 5.98 × 1024 kg
The average distance between the Earth and the Sun = 1.5 × 1011 m.
Solution:
Given: MS = 1.99 × 1030 kg
ME = 5.98 × 1024 kg, R = 1.5 × 1011 m.
To find: Gravitational force between the Sun and the Earth (F)
Formula: F = \(\frac{\mathrm{Gm}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\)
Calculation:As, we know, G = 6.67 × 10-11 N m2/kg2
From formula,

= antilog {(log(6.67) + log( 1.99) + log(5.98) – log(2.25)} × 1021
= antilog {(0.8241) + (0.2989) + (0.7767) – (0.3522)} × 1021
= antilog {1.5475} × 1021
= 35.28 × 1021
= 3.5 × 1022 N
The gravitational force between the Sun and the Earth is 3.5 × 1022 N.

Question 6.
Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 × 1024 kg, R = 6400 km).
Solution:
Given: h = 300 km = 0.3 × 106 m,
M = 5.98 × 1024 kg,
R = 6400km = 6.4 × 106 m
G = 6.67 × 10-11 Nm2/kg2
To find: Acceleration due to gravity at height (gh)
Formula: gh = \(\frac{G M}{(R+h)^{2}}\)
Calculation: From formula,
gh = \(\frac{6.67 \times 10^{-11} \times 5.98 \times 10^{24}}{\left[\left(6.4 \times 10^{6}\right)+\left(0.3 \times 10^{6}\right)\right]^{2}}\)
= \(\frac{6.67 \times 5.98 \times 10^{13}}{(6.7)^{2} \times 10^{12}}\)
6.67 X 10” x 5.98 X iO
= antilog {log(6.67) + log(5.98) – 2log(6.7)} × 10
= antilog{0.8241 + 0.7767 – 2(0.8261)} × 10
= antilog {1.6008 – 1.6522} × 10
= antilog {\(\overline{1}\) .9486} × 10
= 0.8884 × 10 = 8.884 m/s2
Acceleration due to gravity at 300 km will be 8.884 m/s2.
Question 7.
Calculate the speed of a satellite in an orbit at a height of 1000 km from the Earth’s surface. ME = 5.98 × 1024 kg, R = 6.4 × 106 m.
Solution:
Given: h = 1000 km = 1 × 106 m,
ME = 5.98 × 1024 kg, R = 6.4 × 106 m,
G = 6.67 × 10-11 N m2/kg2
To find: Speed of satellite (vc)

Speed of the satellite at height 1000 km is 7.34 × 103 m/s.
Question 8.
Calculate the value of acceleration due to gravity on the surface of Mars if the radius of Mars = 3.4 × 103 km and its mass is 6.4 × 1023 kg.
Solution:
Given:
M = 6.4 × 1023 kg
R = 3.4 × 103 = 3.4 × 106 m,
To find: Acceleration due to gravity on the surface of the Mars (gM)
Formula: g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: As, G = 6.67 × 10-11 N m2/kg2
From formula,
gM = \(\frac{6.67 \times 10^{-11} \times 6.4 \times 10^{23}}{\left(3.4 \times 10^{6}\right)^{2}}=\frac{6.67 \times 6.4}{3.4 \times 3.4}\)
= antilog {log(6.67) + log(6.4) – log(3.4) – log(3.4)}
= antilog {(0.8241) + (0.8062) – (0.5315) – (0.53 15)}
= antilog {0.5673}
= 3.693 m/s2
Acceleration due to gravity on the surface of Mars is 3.693 m/s2.
Question 9.
A planet has mass 6.4 × 1024 kg and radius 3.4 × 106 m. Calculate energy required to remove on object of mass 800 kg from the surface of the planet to infinity.
Solution:
Given: M = 6.4 × 1024 kg, R = 3.4 × 106 m, m = 800 kg
To find: Energy required to remove the object from surface of planet to infinity = B.E.
Formula: B.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\)
Calculation: We know that,
G = 6.67 × 10-11 N m2/kg2
From formula,
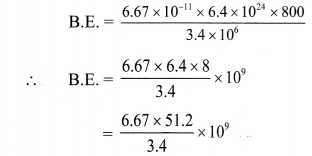
= antilog{log(6.67) + log(51.2) – log(3.4)} × 109
= antilog{0.8241 + 1.7093 – 0.5315} × 109
= antilog {2.0019} × 109
= 1.004 × 102 × 109
= 1.004 × 1011 J
Energy required to remove the object from the surface of the planet is 1.004 × 1011 J.
[Note: Answer calculated above ¡s in accordance with retual methods of calculation.]

Question 10.
Calculate the value of the universal gravitational constant from the given data. Mass of the Earth = 6 × 1024 kg, Radius of the Earth = 6400 km and the acceleration due to gravity on the surface = 9.8 m/s2
Solution:
Given: M = 6 × 1024 kg,
R = 6400km = 6.4 × 106 m,
g = 9.8 m/s2
To find: Gravitational constant (G)
Formula. g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: From formula,
G = \(\frac{\mathrm{gR}^{2}}{\mathrm{M}}\)
G = \(\frac{9.8 \times\left(6.4 \times 10^{6}\right)^{2}}{6 \times 10^{24}}=\frac{401.4 \times 10^{12}}{6 \times 10^{24}}\)
∴ G = 6.69 × 10-11 N m2/kg2
The value of gravitational constant is 6.69 × 10-11 N m2/kg2.
Question 11.
A body weighs 5.6 kg wt on the surface of the Earth. How much will be its weight on a planet whose mass is 1/7 times the mass of the Earth and radius twice that of the Earth’s radius.
Solution:
Given: WE = 5.6 kg-wt.,
\(\frac{\mathrm{M}_{\mathrm{p}}}{\mathrm{M}_{\mathrm{E}}}=\frac{1}{7}, \frac{\mathrm{R}_{\mathrm{p}}}{\mathrm{R}_{\mathrm{E}}}\) = 2
To find: Weight of the body on the surface of planet (Wp)
Formula: W = mg = \(\frac{\mathrm{GMm}}{\mathrm{R}^{2}}\)
Calculation: From formula,
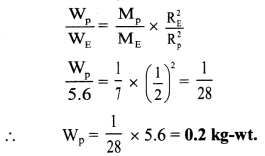
Weight of the body on the surface of a planet will be 0.2 kg-wt.
[Note: The answer given above is calculated in accordance with textual method considering the given data].
Question 12.
What is the gravitational potential due to the Earth at a point which is at a height of 2RE above the surface of the Earth, Mass of the Earth is 6 × 1024 kg, radius of the Earth = 6400 km and G = 6.67 × 10-11 Nm2 kg-2.
Solution:
Given: M = 6 × 1024 kg,
RE = 6400km = 6.4 × 106 m,
G = 6.67 × 10-11 Nm2/kg2,
h = 2RE
To find: Gravitational potential (V)
Formula: V = – \(\frac{\mathrm{GM}}{\mathrm{r}}\)
Calculation: From formula,
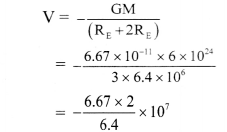
= -2.08 × 107 J kg-1
Negative sign indicates the attractive nature of gravitational potential.
Gravitational potential due to Earth will be 2.08 × 107 J kg-1 towards the centre of the Earth.
[Note: According lo definition of gravitational potential its SI unit is J/kg.]
11th Physics Digest Chapter 5 Gravitation Intext Questions and Answers
Can you recall? (Textbook Page No. 78)
Question 1.
i) What are Kepler’s laws?
ii)What is the shape of the orbits of planets?
Answer:

Question 2.
When released from certain height why do objects tend to fall vertically downwards?
Answer:
When released from certain height, objects tend to fall vertically downwards because of the gravitational force exerted by the Earth.