Balbharti Maharashtra State Board Class 12 Economics Solutions

Chapter 5 Forms of Market Textbook Exercise Questions and Answers.

1. Choose the correct option:

Question 1.
Statements that are incorrect in relation to index numbers.
a) Index number is a geographical tool.
b) Index numbers measure changes in the air pressure.
c) Index numbers measure relative changes in an economic variable.
d) Index numbers are specialized averages.
Options :
1) c and d
2) a and b
3) b and c
4) a and d
Answer:
2) a and b



Question 2.
Statements that highlight the significance of index numbers.
a) Index numbers are useful for making future predictions.
b) Index numbers help in the measurement of inflation.
c) Index numbers help to frame suitable policies.
d) Index numbers can be misused.
Options :
1) b, c and d
2) a, c and d
3) a, b and d
4) a, b and c
Answer:
4) a, b and c

Question 3.
Statements that apply to weighted index
numbers.
a) Every commodity is given equal importance.
b) It assigns suitable ‘weights’ to various commodities.
c) In most of the cases, quantities are used as weights.
d) Laaspeyre’s and Paasche’s method is used in the calculation of weighted index numbers.
Options :
1) b, c and d
2) a, c and d
3) a, b and d
4)a, b, c and d
Answer:
1) b, c and d

Question 4.
Statements related to limitations of index numbers.
a) Index numbers are not completely reliable.
b) There may be a bias in the data collected.
c) Every formula has sorne kind of defect.
d) Index numbers ignore changes in the qualities of products.
Options :
1) a, c and d
2) a, b, c and d
3) a, b and d
4) b, c and d
Answer:
2) a, b, c and d

Question 5.
Choose the correct pair:

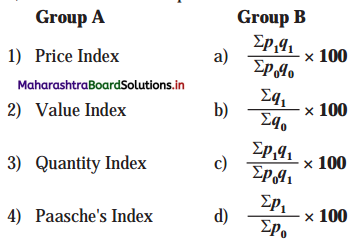
Options :
1) 1-d, 2-c, 3-a, 4-b
2) 1-d, 2-a, 3-b, 4-c
3) 1-b, 2-c, 3-d, 4-a
4) 1-c, 2-d, 3-a, 4-b
Answer:
2) 1-d, 2-a, 3-b, 4-c

2. Complete the Correlation:

1) Price Index: Inflation :: ………………. : Agricultural production
2) ……………….: Base year prices :: P₁ : Current year prices
3) Laaspeyre’s index : ………………. :: Paasches index : Current year quantities
4) ……………….: Single variable :: Composite index: Group of variables
Answers:

3. Solve the following:

Question 1.
Calculate Price Index number from the given data:

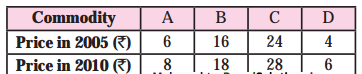
Answer:

Commodity	Base Year price 2005 (P0)	Current Year price 2006 (P1)
A	6	8
B	16	18
C	24	28
D	4	6
Total	Σp0 = 50	Σp1 = 60

Current Year price 2006
(P₁)

Steps:
Add the price of base year (p₀)
Add the price of current year (p₁)
P₀₁ = \(\frac{\Sigma p_{1}}{\Sigma p_{0}}\) x 100
= \(\frac{60}{50}\) x 100
= 120
Hence P₀₁ = 120



Question 2.
Calculate Quantity Index number from the given data:

Answer:

Commodity	Base Year Qty.(q0)	Current Year Qty. (p1)
P	170	90
Q	150	70
R	100	75
S	195	150
T	205	95
Total	Σp0 = 820	Σp1 = 480

Current Year Qty. (p₁₎

Steps : Add quantities of base year (q0).
Add quantities of current year (q ).
Q₀₁ = \(\frac{\Sigma q_{1}}{\Sigma q_{0}}\) x 100
= \(\frac{480}{820}\) x 100
= 58.53
Hence, Q₀₁ = 58.53
As quantity in the current year has fallen Q₀₁ is less than loo.

Question 3.
Calculate Value Index number from the given data:

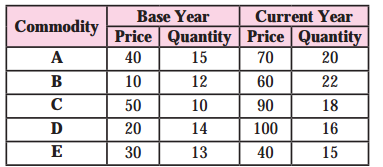
Answer:
Steps:
(1) Formula used for Value Index Number
= V₀₁ = Zpq x 100
(2) We find product of prices and their respective quantities of the different commodities for the base year to derive p0q0, then take the sum total of the products to derive Zp0q0.
(3) Similarly, find the product of prices and their respective quantities for the current year to derive p1q1, then take the sum total of the products to derive p₁q₁.

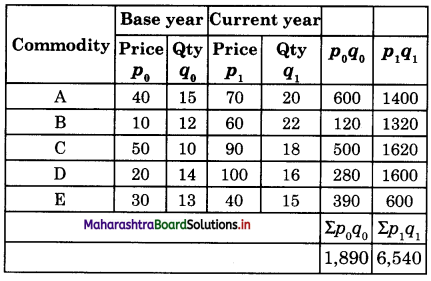
Value Index Number = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{0}}\) x 100
= \(\frac{6,540}{1,890}\) x 100
= 346.03
Value Index Number = 346.03

Question 4.
Calculate Laaspeyre’s and Paasche’s index from the given dala:

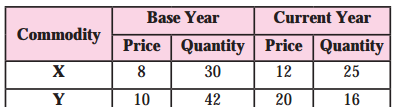
Answer:
I’m 7
Price Index P₀₁ = \(\frac{\Sigma p_{1}}{\Sigma p_{0}}\) x 100
= \(\frac{42}{40}\) x 100
= 105
Hence, P₀₁ = 105

4. Distinguish between:

Question 1.
Simple Index Numbers and Weighted Index Numbers.
Answer:

Simple Index Number	Weighted Index Number
(a) Simple index number is a simple average of index number of individual goods.	(a) Weighted index number is a weighted average of products after assigning suitable weights to individual goods.
(b) It is easy to calculate.	(b) It is difficult to calculate.
(c) All commodities are given equal importance.	(c) All commodities are given different levels of importance.
(d) It gives rough estimates of price change	(d) It gives an accurate estimate of price change.
(e) It is less used in practice.	(e) It is mostly used in practice.

Question 2.
Price Index and Quantity Index.
Answer:

Price Index Number	Quantity Index Number
(a) Price index number measures the changes in price over a period of time.	(a) Quantity index number measures the changes in quantity over a period of time.
(b) It can be used for measuring the changes in prices as well as other purpose e.g. in fixing wages, interest rates, tax rates, etc.	(b) It can be used only for measuring the changes in the quantities e.g. of items like exports, imports, etc.
(c) It is a very popular concept and can be easily calculated and understood.	(c) It is not so popular as it cannot be easily calculated.

Question 3.
Laaspeyre’s Index and Paasche’s Index.
Answer:

Laspeyre’s Index Number	Paasche’s Index Number
(a) Laspeyre uses base year quantity (Q0) as weights to calculate index numbers.	(a) Paasche uses current year quantity (Qt) as weights to calculate index number.
(b) He gave this formula P01 = \( \frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}} \) [where P01 = Price index number p0 = Price of the base year p1 = Price of the current year q0 = Quantities of the base year]	(b) He gave this formula = P01 = \( \frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}} \) [where P01 = Price index number p0 = Price of the base year p1 = Price of the current year q0 = Quantities of the base year]
(c) He is a German Economist who gave the method of calculating Index Number in the year 1871.      .	(c) He is a German Statistician who devised the method of calculating Index Number in the year 1874.

Laspeyre’s Index Number

p₀ = Price of the base year
p₁ = Price of the current year
q₀ = Quantities of the base year]

p₀ = Price of the base year
p₁ = Price of the current year
q₀ = Quantities of the base year]

5. State with reasons whether you agree or disagree with the following statements:

Question 1.
Index numbers measure changes in the price level only.
Answer:
No, I do not agree with this statement.

Question 2.
Index numbers are free from limitations.
Answer:
No, I do not agree with this statement.
Although index numbers are very useful in business and industry, they suffer from following limitation:

Question 3.
Index numbers can be constructed without the base year.
Answer:
No, I do not agree with this statement.
Index numbers can be constructed without the base year because :



6. Answer the following:

Question 1.
Explain the features of index numbers.
Answer:
Features of Index Numbers :

Question 2.
Explain the significance of index numbers in economics
Answer:
Index numbers are significant tools of economic analysis in the following ways:

(1) Help in formulating Policies : Index numbers help the government and business organisations in framing their suitable economic policies for agriculture and industrial sector, wage and dearness allowance policies, etc.

(2) Help in the study of Trends and Tendencies : Index numbers study the relative changes in the level of phenomenon of different periods of time, so they can be used to predict future events. The economists can study the general trends of changes in price levels, agricultural and industrial production, export, imports, etc.

(3) Economic Barometer : Just as barometer is used to measure atmospheric pressure, index numbers measure the level of economic and business behaviour. They are very important for an economist, businessman, planners, policy makers, etc.

(4) Helps in Measurement of Inflation :
It helps the government to take measures against inflation by giving additional D.A. to the employees on the basis of Dearness Index.

(5) Help to adjust National Income : By comparing current year’s national product prices with the base year’s prices, the Domestic Product (GDP) produced. Hence, this shows changes in real national income.

(6) To present Financial Data in Real Income : Index numbers are used to adjust price change, wage change, etc. Thus deflating helps to present the financial data at constant prices.
(Note: Deflating means to make adjustments in the original data)

(7) Helps in determining Depreciation
Cost: The price index helps in determining the depreciation cost of durable goods. At the time of inflation, it is useful to know the original cost of the commodities.



7. Answer in detail:

Question 1.
Explain the steps involved in the construction of index numbers.
Answer:
Steps involved in the construction of j index numbers are as follows :
1. Purpose of an Index Number : Before constructing an index number, one must know the purpose for which the index number is constructed. E.g. for the whole c sale price or retail price or for agricultural – output, etc.

2. Selection of a Base Year : It is important to select a base year against which comparisons are made. So base year or reference year should be
(i) a recent year and not a distant past.
(ii) it should be normal and free from natural calamities, war, etc.

3. Selection of Commodities: When the cost c of living index number of the middle class jj families is to be constructed, the items that are used by middle class families in everyday life should be included and items like big cars, AC’s, etc. should not be included.

4. Selection of Prices : Prices differ from city to city and even from shop to shop in the same city. Hence, we should take a few standard shops from where middle class families buy goods and take the average of the prices of goods sold by them. Otherwise index number
constructed may be misleading.

5. Selection of suitable Average : An ; index number is a special kind of average, Generally arithmetic mean is commonly ? used for construction of index number as it is simple to calculate.

6. Selection of Formula : Number of formulae can be used for construction, of index numbers. Economists have to decide which formula to use for the construction of a particular index number.

7. Assigning proper Weights : Weights refer to the relative importance of different items in the construction of an index number. ( Weights may either be quantity weights (q) or value weights (p). All weights may not be equally important. Therefore, by s assigning specific weights better result can be obtained.

Index Questions

Find out (Textbook Page 58) :

(a) List of crops included in the Index of Agricultural Production in India.
Answer:
Food grains : Rice, Wheat, Jowar, Bajra, Maize, Ragi, Barley and Small Millets. Gram, Tur and other pulses.
Fibres: Cotton, Jute, Mesta and Sannhemp.
Non-food grains : Oilseeds Groundnut, Sesame, Rapeseed and Mustard, Linseed, Castorseed, Safflower, Nigerseed, Soyabean, Sunflower, Coconut and Cottonseed.
Plantation crops: Tea, Coffee and Rubber.
Condiments and Spices : Pepper, Ginger, Garlic, Chillies, Turmeric, Arecanut, Coriander and Cardamom.
Fruits and Vegetables : Potato, Onion, Banana, Cashewnut, Tapioca and Sweet Potato.
Other Crops : Sugarcane, Tobacco and Guarseed.

(b) List of products included in the Index j of Industrial Production in India.
Answer:
Index of Industrial Production in ; India includes – Consumer Durable goods, Consumer non-durable goods, manufacturing goods, mining, electricity, infrastructure or construction goods, etc.

Find out (Textbook Page 59) :

Newspaper headlines related to the following types of index numbers :
(a) Price Index
(b) Agricultural Productivity Index
(c) Index of Industrial Production
(d) Equity Share Price Index
Answer:
[Students should do this activity by themselves.]