Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 3.5 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 3 Circle.

Question 1.
In the adjoining figure, ray PQ touches the circle at point Q. PQ = 12, PR = 8, find PS and RS.
Solution:
i. Ray PQ is a tangent to the circle at point Q and seg PS is the secant. [Given]
∴ PR × PS = PQ² [Tangent secant segments theorem]

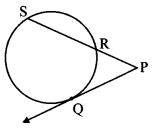
∴ 8 × PS = 12²
∴ 8 × PS = 144
∴ PS = \(\frac { 144 }{ 8 } \)
∴ PS = 18 units
ii. Now, PS = PR + RS [P – R – S]
∴ 18 = 8 + RS
∴ RS = 18 – 8
∴ RS = 10 units

Question 2.
In the adjoining figure, chord MN and chord RS intersect at point D.
i. If RD = 15, DS = 4, MD = 8 find DN
ii. If RS = 18, MD = 9, DN = 8 find DS

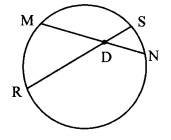
Solution:
i. Chords MN and RS intersect internally at point D. [Given]
∴ MD × DN = RD × DS [Theorem of internal division of chords]
∴ 8 × DN = 15 × 4
∴ DN = \(\frac{15 \times 4}{8}\)
∴ DN = 7.5 units
ii. Let the value of RD be x.
RS = RD + DS [R – D – S]
∴ 18 = x + DS
∴ DS = 18 – x
Now, MD × DN = RD × DS [Theorem of internal division of chords]
∴ 9 × 8 = x(18 – x)
∴ 72 = 18x – x²
∴ x2 – 18x + 72 = 0
∴ x2 – 12x – 6x + 72 = 0
∴ x (x – 12) – 6 (x – 12) = 0
∴ (x – 12) (x – 6) = 0
∴ x – 12 = 0 or x – 6 = 0
∴ x = 12 or x = 6
∴ DS = 18 – 12 or DS = 18 – 6
∴ DS = 6 units or DS = 12 units

Question 3.
In the adjoining figure, O is the centre of the circle and B is a point of contact. Seg OE ⊥ seg AD, AB = 12, AC = 8, find
i. AD
ii. DC
iii. DE.

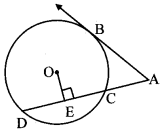
Solution:
i. Line AB is the tangent at point B and seg AD is the secant. [Given]
∴ AC × AD = AB² [Tangent secant segments theorem]
∴ 8 × AD = 122
∴ 8 × AD = 144
∴ AD = \(\frac { 144 }{ 8 } \)
∴ AD = 18 units
ii. AD = AC + DC [A – C – D]
∴ 18 = 8 + DC
∴ DC = 18 – 8
∴ DC = 10 units
iii. seg OE ⊥ seg AD [Given]
i.e. seg OE ⊥ seg CD [A – C – D]
∴ DE = \(\frac { 1 }{ 2 } \) DC [Perpendicular drawn from the centre of the circle to the chord bisects the chord]
= \(\frac { 1 }{ 2 } \) × 10
∴ DE = 5 units

Question 4.
In the adjoining figure, if PQ = 6, QR = 10, PS = 8, find TS.
Solution:
PR = PQ + QR [P-Q-R]
∴ PR = 6 + 10 = 16 units

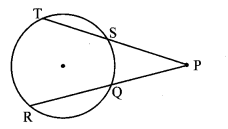
Chords TS and RQ intersect externally at point P.
PQ × PR = PS × PT [Theorem of external division of chords]
∴ 6 × 16 = 8 × PT
∴ PT = \(\frac{6 \times 16}{8}\) = 12 units
But, PT = PS + TS [P – S – T]
∴ 12 = 8 + TS
∴ TS = 12 – 8
∴ TS = 4 units

Question 5.
In the adjoining figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE × GE = 4r².
Given: seg EF is the diameter.
seg DF is a tangent to the circle,
radius = r

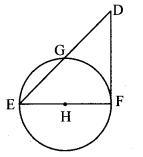
To prove: DE × GE = 4r²
Construction: Join seg GF.
Proof:
seg EF is the diameter. [Given]
∴ ∠EGF = 90° (i) [Angle inscribed in a semicircle]
seg DF is a tangent to the circle at F. [Given]

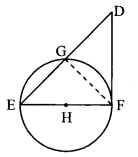
∴ ∠EFD = 90° (ii) [Tangent theorem]
In ∆DFE,
∠EFD = 90 ° [From (ii)]
seg FG ⊥ side DE [From (i)]
∴ ∆EFD ~ ∆EGF [Similarity of right angled triangles]
∴ \(\frac { EF }{ GE } \) = \(\frac { DE }{ EF } \) [Corresponding sides of similar triangles]
∴ DE × GE = EF²
∴ DE × GE = (2r)² [diameter = 2r]
∴ DE × GE = 4r²

Maharashtra Board Class 10 Maths Chapter 3 Circle Intext Questions and Activities

Question 1.
Theorem: If an angle has its vertex on the circle, its one side touches the circle and the other intersects the circle in one more point, then the measure of the angle is half the measure of its intercepted arc. (Textbook pg.no. 75 and 76)

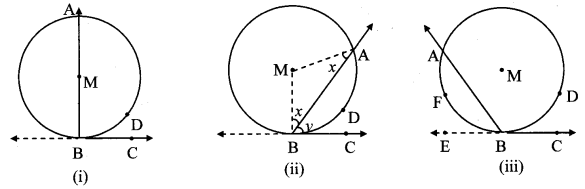
Given: ∠ABC is any angle, whose vertex B lies on the circle with centre M.
Line BC is tangent at B and line BA is secant intersecting the circle at point A.
Arc ADB is intercepted by ∠ABC.
To prove: ∠ABC = \(\frac { 1 }{ 2 } \) m(arc ADB)
Proof:
Case I: Centre M lies on arm BA of ∠ABC.
∠MBC = 90° [Trangnet theorem]

i.e. ∠ABC 90° (i) [A – M – B]
arc ADB is a semicircular arc.
∴ m(arc ADB) = 180° (ii) [Measure ofa semicircle is 180°]
∴ ∠ABC = \(\frac { 1 }{ 2 } \) m(arc ADB) [(From (i) and (ii)]

Case II: Centre M lies in the exterior of ∠ABC.
Draw radii MA and MB.
∴ ∠MBA = ∠MAB [Isosceles triangle theorem]

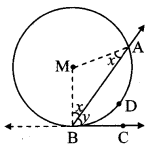
Let, ∠MHA = ∠MAB =x, ∠ABC = y In ∆ABM,
∠AMB + ∠MBA + ∠MAB = 180° [Sum of the measures of all the angles of a triangle is 1800]
∴ ∠AMB + x + x = 180°
∴ ∠AMB = 180° – 2x …… (i)
Now, ∠MBC = ∠MBA + ∠ABC [Angle addition property]
∴ 90° = x + y [Tangent theorem]
∴ x = 90° – y ……(ii)
∠AMB = 180° – 2 (90° – y) [From (i) and (ii)]
∴ ∠AMB = 180° – 180° + 2y
∴ 2y = ∠AMB
∴ y = \(\frac { 1 }{ 2 } \) ∠AMB
∴ ∠ABC = \(\frac { 1 }{ 2 } \) ∠AMB
∴ ∠ABC = \(\frac { 1 }{ 2 } \) m(arc ADB) [Definition of measure of minor arc]

Case III: Centre M lies in the interior of ∠ABC.
Ray BE is the opposite ray of ray BC.
Now, ∠ABE = \(\frac { 1 }{ 2 } \) m (arc AFB) (i) [Proved in case II]

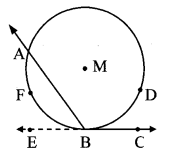
∠ABC + ∠ABE = 180° [Angles in a linear pair]
∴ 180 – ∠ABC = ∠ABE
∴ 180 – ∠ABC = \(\frac { 1 }{ 2 } \) m(arc AFB) [From (i)]
= \(\frac { 1 }{ 2 } \) [360 – m (arc ADB)]
∴ 180 – ∠ABC = 180 – \(\frac { 1 }{ 2 } \) m(arc ADB)
∴ -∠ABC = – \(\frac { 1 }{ 2 } \) m(arc ADB)
∴ ∠ABC = \(\frac { 1 }{ 2 } \) m(arc ADB)

Question 2.
We have proved the above theorem by drawing seg AC and seg DB. Can the theorem be proved by drawing seg AD and seg CB, instead of seg AC and seg DB? (Textbook pg. no. 77)
Solution:
Yes, the theorem can be proved by drawing seg AD and seg CB.
Given: P is the centre of circle, chords AB and CD intersect internally at point E.
To prove: AE × EB = CE × ED
Construction: Draw seg AD and seg CB.

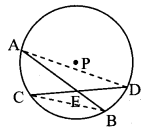
Proof:
In ∆CEB and ∆AED,
∠CEB = ∠DEA [Vertically opposite angles]
∠CBE = ∠ADE [Angles inscribed in the same arc]
∴ ∆CEB ~ ∆AED [by AA test of similarity]
∴ \(\frac { CE }{ AE } \) = \(\frac { EB }{ ED } \) [Corresponding sides of similar triangles]
∴ AE × EB = CE × ED

Question 3.
In figure, seg PQ is a diameter of a circle with centre O. R is any point on the circle, seg RS ⊥ seg PQ. Prove that, SR is the geometric mean of PS and SQ. [That is, SR² = PS × SQ] (Textbook pg. no. 81)
Given: seg PQ is the diameter.
seg RS ⊥ seg PQ
To prove: SR² = PS × SQ
Construction: Extend ray RS, let it intersect the circle at point T.

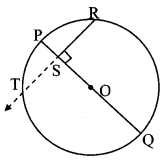
Proof:
seg PQ ⊥ seg RS [Given]
∴ seg OS ⊥ chord RT [R – S – T, P – S – O]
∴ segSR = segTS (i) [Perpendicular drawn from the centre of the circle to the chord bisects the chord]
Chords PQ and RT intersect internally at point S.
∴ SR × TS = PS × SQ [Theorem of internal division of chords]
∴ SR × SR = PS × SQ [From (i)]
∴ SR² = PS × SQ

Question 4.
Theorem: If secants containing chords AB and CD of a circle intersect outside the circle in point E, then
AE × EB = CE × ED. (Textbook pg. no. 78)
Given: Chords AB and CD of a circle intersect outside the circle in point E.
To prove: AE × EB = CE × ED
Construction: Draw seg AD and seg BC.

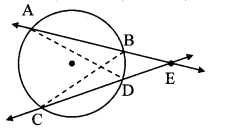
Proof:
In ∆ADE and ∆CBE,
∠AED = ∠CEB [Common angle]
∠DAE ≅ ∠BCE [Angles inscribed in the same arc]
∴ ∆ADE ~ ∆CBE [AA testof similaritv]
∴ \(\frac { AE }{ CE } \) = \(\frac { ED }{ EB } \) [Corresponding sides of similar triangles]
∴ AE × EB = CE × ED

Question 5.
Theorem: Point E is in the exterior of a circle. A secant through E intersects the circle at points A and B, and a tangent through E touches the circle at point T, then EA × EB = ET².
Given: Secant through point E intersects the circle in points A and B.
Tangent drawn through point E touches the circle in point T.
To prove: EA × EB = ET²
Construction: Draw seg TA and seg TB.

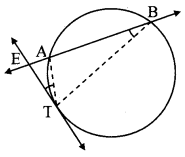
Proof:
In ∆EAT and ∆ETB,
∠AET ≅ ∠TEB [Common angle]
∠ETA ≅ ∠EBT [Theorem of angle between tangent and secant, E – A – B]
∴ ∆EAT ~ ∆ETB [AA test of similarity]
∴ \(\frac { EA }{ ET } \) = \(\frac { ET }{ EB } \) [Corresponding sides of similar triangles]
∴ EA × EB = ET²

Question 6.
In the figure in the above example, if seg PR and seg RQ are drawn, what is the nature of ∆PRQ. (Textbook pg. no, 81)
Answer:
seg PQ is the diameter of the circle.
∴ ∠PRQ = 90°

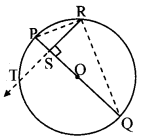
∴ ∆PRQ is a right angled triangle. [Angle inscribed in a semicircle]

Question 7.
Have you previously proved the property proved in the above example? (Textbook pg. no. 81)
Answer:
Yes. It is the theorem of geometric mean.
∆PSR ~ ∆RSQ [Similarity of right angled triangles]

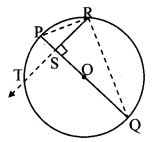
∴ \(\frac { PS }{ SR } \) = \(\frac { SR }{ SQ } \) [Corresponding sides of similar triangles]
∴ SR² = PS × SQ

Loading...

Submit Answer

Show Answer

Hide Answer