Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 7.4 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 7 Mensuration.
10th Standard Maths 2 Practice Set 7.4 Chapter 7 Mensuration Textbook Answers Maharashtra Board
Class 10 Maths Part 2 Practice Set 7.4 Chapter 7 Mensuration Questions With Answers Maharashtra Board
Practice Set 7.4 Geometry Class 10 Question 1. In the adjoining figure, A is the centre of the circle. ∠ABC = 45° and AC = 7\(\sqrt { 2 }\) cm. Find the area of segment BXC, (π = 3.14)
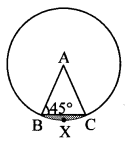
Solution:
In ∆ABC,
AC = AB … [Radii of same circle]
∴ ∠ABC = ∠ACB …[Isosceles triangle theorem]
∴ ∠ABC = ∠ACB = 45°
In ∆ABC,
∠ABC + ∠ACB + ∠BAC = 180° … [Sum of the measures of angles of a triangle is 180° ]
∴ 45° + 45° + ∠BAC = 180°
∴ 90° + ∠BAC = 180°
∴ ∠BAC = 90°
Let ∠BAC = θ = 90°
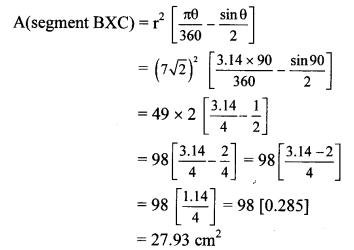
∴ The area of segment BXC is 27.93 cm
2
.
10th Class Geometry Practice Set 7.4 Question 2. In the adjoining figure, O is the centre of the circle.
m(arc PQR) = 60°, OP = 10 cm. Find the area of the shaded region.
(π = 3.14, \(\sqrt { 3 }\) = 1.73)
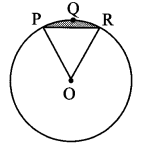
Given: m(arc PQR) = 60°, radius (r) = OP = 10 cm
To find: Area of shaded region.
Solution:
∠POR = m (arc PQR) …[Measure of central angle]
∴ ∠POR = θ = 60°

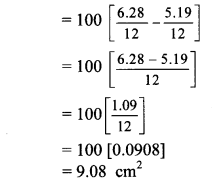
∴ The area of the shaded region is 9.08 cm
2
.
7.4 Class 10 Question 3. In the adjoining figure, if A is the centre of the circle, ∠PAR = 30°, AP = 7.5, find the area of the segment PQR. (π = 3.14)
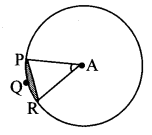
Given: Central angle (θ) = ∠PAR = 30°,
radius (r) = AP = 7.5
To find: Area of segment PQR.
Solution:
Let ∠PAR = θ = 30°
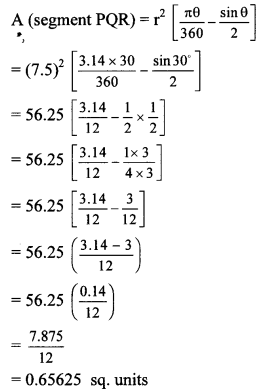
∴ The area of segment PQR is 0.65625 sq. units.
Chapter 7 Maths Class 10 Question 4. In the adjoining figure, if O is the centre of the circle, PQ is a chord, ∠POQ = 90°, area of shaded region is 114 cm2, find the radius of the circle, (π = 3.14)
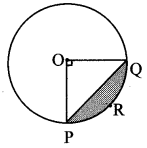
Given: Central angle (θ) = ∠POQ= 90°,
A (segment PRQ) = 114 cm
2
To find: Radius (r).
Solution:
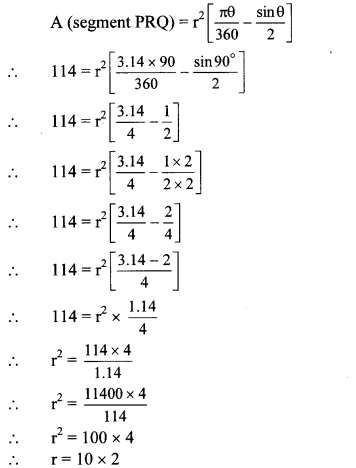
…[Taking square root of both sides]
∴ r = 20 cm
∴ The radius of the circle is 20 cm.
Mensuration Questions for Class 10 Question 5. A chord PQ of a circle with radius 15 cm subtends an angle of 60° with the centre of the circle. Find the area of the minor as well as the major segment. (π = 3.14, \(\sqrt { 3 }\) = 1.73)
Given: Radius (r) =15 cm, central angle (θ) = 60°
To find: Areas of major and minor segments.
Solution:
Let chord PQ subtend ∠POQ = 60° at centre.
∴ θ = 60°
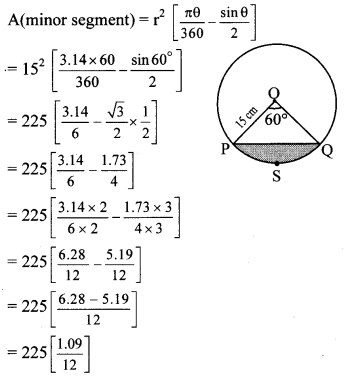
= 225 [0.0908]
= 20.43 cm
2
∴ area of minor segment = 20.43 cm
2
Area of circle = πr
2
= 3.14 × 15 × 15
= 3.14 × 225
= 706.5 cm
2
Area of major segment
= Area of circle – area of minor segment
= 706.5 – 20.43
= 686.07 cm
2
Area of major segment 686.07 cm
2
∴ The area of minor segment Is 20.43 cm
2
and the area of major segment is 686.07 cm
2
.