Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 1.3 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 1 Sets.
Question 1.
If A = {a, b, c, d, e}, B = {c, d, e, f}, C = {b, d}, D = {a, e}, then which of the following statements are true and which are false?
i. C ⊆ 3
ii. A ⊆ D
iii. D ⊆ B
iv. D ⊆ A
V. B ⊆ A
vi. C ⊆ A
Ans:
i. C = {b, d}, B = {c, d, e ,f}
C ⊆ B
False
Since, all the elements of C are not present in B.
ii. A = {a, b, c, d, e}, D = {a, e}
A ⊆ D
False
Since, all the elements of A are not present in D.
iii. D = {a, e}, B = {c, d, e, f}
D ⊆ B
False
Since, all the elements of D are not present in B.
iv. D = {a, e}, A = {a, b, c, d, e}
D ⊆ A
True
Since, all the elements of D are present in A.
v. B = {c, d, e, f}, A = {a, b, c, d, e}
B ⊆ A
False
Since, all the elements of B are not present in A.
vi. C = {b, d}, A= {a, b, c, d, e}
C ⊆A
True
Since, all the elements of C are present in A.
Question 2.
Take the set of natural numbers from 1 to 20 as universal set and show set X and Y using Venn diagram. [2 Marks each]
i. X= {x |x ∈ N, and 7 < x < 15}
ii. Y = { y | y ∈ N, y is a prime number from 1 to 20}
Answer:
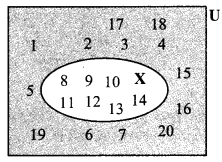
i. U = {1, 2, 3, 4, …….., 18, 19, 20}
x = {x | x ∈ N, and 7 < x < 15}
∴ x = {8, 9, 10, 11, 12, 13, 14}
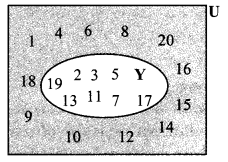
ii. U = {1, 2, 3, 4, …… ,18, 19, 20}
Y = { y | y ∈ N, y is a prime number from 1 to 20}
∴ Y = {2, 3, 5, 7, 11, 13, 17, 19}
Question 3.
U = {1, 2, 3, 7, 8, 9, 10, 11, 12} P = {1, 3, 7,10}, then
i. show the sets U, P and P’ by Venn diagram.
ii. Verify (P’)’ = P
Solution:
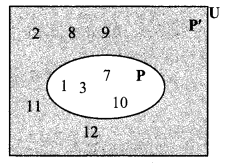
i. Here, U = {1,2, 3, 7, 8,9, 10, 11, 12} P = {1, 3, 7, 10}
∴ P’ = {2, 8, 9, 11, 12}
II. Here, U = {1, 2, 3, 7, 8, 9, 10, 11, 12}
P = {1, 3, 7, 10} ….(i)
∴ P’= {2, 8, 9, 11, 12}
Also, (P’)’ = {1,3,7, 10} …(ii)
∴ (P’)’ = P … [From (i) and (ii)]
Question 4.
A = {1, 3, 2, 7}, then write any three subsets of A.
Solution:
Three subsets of A:
i. B = {3}
ii. C = {2, 1}
iii. D= {1, 2, 7}
[Note: The above problem has many solutions. Students may write solutions other than the ones given]
Question 5.
i. Write the subset relation between the sets.
P is the set of all residents in Pune.
M is the set of all residents in Madhya Pradesh.
I is the set of all residents in Indore.
B is the set of all residents in India.
H is the set of all residents in Maharashtra.
ii. Which set can be the universal set for above sets ?
Solution:
i.
a. The residents of Pune are residents of India.
∴ P ⊆ B
b. The residents of Pune are residents of Maharashtra.
∴ P ⊆ H
c. The residents of Madhya Pradesh are residents of India.
∴ M ⊆ B
d. The residents of Indore are residents of India.
∴ I ⊆ B
e. The residents of Indore are residents of Madhya Pradesh.
∴ I ⊆ M
f. The residents of Maharashtra are residents of India.
∴ H ⊆B
ii. The residents of Pune, Madhya Pradesh, Indore and Maharashtra are all residents of India.
∴ B can be the Universal set for the above sets.
Question 6.
Which set of numbers could be the universal set for the sets given below?
i. A = set of multiples of 5,
B = set of multiples of 7,
C = set of multiples of 12
ii. P = set of integers which are multiples of 4.
T = set of all even square numbers.
Answer:
i. A = set of multiples of 5
∴ A = {5, 10, 15, …}
B = set of multiples of 7
∴ B = {7, 14, 21,…}
C = set of multiples of 12
∴ C = {12, 24, 36, …}
Now, set of natural numbers, whole numbers, integers, rational numbers are as follows:
N = {1, 2, 3, …}, W = {0, 1, 2, 3, …}
I = {…,-3, -2, -1, 0, 1, 2, 3, …}
Q = { \(\frac { p }{ q }\) | p,q ∈ I,q ≠ 0}
Since, set A, B and C are the subsets of sets N, W , I and Q.
∴ For set A, B and C we can take any one of the set from N, W, I or Q as universal set.
ii. P = set of integers which are multiples of 4.
P = {4, 8, 12,…}
T = set of all even square numbers T = {22, 42, 62, …]
Since, set P and T are the subsets of sets N, W, I and Q.
∴ For set P and T we can take any one of the set from N, W, I or Q as universal set.
Question 7.
Let all the students of a class form a Universal set. Let set A be the students who secure 50% or more marks in Maths. Then write the complement of set A.
Answer:
Here, U = all the students of a class.
A = Students who secured 50% or more marks in Maths.
∴ A’= Students who secured less than 50% marks in Maths.
Question 1.
If A = {1, 3, 4, 7, 8}, then write all possible subsets of A.
i. e. P = {1, 3}, T = {4, 7, 8}, V = {1, 4, 8}, S = {1, 4, 7, 8}
In this way many subsets can be written. Write five more subsets of set A. (Textbook pg. no, 8)
Answer:
B = { },
E = {4},
C = {1, 4},
D = {3, 4, 7},
F = {3, 4, 7,8}
Question 2.
Some sets are given below.
A ={…,-4, -2, 0, 2, 4, 6,…}
B = {1, 2, 3,…}
C = {…,-12, -6, 0, 6, 12, 18, }
D = {…, -8, -4, 0, 4, 8,…}
I = {…,-3, -2, -1, 0, 1, 2, 3, 4, }
Discuss and decide which of the following statements are true.
a. A is a subset of sets B, C and D.
b. B is a subset of all the sets which are given above. (Textbook pg. no. 9)
Solution:
a. All elements of set A are not present in set B, C and D.
∴ A ⊆ B,
∴ A ⊆ C,
∴ A ⊆ D
∴ Statement (a) is false.
b. All elements of set B are not present in set A, C and D.
∴ B ⊆ A,
∴ B ⊆ C,
∴ B ⊆ D
∴ Statement (b) is false.
Question 3.
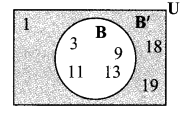
Suppose U = {1, 3, 9, 11, 13, 18, 19}, and B = {3, 9, 11, 13}. Find (B’)’ and draw the inference. (Textbook pg. no. 10)
Solution:
U = {1, 3, 9, 11, 13, 18, 19},
B= {3, 9, 11, 13} ….(i)
∴ B’= {1, 18, 19}
(B’)’= {3, 9, 11, 13} ….(ii)
∴ (B’)’ = B … [From (i) and (ii)]
∴ Complement of a complement is the given set itself.