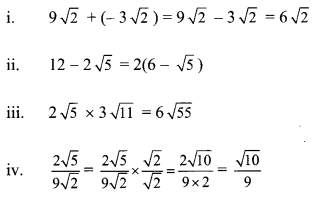Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 2.3 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 2 Real Numbers.
9th Standard Maths 1 Practice Set 2.3 Chapter 2 Real Numbers Textbook Answers Maharashtra Board
Class 9 Maths Part 1 Practice Set 2.3 Chapter 2 Real Numbers Questions With Answers Maharashtra Board
Question 1.
State the order of the surds given below.

Answer:
i. 3, ii. 2, iii. 4, iv. 2, v. 3
Question 2.
State which of the following are surds Justify. [2 Marks each]

Answer:
i. \(\sqrt [ 3 ]{ 51 }\) is a surd because 51 is a positive rational number, 3 is a positive integer greater than 1 and \(\sqrt [ 3 ]{ 51 }\) is irrational.
ii. \(\sqrt [ 4 ]{ 16 }\) is not a surd because
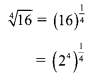
= 2, which is not an irrational number.
iii. \(\sqrt [ 5 ]{ 81 }\) is a surd because 81 is a positive rational number, 5 is a positive integer greater than 1 and \(\sqrt [ 5 ]{ 81 }\) is irrational.
iv. \(\sqrt { 256 }\) is not a surd because
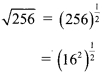
= 16, which is not an irrational number.
v. \(\sqrt [ 3 ]{ 64 }\) is not a surd because
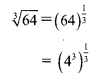
= 4, which is not an irrational number.
vi. \(\sqrt { \frac { 22 }{ 7 } }\) is a surd because \(\frac { 22 }{ 7 }\) is a positive rational number, 2 is a positive integer greater than 1 and \(\sqrt { \frac { 22 }{ 7 } }\) is irrational.
Question 3.
Classify the given pair of surds into like surds and unlike surds. [2 Marks each]

Solution:
If the order of the surds and the radicands are same, then the surds are like surds.
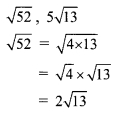
Here, the order of 2\(\sqrt { 13 }\) and 5\(\sqrt { 13 }\) is same and their radicands are also same.
∴ \(\sqrt { 52 }\) and 5\(\sqrt { 13 }\) are like surds.
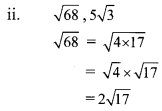
Here, the order of 2\(\sqrt { 17 }\) and 5\(\sqrt { 3 }\) is same but their radicands are not.
∴ \(\sqrt { 68 }\) and 5\(\sqrt { 3 }\) are unlike surds.
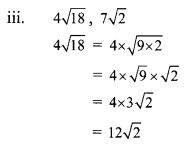
Here, the order of 12\(\sqrt { 2 }\) and 7\(\sqrt { 2 }\) is same and their radicands are also same.
∴ 4\(\sqrt { 18 }\) and 7\(\sqrt { 2 }\) are like surds.
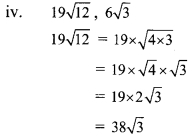
Here, the order of 38\(\sqrt { 3 }\) and 6\(\sqrt { 3 }\) is same and their radicands are also same.
∴ 19\(\sqrt { 12 }\) and 6\(\sqrt { 3 }\) are like surds.
v. 5\(\sqrt { 22 }\), 7\(\sqrt { 33 }\)
Here, the order of 5\(\sqrt { 22 }\) and 7\(\sqrt { 33 }\) is same but their radicands are not.
∴ 5\(\sqrt { 22 }\) and 7\(\sqrt { 33 }\) are unlike surds.
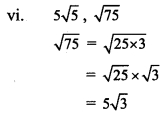
Here, the order of 5√5 and 5√3 is same but their radicands are not.
∴ 5√5 and √75 are unlike surds.
Question 4.
Simplify the following surds.
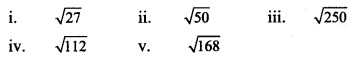
Solution:
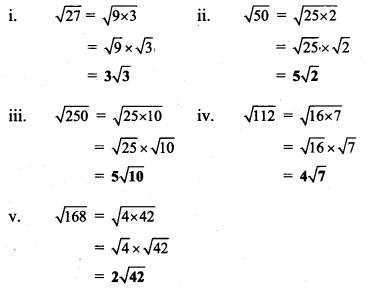
Question 5.
Compare the following pair of surds.
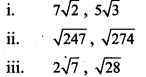

Solution:


Question 6.
Simplify.
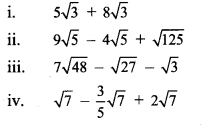
Solution:
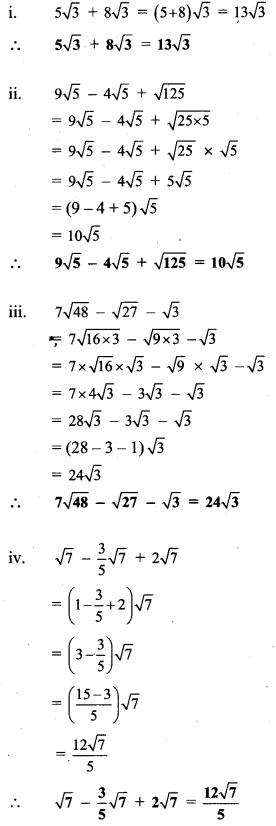
Question 7.
Multiply and write the answer in the simplest form.
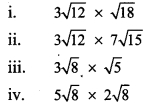
Solution:
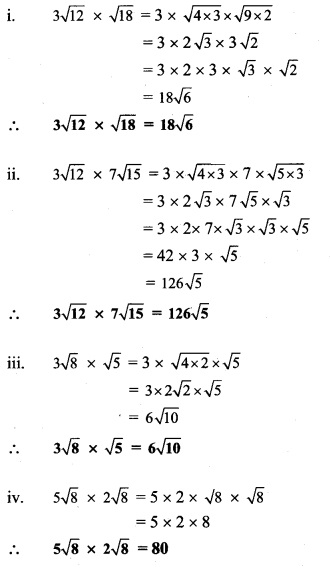
Question 8.
Divide and write form.
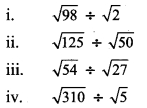
Solution:
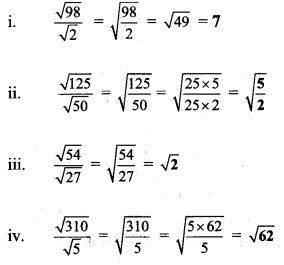
Question 9.
Rationalize the denominator.
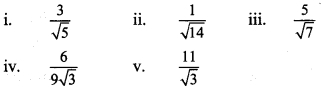
Solution:


Question 1.
\(\sqrt { 9+16 }\) ? + \(\sqrt { 9 }\) + \(\sqrt { 16 }\) (Texbookpg. no. 28)
Solution:
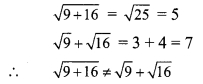
Question 2.
\(\sqrt { 100+36 }\) ? \(\sqrt { 100 }\) + \(\sqrt { 36 }\) (Textbook pg. no. 28)
Solution:
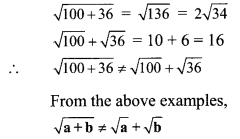
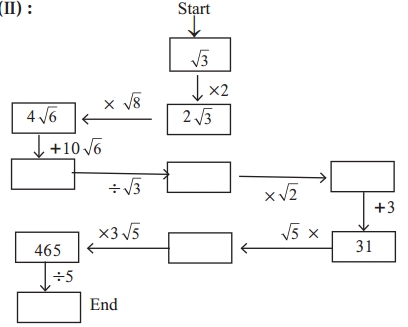
Question 3.
Follow the arrows and complete the chart by doing the operations given. (Textbook pg. no. 34)
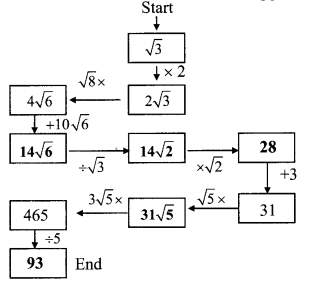
Solution:
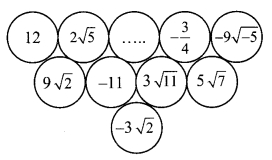
Question 4.
There are some real numbers written on a card sheet. Use these numbers and construct two examples each of addition, subtraction, multiplication and division. Solve these examples. (Textbook pg. no. 34)
Solution: