Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.4 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.
Question 1.
Fill in the blanks of the following.
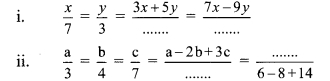
Solution:

Question 2.
5m – n = 3m + 4n, then find the values of the following expressions.
![]()
Solution:
5m – n = 3m + 4n … [Given]
∴ 5m – 3m = 4n + n
∴ 2m = 5n
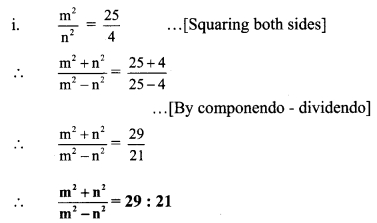

Question 3.
Solve:
i. If a(y + z) = b(z + x) = c(x + y) and out of a, b, c no two of them are equal, then show that, \( \frac{y-z}{a(b-c)}=\frac{z-x}{b(c-a)}=\frac{x-y}{c(a-b)}\).
Solution:
Here, no two of a, b and c are equal.
∴ values of (b – c), (c – a) and (a – b) are not zero.
a(y + z) = b(z + x) = c(x + y) … [Given]
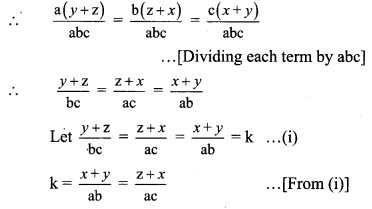

ii. If \(\frac{x}{3 x-y-z}=\frac{y}{3 y-z-x}=\frac{z}{3 z-x-y}\) and x + y + z ≠ 0, then show that the value of each ratio is equal to 1.
Solution:

iii. \(\frac{x}{3 x-y-z}=\frac{y}{3 y-z-x}=\frac{z}{3 z-x-y}\) and x + y + z ≠ 0,then show that \(\frac { a+b }{ 2 }\).
Solution:
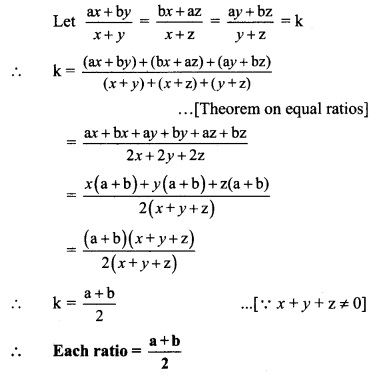
iv. If \(\frac{y+z}{a}=\frac{z+x}{b}=\frac{x+y}{c}\) , then show that \(\frac{x}{b+c-a}=\frac{y}{c+a-b}=\frac{z}{a+b-c}\).
Solution:


v. If \(\frac{3 x-5 y}{5 z+3 y}=\frac{x+5 z}{y-5 x}=\frac{y-z}{x-z}\) , then show that every ratio = \(\frac { x }{ y }\).
Solution:

Ratio And Proportion Class 9 Practice Set 4.4 Question 4.
Solve:
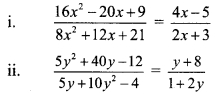
Solution:
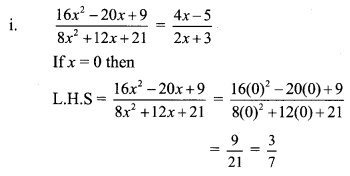

∴ 7(4x – 5)3(2x + 3)
∴ 28x – 35 = 6x + 9
∴ 28x – 6x = 9 + 35
∴ 22x = 44
∴ x = 2
∴ x = 2 is the solution of the given equation.
ii. \(\frac{5 y^{2}+40 y-12}{5 y+10 y^{2}-4}=\frac{y+8}{1+2 y}\)


∴ y + 8 = 3(1 + 2y)
∴ y + 8 = 3 + 6y
∴ 8 – 3 = 6y – y
∴ 5 = 5y
∴ y = 1
∴ y = 1 is the solution of the given equation.