Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 2.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 2 Parallel Lines.
9th Standard Maths 2 Practice Set 2.1 Chapter 2 Parallel Lines Textbook Answers Maharashtra Board
Class 9 Maths Part 2 Practice Set 2.1 Chapter 2 Parallel Lines Questions With Answers Maharashtra Board
Question :
In the given figure, line RP || line MS and line DK is their transversal. ∠DHP = 85°. Find the measures of following angles.
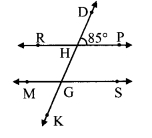
i. ∠RHD
ii. ∠PHG
iii. ∠HGS
iv. ∠MGK
Solution:
i. ∠DHP = 85° …..(i)
∠DHP + ∠RHD = 180° [Angles in a linear pair]
85° + ∠RHD = 180°
∴ ∠RHD = 180°- 85°
∴ ∠RHD = 95° …..(ii)
ii. ∠PHG = ∠RHD [Vertically opposite angles]
∴ ∠PHG = 95° [From (ii)]
iii. line RP || line MS and line DK is their transversal. [Corresponding angles]
∴ ∠HGS = ∠DHP …..(iii) [From (i)]
iv. ∠HGS = 85° [Vertically opposite angles]
∴ ∠MGK = ∠HGS ∠MGK = 85° [From (iii)]
Question 2.
In the given figure line p line q and line l and line m are tranversals.
Measures of some angles are shown. Hence find the measures of ∠a, ∠b, ∠c, ∠d.
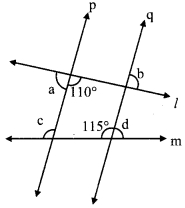
Solution:
i. 110 + ∠a = 180° [Angles in a linear pair]
∴ ∠a = 180° – 110°
∴ ∠a = 70°
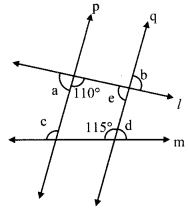
ii. consider ∠e as shown in the figure line p || line q, and line lis their transversal.
∠e + 110° = 180° [Interior angles]
∴ ∠e = 180° – 110°
∴ ∠e = 70°
But, ∠b = ∠e [Vertically opposite angles]
∴ ∠b = 70°
iii. line p || line q, and line m is their transversal.
∴ ∠c = 115° [Corresponding angles]
iv. 115° + ∠d = 180° [Angles in a linear pair]
∴ ∠d = 180° – 115°
∴ ∠d = 65°
Question 3.
In the given figure, line 11| line m and line n || line p. Find ∠a, ∠b, ∠c from the given measure of an angle.
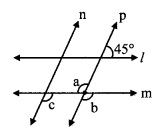
Solution:
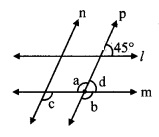
i. consider ∠d as shown in the figure
line l || line m, and line p is their transversal.
∴ ∠d = 45° [Corresponding angles]
Now, ∠d + ∠b = 180° [Angles in a linear pair]
∴ 45° +∠b = 180°
∴ ∠b = 180° – 45°
∴ ∠b = 135° …..(i)
ii. ∠a = ∠b [Vertically opposite angles]
∴ ∠a = 135° [From (i)]
iii. line n || line p, and line m is their transversal.
∴ ∠c = ∠b [Corresponding angles]
∴ ∠c = 135° [From (i)]
Question 4.
In the given figure, sides of ∠PQR and ∠XYZ are parallel to each other. Prove that, ∠PQR ≅ ∠XYZ.
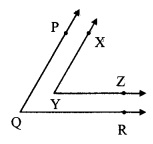
Given: Ray YZ || ray QRandray YX || ray QP
To prove: ∠PQR ≅ ∠XYZ
Construction: Extend ray YZ in the opposite direction. It intersects ray QP at point S.
Solution:
Proof:
Ray YX || ray QP [Given]
Ray YX || ray SP and seg SY is their transversal [P-S-Q]
∴ ∠XYZ ≅ ∠PSY ……(i) [Corresponding angles]
ray YZ || ray QR [Given]
ray SZ || ray QR and seg PQ is their transversal. [S-Y-Z]
∴ ∠PSY ≅ ∠SQR [Corresponding angles]
∴ ∠PSY ≅ ∠PQR …….. (ii) [P-S-Q]
∴ ∠PQR ≅ ∠XYZ [From (i) and (ii)]
Question 5.
In the given figure, line AB || line CD and line PQ is transversal. Measure of one of the angles is given. Hence find the measures of the following angles.
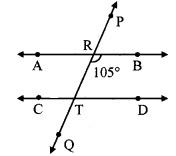
i. ∠ART
ii. ∠CTQ
iii. ∠DTQ
iv. ∠PRB
Solution:
i. ∠BRT = 105° ….(i)
∠ART + ∠BRT = 180° [Angles in a linear pair]
∴ ∠ART + 105° = 180°
∴ ∠ART = 180° – 105°
∴ ∠ART = 75° …(ii)
ii. line AB || line CD and line PQ is their transversal.
∴ ∠CTQ = ∠ART [Corresponding angles]
∴ ∠CTQ = 75° [From (ii)]
iii. line AB || line CD and line PQ is their transversal.
∴ ∠DTQ = ∠BRT [Corresponding angles]
∴ ∠DTQ = 105° [From (i)]
iv. ∠PRB = ∠ART [Vertically opposite angles]
∴ ∠PRB = 75° [From (ii)]
Maharashtra Board Class 9 Maths Chapter 2 Parallel Lines Practice Set 2.1 Intext Questions and Activities
Question 1.
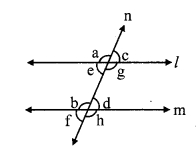
Angles formed by two lines and their transversal. (Textbook pg, no. 13)
When a transversal (line n) intersects two lines (line l and m) in two distinct points, 8 angles are formed as shown in the figure. Pairs of angles formed out of these angles are as follows:
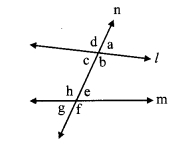
Pairs of corresponding angles
i. ∠d, ∠h
ii. ∠a, ∠e
iii. ∠c, ∠g
iv. ∠b, ∠f
Pairs of alternate interior angles
i. ∠c, ∠e
ii. ∠b, ∠h
Pairs of alternate exterior angles
i. ∠d, ∠f
ii. ∠a, ∠g
Pairs of interior angles on the same side of the transversal
i. ∠c, ∠h
ii. ∠b, ∠e
Some important properties:
1. When two lines intersect, the pairs of vertically opposite angles formed are congruent.
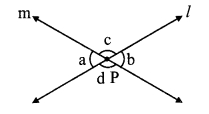
Example:
In the given diagram,
line l and m intersect at point P.
The pairs of vertically opposite angles that are congruent are:
i. ∠a ≅ ∠b
ii. ∠c ≅ ∠d
2. The angles in a linear pair are supplementary.
Example:
For the given diagram,
∠a and ∠c are in linear pair
∴ ∠a + ∠c = 180°
Also, ∠d and ∠b are in linear pair
∴ ∠d + ∠b = 180°
3. When one pair of corresponding angles is congruent, then all the remaining pairs of corresponding angles are congruent.
Example:
In the given diagram,
If ∠a ≅ ∠b
then ∠e ≅ ∠f, ∠c ≅ ∠d and ∠g ≅ ∠h
4. When one pair of alternate angles is congruent, then all the remaining pairs of alternate angles are congruent.
Example:
For the given diagram,
If ∠e ≅ ∠d, then ∠g ≅ ∠b
Also, ∠a ≅ ∠h and ∠c ≅ ∠f
5. When one pair of interior angles on one side of the transversal is supplementary, then the other pair of interior angles is also supplementary.
Example:
For the given diagram,
If ∠e + ∠b = 180°, then ∠g + ∠d = 180°.