Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 3.3 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 3 Triangles.
Question 1.
Find the values of x and y using the information shown in the given figure. Find the measures of ∠ABD and ∠ACD.
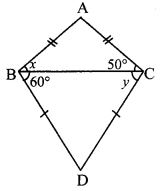
Solution:
i. ∠ACB = 50° [Given]
In ∆ABC, seg AC ≅ seg AB [Given]
∴ ∠ABC ≅ ∠ACB [Isosceles triangle theorem]
∴ x = 50°
ii. ∠DBC = 60° [Given]
In ABDC, seg BD ≅ seg DC [Given]
∴ ∠DCB ≅ ∠DBC [Isosceles triangle theorem]
∴ y = 60°
iii. ∠ABD = ∠ABC + ∠DBC [Angle addition property]
= 50° + 60°
∴ ∠ABD = 110°
iv. ∠ACD = ∠ACB + ∠DCB [Angle addition property]
= 50° + 60°
∴ ∠ACD = 110°
∴ x = 50°, y = 60°,
∠ABD = 110°, ∠ACD = 110°
Question 2.
The length of hypotenuse of a right angled triangle is 15. Find the length of median on its hypotenuse.
Solution:
Length of hypotenuse = 15 [Given]
Length of median on the hypotenuse = \(\frac { 1 }{ 2 }\) x length of hypotenuse [In a right angled triangle, the length of the median on the hypotenuse is half the length of the hypotenuse]
= \(\frac { 1 }{ 2 }\) x 15 = 7.5
∴ The length of the median on the hypotenuse is 7.5 units.
Question 3.
In ∆PQR, ∠Q = 90°, PQ = 12, QR = 5 and QS is a median. Find l(QS).
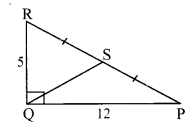
Solution:
i. PQ = 12, QR = 5 [Given]
In APQR, ∠Q = 90° [Given]
∴ PR2 = QR2 + PQ2 [Pythagoras theorem]
= 25 + 144
∴ PR2 =169
∴ PR = 13 units [Taking square root of both sides]
ii. In right angled APQR, seg QS is the median on hypotenuse PR.
∴ QS = \(\frac { 1 }{ 2 }\)PR [In a right angled triangle, the length of the median on the hypotenuse is half the length of the hypotenuse]
= \(\frac { 1 }{ 2 }\) x 13
∴ l(QS) = 6.5 units
Question 4.
In the given figure, point G is the point of concurrence of the medians of ∆PQR. If GT = 2.5, find the lengths of PG and PT.
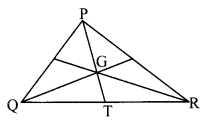
Solution:
i. In ∆PQR, G is the point of concurrence of the medians. [Given]
The centroid divides each median in the ratio 2 : 1.
PG : GT = 2 : 1
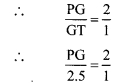
∴ PG = 2 x 2.5
∴ PG = 5 units
ii. Now, PT = PG + GT [P – G – T]
= 5 + 2.5
∴ l(PG) = 5 units, l(PT) = 7.5 units
Maharashtra Board Class 9 Maths Chapter 3 Triangles Practice Set 3.3 Intext Questions and Activities
Question 1.
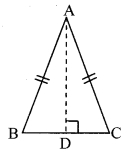
Can the theorem of isosceles triangle be proved by doing a different construction? (Textbook pg. no.34)
Solution:
Yes
Construction: Draw seg AD ⊥ seg BC.
Proof:
In ∆ABD and ∆ACD,
seg AB≅ seg AC [Given]
∠ADB ≅ ∠ADC [Each angle is of measure 90°]
seg AD ≅ seg AD [Common side]
∴ ∆ABD ≅ ∆ACD [Hypotenuse side test]
∴ ∠ABD ≅ ∠ACD [c.a.c.t.]
∴ ∠ABC ≅ ∠ACB [B-D-C]
Question 2.
Can the theorem of isosceles triangle be proved without doing any construction? (Textbook pg, no.34)
Solution:
Yes
Proof:
In ∆ABC and ∆ACB,
seg AB ≅ seg AC [Given]
∠BAC ≅ ∠CAB [Common angle]
seg AC ≅ seg AB [Given]
∴ ∆ABC ≅ ∆ACB [SAS test]
∴ ∠ABC ≅ ∠ACB [c. a. c. t.]
Question 3.
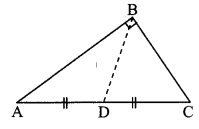
In the given figure, ∆ABC is a right angled triangle, seg BD is the median on hypotenuse. Measure the lengths of the following segments.
i. AD
ii. DC
iii. BD
From the measurements verify that BD = \(\frac { 1 }{ 2 }\)AC. (Textbook pg. no. 37)
Solution:
AD = DC = BD= 1.9 cm
AC = AD + DC [A – D – C]
= 1.9 + 1.9
= 2 x 1.9 cm
∴ AC = 2 x BD
∴ BD = \(\frac { 1 }{ 2 }\) AC