Decimal Fractions Class 5 Problem Set 36 Question Answer Maharashtra Board
Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 9 Decimal Fractions Problem Set 36 Textbook Exercise Important Questions and Answers.
Std 5 Maths Chapter 9 Decimal Fractions
Write the following mixed fractions in decimal form and read them aloud.
\(\text { (1) } 3 \frac{9}{10}\)
Answer:
3.9, Three-point nine.

\(\text { (2) } 1 \frac{4}{10}\)
Answer:
1.4, One point four.
\(\text { (3) } 5 \frac{3}{10}\)
Answer:
5.3, Five-point three.
\(\text { (4) } \frac{8}{10}\)
Answer:
0.8, Zero points eight.
\(\text { (5) } \frac{7}{10}\)
Answer:
0.5, Zero points five.

Hundredths
If \(\frac{1}{10}\) is divided into 10 equal parts, each part becomes \(\frac{1}{100}\) or one hundredth. Therefore, note that 1 tenth =10 hundredths, or 0.1=0.10. By multiplying \(\frac{1}{100}\) by 10 we get \(\frac{10}{100}\) = \(\frac{1}{10}\). Therefore, it is possible to create a hundredths place next to the tenths place. After creating a hundredths place we can write \(\frac{14}{100}\) as 0.14.
\(\frac{14}{100}=\frac{10+4}{100}=\frac{10}{100}+\frac{4}{100}=\frac{1}{10}+\frac{4}{100}\) meaning that when writing \(\frac{14}{100}\) in decimal form, 1 is written in the tenths place and 4 is written in the hundredths place. This fraction is written as 0.14 and is read as ‘zero point one four’. Similarly, 6 \(\frac{57}{100}\) is written as 6.57 and 50 \(\frac{71}{100}\) is written as 50.71.
While writing \(\frac{3}{100}\) in decimal form, we must remember that there is no number in the tenths place and so, we put 0 in that place, which means that \(\frac{3}{100}\) is written as 0.03.
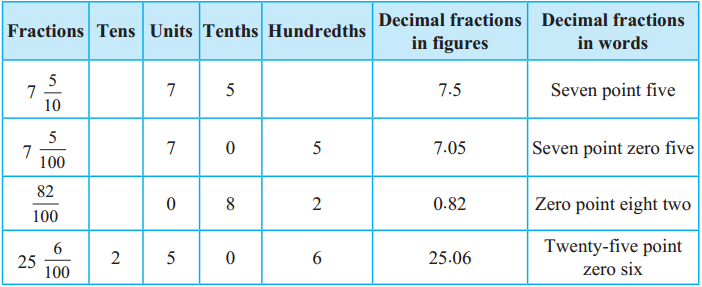
Study how the decimal fractions in the table below are written and read.

Decimal Fractions Problem Set 36 Additional Important Questions and Answers
\(\text { (1) } 4 \frac{6}{10}\)
Answer:
4.6, Four point six. 7
\(\text { (2) } 4 \frac{6}{10}\)
Answer:
2.7, Two point seven.
\(\text { (3) } 4 \frac{6}{10}\)
Answer:
6.2, Six points two.
\(\text { (4) } 4 \frac{6}{10}\)
Answer:
21.1, Twenty-one point one.

\(\text { (5) } 4 \frac{6}{10}\)
Answer:
17.5, Seventeen points five.