Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.1 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 1 Linear Equations in Two Variables.
10th Standard Maths 1 Practice Set 1.1 Chapter 1 Linear Equations in Two Variables Textbook Answers Maharashtra Board
Class 10 Maths Part 1 Practice Set 1.1 Chapter 1 Linear Equations in Two Variables Questions With Answers Maharashtra Board
Question 1.
Complete the following activity to solve the simultaneous equations.
5x + 3y = 9 …(i)
2x-3y=12 …(ii)
Solution:
5x + 3y = 9 …(i)
2x-3y=12 …(ii)
Add equations (i) and (ii).

Question 2.
Solve the following simultaneous equations.
i. 3a + 5b = 26; a + 5b = 22
ii. x + 7y = 10; 3x – 2y = 7
iii. 2x – 3y = 9; 2x + y = 13
iv. 5m – 3n = 19; m – 6n = -7
v. 5x + 2y = -3;x + 5y = 4
vi. \(\frac { 1 }{ 3 } \) x+ y = \(\frac { 10 }{ 3 } \) ; 2x + \(\frac { 1 }{ 4 } \) y = \(\frac { 11 }{ 4 } \)
vii. 99x + 101y = 499 ; 101x + 99y = 501
viii. 49x – 57y = 172; 57x – 49y = 252
Solution:
i. 3a + 5b = 26 …(i)
a + 5b = 22 …(ii)
Subtracting equation (ii) from (i), we get

Substituting a = 2 in equation (ii), we get
2 + 5b = 22
∴ 5b = 22 – 2
∴ 5b = 20
∴ b = \(\frac { 20 }{ 5 } \) =4
∴ (a, b) = (2, 4) is the solution of the given simultaneous equations.
ii. x + 7y = 10
∴ x = 10 – 7y …(i)
3x – 2y = 7 …1(ii)
Substituting x = 10 – ly in equation (ii), we get
3 (10 – 7y) – 2y = 7
∴ 30 – 21y – 2y = 7
∴ -23y = 7 – 30
∴ -23y = -23
∴ y = \(\frac { -23 }{ -23 } \)
Substituting y = 1 in equation (i), we get
x = 10 – 7 (1)
= 10 – 7 = 3
∴ (x, y) = (3, 1) is the solution of the given simultaneous equations.
iii. 2x – 3y = 9 …(i)
2x + y = 13 …(ii)
Subtracting equation (ii) from (i), we get
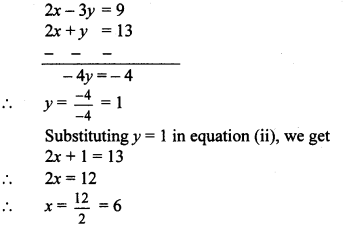
∴ (x, y) = (6, 1) is the solution of the given simultaneous equations.
iv. 5m – 3n = 19 …(i)
m – 6n = -7
∴ m = 6n – 7 …(ii)
Substituting m = 6n – 7 in equation (i), we get
5(6n – 7) – 3n = 19
∴ 30n – 35 – 3n = 19
∴ 27n = 19 + 35
∴ 27n = 54
∴ n = \(\frac { 54 }{ 27 } \) = 2
Substituting n = 2 in equation (ii), we get
m = 6(2) – 7
= 12 – 7 = 5
∴ (m, n) = (5, 2) is the solution of the given simultaneous equations.
v. 5x + 2y = -3 …(i)
x + 5y = 4
∴ x = 4 – 5y …(ii)
Substituting x = 4 – 5y in equation (i), we get
5(4 – 5y) + 2y = -3
∴ 20 – 25y + 2y = -3
∴ -23y = -3 – 20
∴ -23y = -23
∴ y = \(\frac { -23 }{ -23 } \) = 1
Substituting y = 1 in equation (ii), we get
x = 4 – 5(1)
= 4 – 5 = -1
∴ (x, y) = (-1, 1) is the solution of the given simultaneous equations.

Substituting y = 3 in equation (i), we get
x = 10 – 3(3)
= 10 – 9 = 1
∴ (x, y) = (1, 3) is the solution of the given simultaneous equations.
vii. 99x + 101 y = 499 …(i)
101 x + 99y = 501 …(ii)
Adding equations (i) and (ii), we get

Substituting x = 3 in equation (iii), we get
3 + y = 5
∴ y = 5 – 3 = 2
∴ (x, y) = (3, 2) is the solution of the given simultaneous equations.
viii. 49x – 57y = 172 …(i)
57x – 49y = 252 …(ii)
Adding equations (i) and (ii), we get

Substituting x = 7 in equation (iv), we get
7 + y = 10
∴ y = 10 – 7 = 3
∴ (x, y) = (7, 3) is the solution of the given simultaneous equations.
Complete the following table. (Textbook pg. no. 1)

Question 1.
Solve: 3x+ 2y = 29; 5x – y = 18 (Textbook pg. no. 3)
Solution:
3x + 2y = 29 …(i)
and 5x- y = 18 …(ii)
Let’s solve the equations by eliminating ‘y’.
Fill suitably the boxes below.
Multiplying equation (ii) by 2, we get
