Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 2.3 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 2 Quadratic Equations.
10th Standard Maths 1 Practice Set 2.3 Chapter 2 Quadratic Equations Textbook Answers Maharashtra Board
Class 10 Maths Part 1 Practice Set 2.3 Chapter 2 Quadratic Equations Questions With Answers Maharashtra Board
Question 1.
Solve the following quadratic equations by completing the square method.
1. x
2
+ x – 20 = 0
2. x
2
+ 2x – 5 = 0
3. m
2
– 5m = -3
4. 9y
2
– 12y + 2 = 0
5. 2y
2
+ 9y + 10 = 0
6. 5x
2
= 4x + 7
Solution:
1. x
2
+ x – 20 = 0
If x
2
+ x + k = (x + a)
2
, then
x
2
+ x + k = x
2
+ 2ax + a
2
Comparing the coefficients, we get
1 = 2a and k = a
2

∴ The roots of the given quadratic equation are 4 and -5.
2. x
2
+ 2x – 5 = 0
If x
2
+ 2x + k = (x + a)
2
, then
x
2
+ 2x + k = x
2
+ 2ax + a
2
Comparing the coefficients, we get
2 = 2a and k = a
2
∴ a = 1 and k = (1)
2
= 1
Now, x
2
+ 2x – 5 = 0
∴ x
2
+ 2x + 1 – 1 – 5 = 0
∴ (x + 1)
2
– 6 = 0
∴ (x + 1)
2
= 6
Taking square root of both sides, we get
x + 1 = ± √6
∴ x + 1 √6 or x + 1 = √6
∴ x = √6 – 1 or x = -√6 – 1
∴ The roots of the given quadratic equation are √6 -1 and – √6 -1.
3. m
2
– 5m = -3
∴ m
2
– 5m + 3 = 0
If m
2
– 5m + k = (m + a)
2
, then
m
2
– 5m + k = m
2
+ 2am + a
2
Comparing the coefficients, we get
-5 = 2a and k = a
2

4. 9y
2
– 12y + 2 = 0
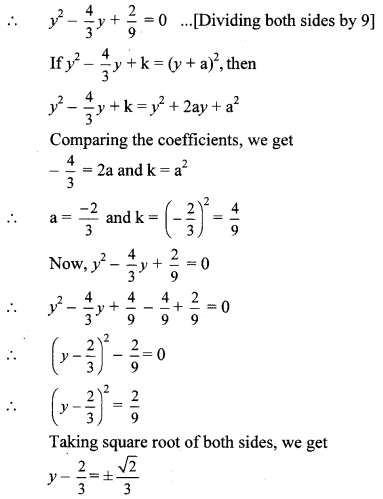
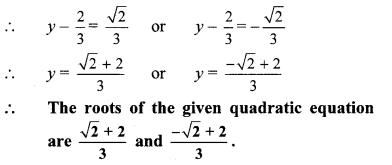
5. 2y
2
+ 9y + 10 = 0
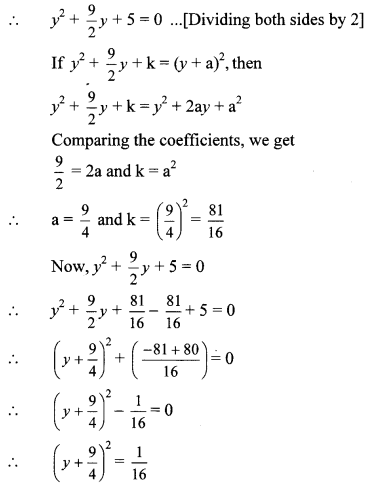
Taking square root of both sides, we get
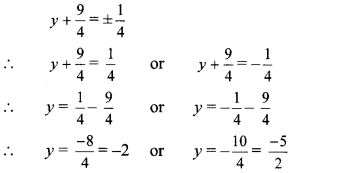
∴ The roots of the given quadratic equation are -2 and \(\frac { -5 }{ 2 } \).
6. 5x
2
= 4x + 7
∴ 5x
2
– 4x – 7 = 0
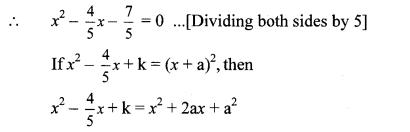
Comparing the coefficients, we get
