Practice Set 1.1 Geometry 10th Standard Maths Part 2 Chapter 1 Similarity Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 1.1 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 1 Similarity.

10th Standard Maths 2 Practice Set 1.1 Chapter 1 Similarity Textbook Answers Maharashtra Board

Class 10 Maths Part 2 Practice Set 1.1 Chapter 1 Similarity Questions With Answers Maharashtra Board

Question 1.
Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.
Solution:
Let the base, height and area of the first triangle be b ₁ , h ₁ , and A ₁ respectively.
Let the base, height and area of the second triangle be b ₂ , h ₂ and A ₂ respectively.

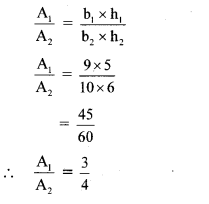
[Since Ratio of areas of two triangles is equal to the ratio of the product of their bases and corresponding heights]
∴ The ratio of areas of the triangles is 3:4.

Question 2.
In the adjoining figure, BC ± AB, AD _L AB, BC = 4, AD = 8, then find \(\frac{A(\Delta A B C)}{A(\Delta A D B)}\)

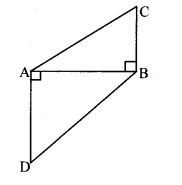
Solution:
∆ABC and ∆ADB have same base AB.

[Since Triangles having equal base]

Question 3.
In the adjoining figure, seg PS ± seg RQ, seg QT ± seg PR. If RQ = 6, PS = 6 and PR = 12, then find QT.

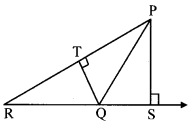
Solution:
In ∆PQR, PR is the base and QT is the corresponding height.
Also, RQ is the base and PS is the corresponding height.
\(\frac{A(\Delta P Q R)}{A(\Delta P Q R)}=\frac{P R \times Q T}{R Q \times P S}\) [Ratio of areas of two triangles is equal to the ratio of the product of their bases and corresponding heights]
∴ \(\frac{1}{1}=\frac{P R \times Q T}{R Q \times P S}\)
∴ PR × QT = RQ × PS
∴ 12 × QT = 6 × 6
∴ QT = \(\frac { 36 }{ 12 } \)
∴ QT = 3 units

Question 4.
In the adjoining figure, AP ⊥ BC, AD || BC, then find A(∆ABC) : A(∆BCD).

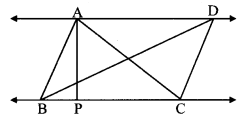
Solution:
Draw DQ ⊥ BC, B-C-Q.

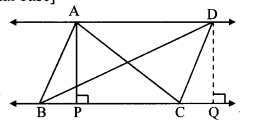
AD || BC [Given]
∴ AP = DQ   (i)  [Perpendicular distance between two parallel lines is the same]
∆ABC and ∆BCD have same base BC.

Question 5.
In the adjoining figure, PQ ⊥ BC, AD ⊥ BC, then find following ratios.

Solution:
i. ∆PQB and tPBC have same height PQ.

ii. ∆PBC and ∆ABC have same base BC.

iii. ∆ABC and ∆ADC have same height AD.

Question 1.
Find \(\frac{A(\Delta A B C)}{A(\Delta A P Q)}\)

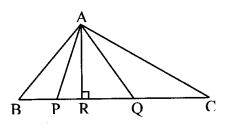
Solution:
In ∆ABC, BC is the base and AR is the height.
In ∆APQ, PQ is the base and AR is the height.