Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 4.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 4 Geometric Constructions.
10th Standard Maths 2 Practice Set 4.2 Chapter 4 Geometric Constructions Textbook Answers Maharashtra Board
Class 10 Maths Part 2 Practice Set 4.2 Chapter 1 Geometric Constructions Questions With Answers Maharashtra Board
Question 1.
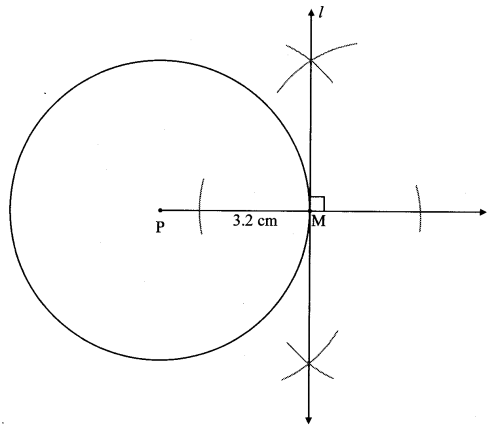
Construct a tangent to a circle with centre P and radius 3.2 cm at any point M on it.
Solution:
Analysis:
seg PM ⊥ line l ….[Tangent is perpendicular to radius]
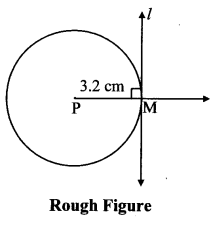
The perpendicular to seg PM at point M will give the required tangent at M.
Question 2.
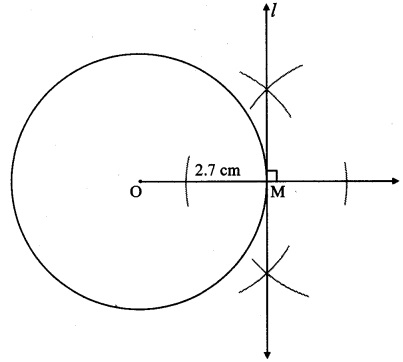
Draw a circle of radius 2.7 cm. Draw a tangent to the circle at any point on it.
Solution:
Analysis:
seg OM ⊥ line l …[Tangent is perpendicular to radius]
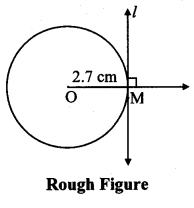
The perpendicular to seg OM at point M will give the required tangent at M.
Question 3.
Draw a circle of radius 3.6 cm. Draw a tangent to the circle at any point on it without using the centre.
Solution:
Analysis:
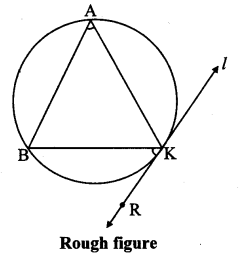
As shown in the figure, line lis a tangent to the circle at point K.
seg BK is a chord of the circle and LBAK is an inscribed angle.
By tangent secant angle theorem,
∠BAK = ∠BKR
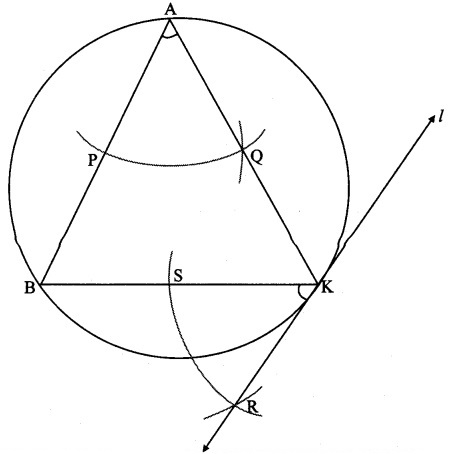
By converse of tangent secant angle theorem,
If we draw ∠BKR such that ∠BKR = ∠BAK, then ray KR
i.e. (line l) is a tangent at point K.
Question 4.
Draw a circle of radius 3.3 cm. Draw a chord PQ of length 6.6 cm. Draw tangents to the circle at points P and Q. Write your observation about the tangents.
Solution:
Analysis:
seg OP ⊥ line l …[Tangent is perpendicular to radius]
seg OQ ⊥ line m
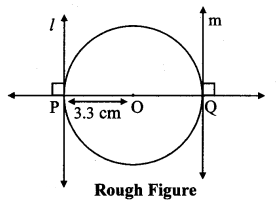
The perpendicular to seg OP and seg OQ at points P and Q
respectively will give the required tangents at P and Q.
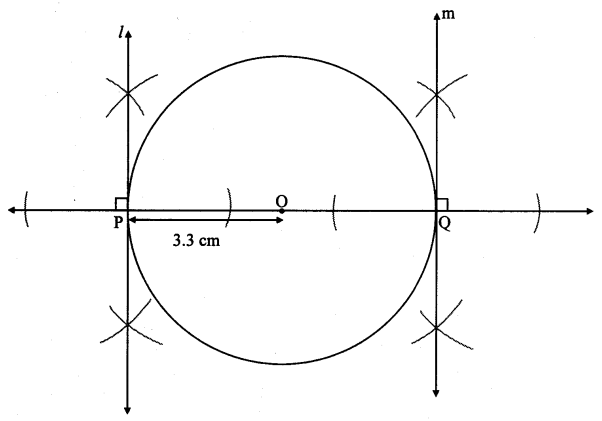
Radius = 3.3 cm
∴ Diameter = 2 × 3.3 = 6.6 cm
∴ Chord PQ is the diameter of the circle.
∴ The tangents through points P and Q (endpoints of diameter) are parallel to each other.
Question 5.
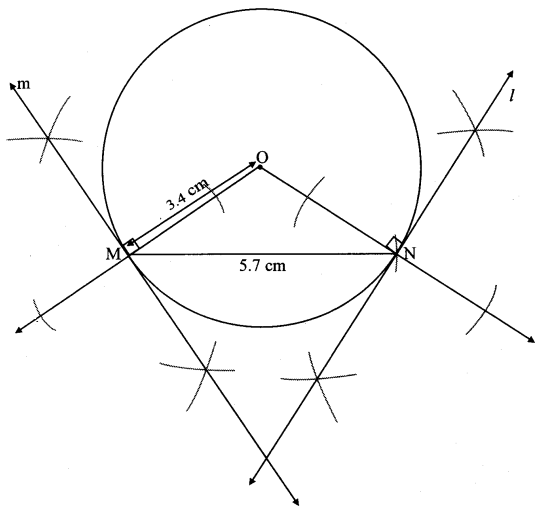
Draw a circle with radius 3.4 cm. Draw a chord MN of length 5.7 cm in it. Construct tangents at points M and N to the circle.
Solution:
Analysis:
seg ON ⊥ linel l
seg OM ⊥ Iine m …….[Tangent is perpendicular to radius]
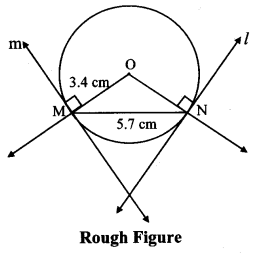
The perpendicular to seg ON and seg 0M at points N and M respectively will give the required tangents at N and M.
Question 6.
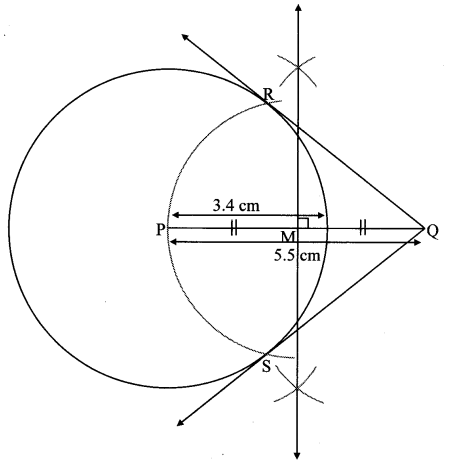
Draw a circle with centre P and radius 3.4 cm. Take point Q at a distance 5.5 cm from the centre. Construct tangents to the circle from point Q.
Solution:
Analysis:
As shown in the figure, let Q be a point in the exterior of circle at a distance of 5.5 cm.
Let QR and QS be the tangents to the circle at points R and S respectively.
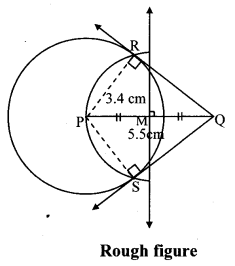
∴ seg PR ⊥ tangent QR …[Tangent is perpendicular to radius]
∴ ∠PRQ = 90°
∴ point R is on the circle having PQ as diameter. …[Angle inscribed in a semicircle is a right angle]
Similarly, point S also lies on the circle having PQ as diameter.
∴ Points R and S lie on the circle with PQ as diameter.
On drawing a circle with PQ as diameter, the points where it intersects the circle with centre P, will be the positions of points R and S respectively.
Ray QR and QS are the required tangents to the circle from point Q.
Question 7.
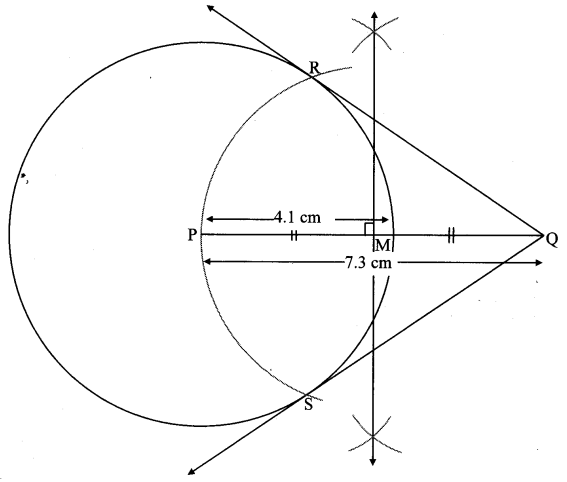
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Solution:
Analysis:
As shown in the figure, let Q be a point in the exterior of circle at a distance of 5.5 cm.
Let QR and QS be the tangents to the circle at points R and S respectively.
∴ seg PR ⊥ tangent QR …[Tangent is perpendicular to radius]
∴ ∠PRQ = 90°
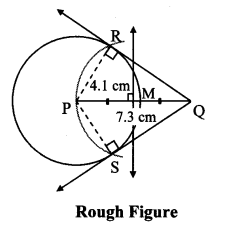
∴ point R is on the circle having PQ as diameter. …[Angle inscribed in a semicircle is a right angle]
Similarly, point S also lies on the circle having PQ as diameter.
∴ Points R and S lie on the circle with PQ as diameter.
On drawing a circle with PQ as diameter, the points where it intersects the circle with centre P, will be the positions of points R and S respectively.
Ray QR and QS are the required tangents to the circle from point Q.