Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.1 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 5 Co-ordinate Geometry.
10th Standard Maths 2 Practice Set 5.1 Chapter 5 Co-ordinate Geometry Textbook Answers Maharashtra Board
Class 10 Maths Part 2 Practice Set 5.1 Chapter 5 Co-ordinate Geometry Questions With Answers Maharashtra Board
Practice Set 5.1 Geometry Class 10 Question 1. Find the distance between each of the following pairs of points.
i. A (2, 3), B (4,1)
ii. P (-5, 7), Q (-1, 3)
iii. R (0, -3), S (0,\(\frac { 5 }{ 2 } \))
iv. L (5, -8), M (-7, -3)
v. T (-3, 6), R (9, -10)
vi. W(\(\frac { -7 }{ 2 } \),4), X(11, 4)
Solution:
i. Let A (x
1
, y
1
) and B (x
2
, y
2
) be the given points.
∴ x
1
= 2, y
1
= 3, x
2
= 4, y
2
= 1
By distance formula,
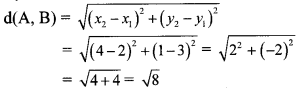
∴ d(A, B) = 2\(\sqrt { 2 }\) units
∴ The distance between the points A and B is 2\(\sqrt { 2 }\) units.
ii. Let P (x
1
, y
1
) and Q (x
2
, y
2
) be the given points.
∴ x
1
= -5, y
1
= 7, x
2
= -1, y
2
= 3
By distance formula,
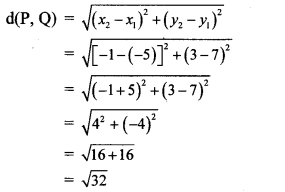
∴ d(P, Q) = 4\(\sqrt { 2 }\) units
∴ The distance between the points P and Q is 4\(\sqrt { 2 }\) units.
iii. Let R (x
1
, y
1
) and S (x
2
, y
2
) be the given points.
∴ x
1
= 0, y
1
= -3, x
2
= 0, y
2
= \(\frac { 5 }{ 2 } \)
By distance formula,

∴ d(R, S) = \(\frac { 11 }{ 2 } \) units
∴ The distance between the points R and S is \(\frac { 11 }{ 2 } \) units.
iv. Let L (x
1
, y
1
) and M (x
2
, y
2
) be the given points.
∴ x
1
= 5, y
1
= -8, x
2
= -7, y
2
= -3
By distance formula,
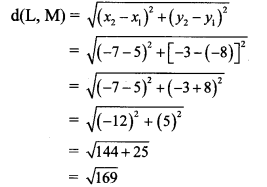
∴ d(L, M) = 13 units
∴ The distance between the points L and M is 13 units.
v. Let T (x
1
,y
1
) and R (x
2
, y
2
) be the given points.
∴ x
1
= -3, y
1
= 6,x
2
= 9,y
2
= -10
By distance formula,
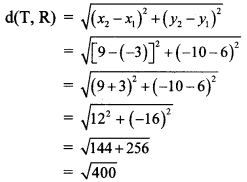
∴ d(T, R) = 20 units
∴ The distance between the points T and R 20 units.
vi. Let W (x
1
, y
1
) and X (x
2
, y
2
) be the given points.

∴ d(W, X) = \(\frac { 29 }{ 2 } \) units
∴ The distance between the points W and X is \(\frac { 29 }{ 2 } \) units.
Practice Set 5.1 Geometry 10th Question 2. Determine whether the points are collinear.
i. A (1, -3), B (2, -5), C (-4, 7)
ii. L (-2, 3), M (1, -3), N (5, 4)
iii. R (0, 3), D (2, 1), S (3, -1)
iv. P (-2, 3), Q (1, 2), R (4, 1)
Solution:
i. By distance formula,
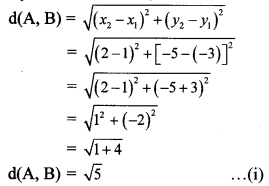
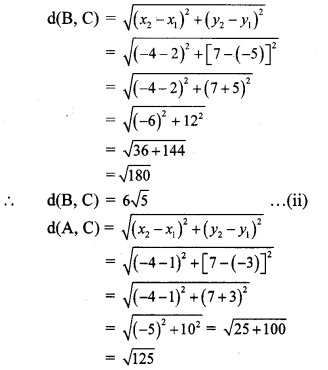
∴ d(A, B) = \(\sqrt { 5 }\) …(i)
On adding (i) and (iii),
d(A, B) + d(A, C)= \(\sqrt { 5 }\) + 5\(\sqrt { 5 }\) = 6\(\sqrt { 5 }\)
∴ d(A, B) + d(A, C) = d(B, C) … [From (ii)]
∴ Points A, B and C are collinear.
ii. By distance formula,
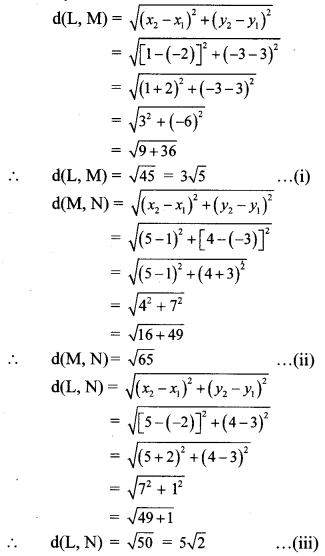
On adding (i) and (iii),
d(L, M) + d(L, N) = 3\(\sqrt { 5 }\) + 5\(\sqrt { 2 }\) ≠ \(\sqrt { 65 }\)
∴ d(L, M) + d(L, N) ≠ d(M, N) … [From (ii)]
∴ Points L, M and N are not collinear.
iii. By distance formula,
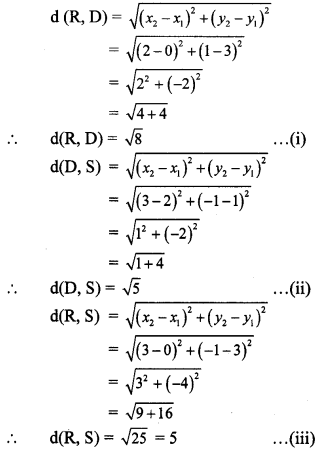
On adding (i) and (ii),
∴ d(R, D) + d(D, S) = \(\sqrt { 8 }\) + \(\sqrt { 5 }\) ≠ 5
∴ d(R, D) + d(D, S) ≠ d(R, S) … [From (iii)]
∴ Points R, D and S are not collinear.
iv. By distance formula,
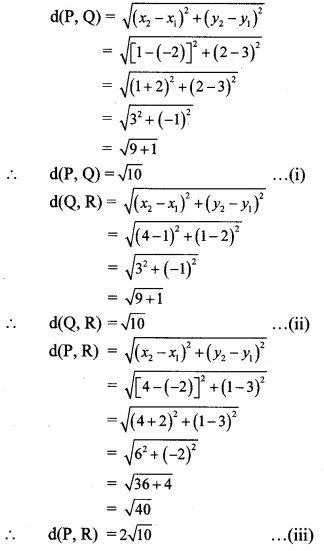
On adding (i) and (ii),
d(P, Q) + d(Q, R) = \(\sqrt { 10 }\) + \(\sqrt { 10 }\) = 2\(\sqrt { 10 }\)
∴ d(P, Q) + d(Q, R) = d(P, R) … [From (iii)]
∴ Points P, Q and R are collinear.
Coordinate Geometry Class 10 Practice Set 5.1 Question 3. Find the point on the X-axis which is equidistant from A (-3,4) and B (1, -4).
Solution:
Let point C be on the X-axis which is equidistant from points A and B.
Point C lies on X-axis.
∴ its y co-ordinate is 0.
Let C = (x, 0)
C is equidistant from points A and B.
∴ AC = BC
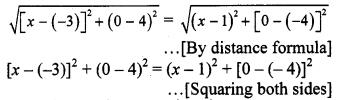
∴ (x + 3)
2
+ (-4)
2
= (x- 1)
2
+ 4
2
∴ x
2
+ 6x + 9 + 16 = x
2
– 2x + 1 + 16
∴ 8x = – 8
∴ x = – \(\frac { 8 }{ 8 } \) = -1
∴ The point on X-axis which is equidistant from points A and B is (-1,0).
10th Geometry Practice Set 5.1 Question 4. Verify that points P (-2, 2), Q (2, 2) and R (2, 7) are vertices of a right angled triangle.
Solution:
Distance between two points

Consider, PQ
2
+ QR
2
= 42 + 52 = 16 + 25 = 41 … [From (i) and (ii)]
∴ PR
2
= PQ
2
+ QR
2
… [From (iii)]
∴ ∆PQR is a right angled triangle. … [Converse of Pythagoras theorem]
∴ Points P, Q and R are the vertices of a right angled triangle.
Question 5.
Show that points P (2, -2), Q (7, 3), R (11, -1) and S (6, -6) are vertices of a parallelogram.
Proof:
Distance between two points

PQ = RS … [From (i) and (iii)]
QR = PS … [From (ii) and (iv)]
A quadrilateral is a parallelogram, if both the pairs of its opposite sides are congruent.
∴ □ PQRS is a parallelogram.
∴ Points P, Q, R and S are the vertices of a parallelogram.
Question 6.
Show that points A (-4, -7), B (-1, 2), C (8, 5) and D (5, -4) are vertices of rhombus ABCD.
Proof:
Distance between two points

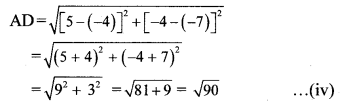
∴ AB = BC = CD = AD …[From (i), (ii), (iii) and (iv)]
In a quadrilateral, if all the sides are equal, then it is a rhombus.
∴ □ ABCD is a rhombus.
∴ Points A, B, C and D are the vertices of rhombus ABCD.
Practice Set 5.1 Question 7. Find x if distance between points L (x, 7) and M (1,15) is 10.
Solution:
X
1
= x, y
1
= 7, x
2
= 1, y
2
= 15
By distance formula,

∴ 1 – x = ± 6
∴ 1 – x = 6 or l – x = -6
∴ x = – 5 or x = 7
∴ The value of x is – 5 or 7.
Geometry 5.1 Question 8. Show that the points A (1, 2), B (1, 6), C (1 + 2\(\sqrt { 3 }\), 4) are vertices of an equilateral triangle.
Proof:
Distance between two points

∴ AB = BC = AC … [From (i), (ii) and (iii)]
∴ ∆ABC is an equilateral triangle.
∴ Points A, B and C are the vertices of an equilateral triangle.
Maharashtra Board Class 10 Maths Chapter 5 Coordinate Geometry Intext Questions and Activities
Question 1.
In the figure, seg AB || Y-axis and seg CB || X-axis. Co-ordinates of points A and C are given. To find AC, fill in the boxes given below. (Textbook pa. no. 102)
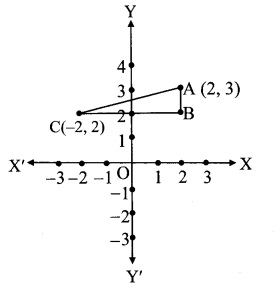
Solution:
In ∆ABC, ∠B = 900
∴ (AB)
2
+ (BC)
2
= [(Ac)
2
…(i) … [Pythagoras theorem]
seg CB || X-axis
∴ y co-ordinate of B = 2
seg BA || Y-axis
∴ x co-ordinate of B = 2
∴ co-ordinate of B is (2, 2) = (x
1
,y
1
)
co-ordinate of A is (2, 3) = (x
2
, Y
2
)
Since, AB || to Y-axis,
d(A, B) = Y
2
– Y
1
d(A,B) = 3 – 2 = 1
co-ordinate of C is (-2,2) = (x
1
,y
1
)
co-ordinate of B is (2, 2) = (x
2
, y
2
)
Since, BC || to X-axis,
d(B, C) = x
2
– x
1
d(B,C) = 2 – -2 = 4
∴ AC
2
= 12 + 42 …[From (i)]
= 1 + 16 = 17
∴ AC = \(\sqrt { 17 }\) units …[Taking square root of both sides]