Problem Set 6 Geometry 10th Standard Maths Part 2 Chapter 6 Trigonometry Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 6 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 6 Trigonometry.

10th Standard Maths 2 Problem Set 6 Chapter 6 Trigonometry Textbook Answers Maharashtra Board

Class 10 Maths Part 2 Problem Set 6 Chapter 6 Trigonometry Questions With Answers Maharashtra Board

Question 1.
Choose the correct alternative answer for the following questions.

i. sin θ.cosec θ = ?
(A) 1
(B) 0
(C) \(\frac { 1 }{ 2 } \)
(D) \(\sqrt { 2 }\)
Answer:
(A)

ii. cosec 45° = ?
(A) \(\frac{1}{\sqrt{2}}\)
(B) \(\sqrt { 2 }\)
(C) \(\frac{\sqrt{3}}{2}\)
(D) \(\frac{1}{\sqrt{3}}\)
Answer:
(B)

iii. 1 + tan ² θ = ?
(A) cot ² θ
(B) cosec ² θ
(C) sec ² θ
(D) tan ² θ
Answer:
(C)

iv. When we see at a higher level, from the horizontal line, angle formed is ______
(A) angle of elevation.
(B) angle of depression.
(C) 0
(D) straight angle.
Answer:
(A)

Question 2.
If sin θ = \(\frac { 11 }{ 61 } \), find the value of cos θ using trigonometric identity.
Solution:
sin θ = \(\frac { 11 }{ 61 } \) … [Given]
We know that,
sin ² θ + cos ² θ = 1


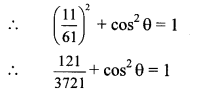
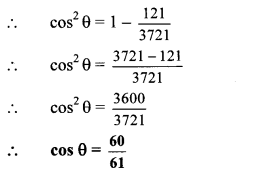
…[Taking square root of both sides]

Question 3.
If tan θ = 2, find the values of other trigonometric ratios.
Solution:
tan θ = 2 …[Given]
We know that,
1 + tan ² θ = sec ⁷ θ
∴ 1 + (2) ⁷ = sec ⁷ θ
∴ 1 + 4 = sec ⁷ θ
∴ sec ⁷ θ = 5
∴ sec θ = \(\sqrt { 5 }\) …[Taking square root of both sides]

Question 4.
If sec θ = \(\frac { 13 }{ 12 } \), find the values of other trigonometric ratios.
Solution:
sec θ = \(\frac { 13 }{ 12 } \) … [Given]
We know that,
1 + tan ² θ = sec ² θ


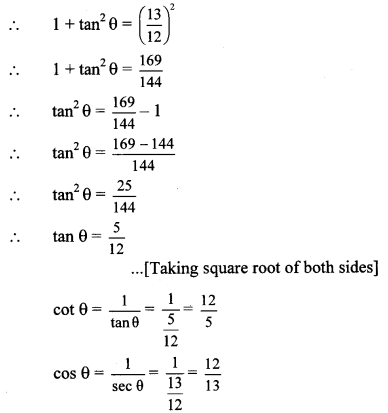
∴ sin θ = \(\frac { 5 }{ 13 } \), cos θ = \(\frac { 12 }{ 13 } \), tan θ = \(\frac { 5 }{ 12 } \), cot θ = \(\frac { 12 }{ 5 } \), cosec θ = \(\frac { 13 }{ 5 } \)

Question 5.
Prove the following:
i. sec θ (1 – sin θ) (sec θ + tan θ) = 1
ii. (sec θ + tan θ) (1 – sin θ) = cos θ
iii. sec ² θ + cosec ² θ = sec ² θ × cosec ² θ
iv. cot ² θ – tan ² θ = cosec ² θ – sec ² θ
v. tan ⁴ θ + tan ² θ = sec ⁴ θ – sec ² θ
vi. \(\frac{1}{1-\sin \theta}+\frac{1}{1+\sin \theta}\) = 2 sec2 θ
vii. sec ⁶ x – tan ⁶ x = 1 + 3 sec ² x × tan ² x

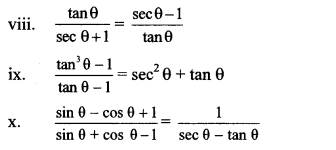
Proof:
i. L.H.S. = sec θ (1 – sin θ) (sec θ + tan θ)

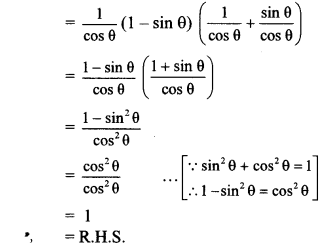
∴ sec θ (1 – sin θ) (sec θ + tan θ) = 1

ii. L.H.S. = (sec θ + tan θ) (1 – sin θ)

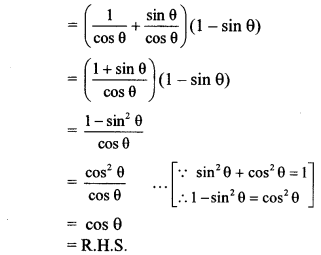
∴ (sec θ + tan θ) (1 – sin θ) = cos θ

iii. L.H.S. = sec ² θ + cosec ² θ

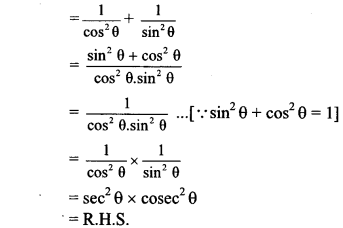
∴ sec ² θ + cosec ² θ = sec ² θ × cosec ² θ

iv. L.H.S. = cot ² θ – tan ² θ
= (cosec ² θ – 1) – (sec ² θ – 1)
[∵ tan ² θ = sec ² θ – 1,
cot ² θ = cosec ² θ – 1]
= cosec ² θ – 1 – sec ² θ + 1
cosec ² θ – sec ² θ
= R.H.S.
∴ cot ² θ – tan ² θ = cosec ² θ – sec ² θ

v. L.H.S. = tan ⁴ θ + tan ² θ
= tan ² θ (tan ² θ + 1)
= tan ² θ. sec ² θ
…[∵ 1 + tan ² θ = sec ² θ]
= (sec ² θ – 1) sec ² θ
…[∵ tan ² θ = sec ² θ – 1]
= sec ⁴ θ – sec ² θ
= R.H.S.
∴ tan ⁴ θ + tan ² θ = sec ⁴ θ – sec ² θ

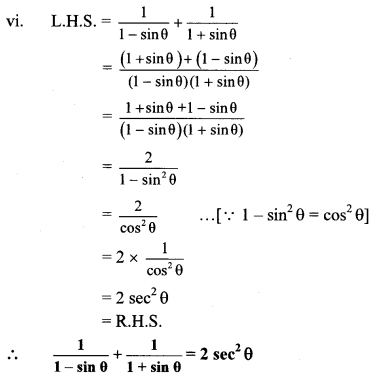
vii. L.H.S. = sec ⁶ x – tan ⁶ x
= (sec ² x) ³ – tan ⁶ x
= (1 + tan ² x) ³ – tan ⁶ x …[∵ 1 + tan ² θ = sec ² θ]
= 1 + 3tan ² x + 3(tan ² x) ² + (tan ² x) ³ – tan ⁶ x …[∵ (a + b) ³ = a ³ + 3a ² b + 3ab ² + b ³ ]
= 1 + 3 tan ² x (1 + tan ² x) + tan ⁶ x – tan ⁶ x
= 1 + 3 tan ² x sec ² x …[∵ 1 + tan ² θ = sec ² θ]
= R.H.S.
∴ sec ³ x – tan ⁶ x = 1 + 3sec ² x.tan ² x


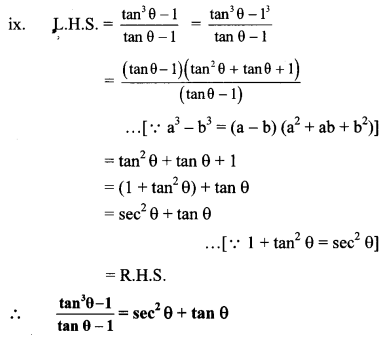
x. We know that,
sin ² θ + cos ² θ = 1
∴ 1 – sin ² θ = cos ² θ
∴ (1 – sin θ) (1 + sin θ) = cos θ. cos θ

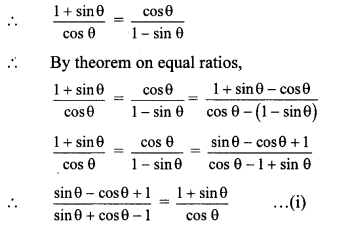
Question 6.
A boy standing at a distance of 48 metres from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
Solution:
Let AB represent the height of the building and point C represent the position of the boy.
Angle of elevation = ∠ACB = 30°
BC = 48 m

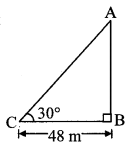
In right angled ∆ABC,
tan 30° = \(\frac { AB }{ BC } \) … [By definition]

∴ The height of the building is 16\(\sqrt { 3 }\) m.

Question 7.
From the top of the lighthouse, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the lighthouse is 100 metres, then find how far the ship is from the lighthouse.
Solution:
Let AB represent the height of lighthouse and point C represent the position of the ship.

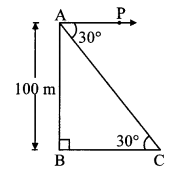
Angle of depression ∠PAC 30°
AB = 100m.
Now, ray AP || seg BC
∴ ∠ACB = ∠PAC … [Alternate angles]
∴ ∠ACB = 30°
AB = 100m
In right angled ∆ABC,
tan 30° = \(\frac { AB }{ BC } \) …[By definition]
∴ \(\frac{1}{\sqrt{3}}=\frac{100}{\mathrm{BC}}\)
∴ BC = 100\(\sqrt { 3 }\)m
∴ The ship is 1oo\(\sqrt { 3 }\)m far from the lighthouse.

Question 8.
Two buildings are in front of each other on a road of width 15 metres. From the top of the first building, having a height of 12 metre, the angle of elevation of the top of the second building is 30°. What is the height of the second building?
Solution:
Let AB and CD represent the heights of the two buildings, and BD represent the width of the road.

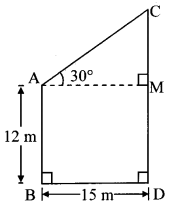
Draw seg AM ⊥ seg CD
Angle of elevation = ∠CAM = 30°
AB = 12m
BD = 15m
In ꠸ ABDM,
∠B = ∠D = 90°
∠M 90° …[segAM ⊥ segCD]
∠A 90° …[Remaining angle of ꠸ABDM]
꠸ABDM is a rectangle …[Each angle is 90°]

∴ The height of the second building is 20.65 m.

Question 9.
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2 m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
Solution:
Let AB represent the length of the ladder and AE represent the height of the platform.

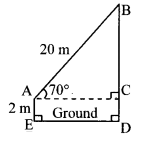
Draw seg AC ⊥ seg BD.
Angle of elevation = ∠BAC = 70°
AB = 20 m
AE = 2m
In right angled ∆ABC,
sin 70° = \(\frac { BC }{ AB } \) …..[By definition]
∴ 0.94 = \(\frac { BC }{ 20 } \)
∴ BC = 0.94 × 20
= 18.80 m
In ꠸ACDE,
∠E = ∠D = 90°
∠C = 90° … [seg AC ⊥ seg BD]
∴ ∠A = 90° … [Remaining angle of ꠸ACDE]
∴ ꠸ACDE is a rectangle. … [Each angle is 90°]
∴ CD = AE = 2 m … [Opposite sides of a rectangle]
Now, BD = BC + CD … [B – C – D]
= 18.80 + 2
= 20.80 m
∴ The maximum height from the ground upto which the ladder can reach is 20.80 metres.

Question 10.
While landing at an airport, a pilot made an angle of depression of 20°. Average speed of the plane was 200 km/hr. The plane reached the ground after 54 seconds. Find the height at which the plane was when it started landing, (sin 20° = 0.342)
Solution:
Let AC represent the initial height and point A represent the initial position of the plane.
Let point B represent the position where plane lands.
Angle of depression = ∠EAB = 20°

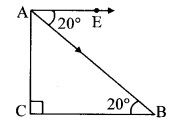
Now, seg AE || seg BC
∴ ∠ABC = ∠EAB … [Alternate angles]
∴ ∠ABC = 20°
Speed of the plane = 200 km/hr
= 200 × \(\frac { 1000 }{ 3600 } \) m/sec
= \(\frac { 500 }{ 9 } \) m/sec
∴ Distance travelled in 54 sec = speed × time
= \(\frac { 500 }{ 9 } \) × 54
= 3000 m
∴ AB = 3000 m
In right angled ∆ABC,
sin 20° = \(\frac { AC }{ AB } \) ….[By definition]
∴ 0.342 = \(\frac { AC }{ 3000 } \)
∴ AC = 0.342 × 3000
= 1026 m
∴ The plane was at a height of 1026 m when it started landing.