Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 2.2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 2 Real Numbers.
9th Standard Maths 1 Practice Set 2.2 Chapter 2 Real Numbers Textbook Answers Maharashtra Board
Class 9 Maths Part 1 Practice Set 2.2 Chapter 2 Real Numbers Questions With Answers Maharashtra Board
Question 1.
Show that 4√2 is an irrational number.
Solution:
Let us assume that 4√2 is a rational number .
So, we can find co-prime integers ‘a’ and ‘b’ (b ≠ 0) such that
4√2 = \(\frac { a }{ b }\)
∴ √2 = \(\frac { a }{ 4b }\)
Since, a and b are integers, \(\frac { a }{ 4b }\) is a rational number and so √2 is a rational number.
Alternate Proof:
Let us assume that 4√2 is a rational number.
So, we can find co-prime integers ‘a’ and ‘b’ (b ≠ 0) such that

Since, 32 divides a
2
, so 32 divides ‘a’ as well.
So, we write a = 32c, where c is an integer.
∴ a
2
= (32c)
2
… [Squaring both the sides]
∴ 32b
2
= 32 x 32c
2
…[From(i)]
∴ b
2
= 32c
2
∴ c
2
= \(\frac { { b }^{ 2 } }{ 32 }\)
Since, 32 divides b
2
, so 32 divides ‘b’.
∴ 32 divides both a and b.
a and b have at least 32 as a common factor.
But this contradicts the fact that a and b have no common factor other than 1.
∴ Our assumption that 4√2 is a rational number is wrong.
∴ 4√2 is an irrational number.
Question 2.
Prove that 3 + √5 is an irrational number.
Solution:
Let us assume that 3 + √5 is a rational number.
So, we can find co-prime integers ‘a’ and ‘b’ (b ≠ 0) such that
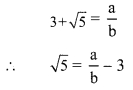
Since, a and b are integers, \(\frac { a }{ b }\) – 3 is a rational
number and so √5 is a rational number.
But this contradicts the fact that √5 is an irrational number.
∴ Our assumption that 3 – √5 is a rational number is wrong.
3 + √5 is an irrational number.
Question 3.
Represent the numbers √5 and √10 on a number line.
Solution:
i. Draw a number line and take point A at 2.
Draw AB perpendicular to the number line such that AB = 1 unit.
In ∆OAB, m∠OAB = 90°
∴ (OB)
2
= (OA)
2
+ (AB)
2
… [Pythagoras theorem]
= (2)
2
+ (1)
2
∴ (OB)
2
= 5
∴ OB = √5 units. … [Taking square root of both sides]
With O as centre and radius equal to OB, draw an arc to intersect the number line at C.
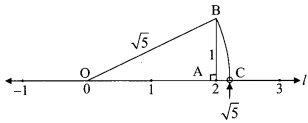
The coordinate of the point C is √5 .
ii. Draw a number line and take point Pat 3.
Draw PR perpendicular to the number line such that PR = 1 unit.
In ∆OPR, m∠OPR = 90°
∴ (OR)
2
= (OP)
2
+ (PR)
2
… [Pythagoras theorem]
= (3)
2
+ (1)
2
∴ (OR)
2
= 10
∴ OR= √10units. … [Taking square root of both sides]
With O as centre and radius equal to OR, draw an arc to intersect the number line at Q.
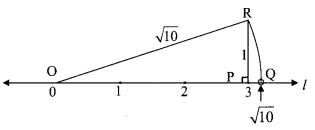
The coordinate of the point Q is √10 .
Question 4.
Write any three rational numbers between the two numbers given below.
i. 0.3 and – 0.5
ii. – 2.3 and – 2.33
iii. 5.2 and 5.3
iv. – 4.5 and – 4.6
Solution:
i. 0.3 = 0.30 and -0.5 = -0.50
We know that,
0. 30 >0.29 >….. >0.10>.. > – 0.10>…. > -0.30>…> -0.50
∴ the three rational numbers between 0.3 and -0.5 are -0.3, -0.1 and 0.1.
Alternate Method:
A rational number between two rational numbers a and b
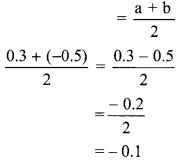
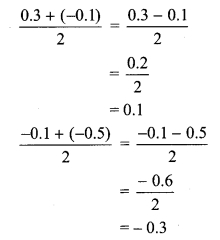
∴ the three rational numbers between 0.3 and -0.5 are -0.3, -0.1 and 0.1.
ii. -2.3 = -2.300 and -2.33 = -2.330
We know that,
-2.300 > -2.301>… > -2.310>…> -2.320>…> -2.330
∴ the three rational numbers between -2.3 and -2.33 are -2.310, -2.320 and -2.325.
iii. 5.2 = 5.20 and 5.3 = 5.30
We know that,
5.20 < 5.21 < 5.22 < 5.23 < … < 5.30
∴ the three rational numbers between 5.2 and 5.3 are 5.21, 5.22 and 5.23.
iv. -4.5 = -4.50 and -4.6 = -4.60 We know that,
-4.50 > -4.51 > -4.52 >… > – 4.55 >…>- 4.60
∴ the three rational numbers between -4.5 and -4.6 are -4.51, -4.52 and -4.55.