Practice Set 3.2 Algebra 9th Standard Maths Part 1 Chapter 3 Polynomials Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 3.2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 3 Polynomials.

9th Standard Maths 1 Practice Set 3.2 Chapter 3 Polynomials Textbook Answers Maharashtra Board

Class 9 Maths Part 1 Practice Set 3.2 Chapter 3 Polynomials Questions With Answers Maharashtra Board

Question 1.
Use the given letters to write the answer.
i. There are ‘a’ trees in the village Lat. If the number of trees increases every year by ’b‘. then how many trees will there be after ‘x’ years?
ii. For the parade there are y students in each row and x such row are formed. Then, how many students are there for the parade in all ?
iii. The tens and units place of a two digit number is m and n respectively. Write the polynomial which represents the two digit number.
Solution:
i. Number of trees in the village Lat = a
Number of trees increasing each year = b
∴ Number of trees after x years = a + bx
∴ There will be a + bx trees in the village Lat after x years.

ii. Total rows = x
Number of students in each row = y
∴ Total students = Total rows × Number of students in each row
= x × y
= xy
∴ There are in all xy students for the parade.

iii. Digit in units place = n
Digit in tens place = m
∴ The two digit number = 10 x digit in tens place + digit in units place
= 10m + n
∴ The polynomial representing the two digit number is 10m + n.

Question 2.
Add the given polynomials.
i. x ³ – 2x ² – 9; 5x ³ + 2x + 9
ii. -7m ⁴ + 5m ³ + √2 ; 5m ⁴ – 3m ³ + 2m ² + 3m – 6
iii. 2y ² + 7y + 5; 3y + 9; 3y ² – 4y – 3
Solution:
i. (x ³ – 2x ² – 9) + (5x ³ + 2x + 9)
= x ³ – 2x ² – 9 + 5x ³ + 2x + 9
= x ³ + 5x ³ – 2x ² + 2x – 9 + 9
= 6x ³ – 2x ² + 2x

ii. (-7m ⁴ + 5m ³ + √2 ) + (5m ⁴ – 3m ³ + 2m ² + 3m – 6)
= -7m ⁴ + 5m ³ + √2 + 5m ⁴ – 3m ³ + 2m ² + 3m – 6
= -7m ⁴ + 5m ⁴ + 5m ³ – 3m ³ + 2m ² + 3m + √2 – 6
= -2m ⁴ + 2m ³ + 2m ² + 3m + √2 – 6

iii. (2y ² + 7y + 5) + (3y + 9) + (3y ² – 4y – 3)
= 2y ² + 7y + 5 + 3y + 9 + 3y ² – 4y – 3
= 2y ² + 3y ² + 7y + 3y – 4y + 5 + 9 – 3
= 5y ² + 6y + 11

Question 3.
Subtract the second polynomial from the first.
i. x ² – 9x + √3 ; – 19x + √3 + 7x ²
ii. 2ab ² + 3a ² b – 4ab; 3ab – 8ab ² + 2a ² b
Solution:
i. x ² – 9x + √3 -(- 19x + √3 + 7x ² )
= x ² – 9x + √3 + 19x – √ 3 – 7x ²
= x ² – 7x ² – 9x + 19x + √3 – √3
= – 6x ² + 10x

ii. (2ab ² + 3a ² b – 4ab) – (3ab – 8ab ² + 2a ² b)
= 2ab ² + 3a ² b – 4ab – 3ab + 8ab ² – 2a ² b
= 2ab ² + 8ab ² + 3a ² b – 2a ² b – 4ab – 3ab
= 10ab ² + a ² b – 7ab

Question 4.
Multiply the given polynomials.
i. 2x; x ² – 2x – 1
ii. x ⁵ – 1; x ³ + 2x ² + 2
iii. 2y +1; y ² – 2y + 3y
Solution:
i. (2x) x (x ² – 2x – 1) = 2x ³ – 4x ² – 2x

ii. (x ⁵ – 1) × (x ³ + 2x ² + 2)
= x ⁵ (x ³ + 2x ² + 2) -1(x ³ + 2x ² + 2)
= x ⁸ + 2x ⁷ + 2x ⁵ – x ³ – 2x ² – 2

iii. (2y + 1) × (y ² – 2y ³ + 3y)
= 2y(y ² – 2y ³ + 3y) + 1(y ² – 2y ³ + 3y)
= 2y ³ – 4y ⁴ + 6y ² + y ² – 2y ³ + 3y
= -4y ⁴ + 2y ³ – 2y ³ + 6y ² + y ² + 3y
= -4y ⁴ + 7y ² + 3y

Question 5.
Divide first polynomial by second polynomial and write the answer in the form ‘Dividend = Divisor x Quotient + Remainder’.
i. x ³ – 64; x – 4
ii. 5x ⁵ + 4x ⁴ – 3x ³ + 2x ² + 2 ; x ² – x
Solution:
i. x ³ – 64 = x3 + 0x ² + 0x – 64

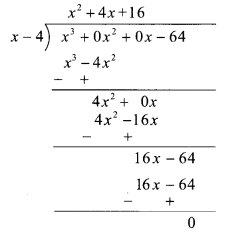
∴ Quotient = x ² + 4x + 16, Remainder = 0
Now, Dividend = Divisor x Quotient + Remainder
∴ x ³ – 64 = (x – 4)(x ² + 4x + 16) + 0

ii. 5x ⁵ + 4x ⁴ – 3x ³ + 2x ² + 2 = 5x ⁵ + 4x ⁴ – 3x ³ + 2x + 0x + 2

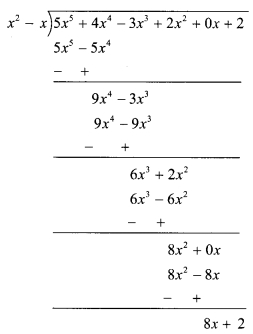
∴ Quotient = 5x ³ + 9x ² + 6x + 8,
Remainder = 8x + 2
Now, Dividend = Divisor x Quotient + Remainder
∴ 5x ⁵ + 4x ⁴ – 3x ³ + 2x ² + 2 = (x ² – x)(5x ³ + 9x ² + 6x + 8) + (8x + 2)

Question 6.
Write down the information in the form of algebraic expression and simplify.
There is a rectangular farm with length (2a ² + 3b ² ) metre and breadth (a ² + b ² ) metre. The farmer used a square shaped plot of the farm to build a house. The side of the plot was (a2 – b2) metre. What is the area of the remaining part of the farm? [4 Marks]
Solution:
Length of the rectangular farm = (2a ² + 3b ² ) m
Breadth of the rectangular farm = (a ² + b ² ) m
Area of the farm = length x breadth = (2a ² + 3b ² ) x (a ² + b ² )
= 2a ² (a ² + b ² ) + 3b ² (a ² + b ² )
= 2a ² + 2a ² b ² + 3a ² b ² + 3b ⁴
= (2a ⁴ + 5a ² b ² + 3b ⁴ ) sq. m … (i)
The farmer used a square shaped plot of the farm to build a house.
Side of the square shaped plot = (a ² – b ² ) m
∴ Area of the plot = (side) ²
= (a ² – b ² ) ²
= (a ⁴ – 2a ² b ² + b ⁴ ) sq m… .(ii)

∴ Area of the remaining farm = Area of the farm – Area of the plot
= (2a ⁴ + 5a ² b ² + 3b ⁴ ) – (a ⁴ – 2a ² b ² + b ⁴ ) … [From (i) and (ii)]
= 2a ⁴ + 5a ² b ² + 3b ⁴ – a ⁴ + 2a ² b ² – b ⁴
= 2a ⁴ – a ⁴ + 5a ² b ² + 2a ² b ² + 3b ⁴ – b ⁴
= a ⁴ + 7a ² b ² + 2b ⁴
∴ The area of the remaining farm is (a ⁴ + 7a ² b ² + 2b ⁴ ) sq. m.