Practice Set 3.3 Algebra 9th Standard Maths Part 1 Chapter 3 Polynomials Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 3.3 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 3 Polynomials.

9th Standard Maths 1 Practice Set 3.3 Chapter 3 Polynomials Textbook Answers Maharashtra Board

Class 9 Maths Part 1 Practice Set 3.3 Chapter 3 Polynomials Questions With Answers Maharashtra Board

Question 1.
Divide each of the following polynomials by synthetic division method and also by linear division method. Write the quotient and the remainder.
i. (2m ² – 3m + 10) ÷ (m – 5)
ii. (x ⁴ + 2x ³ + 3x ² + 4x + 5) ÷ (x + 2)
iii. (y ³ – 216) ÷ (y – 6)
iv. (2x ⁴ + 3x ³ + 4x – 2x ² ) ÷ (x + 3)
v. (x ⁴ – 3x ² – 8) ÷ (x + 4)
vi. (y ³ – 3y ² + 5y – 1) ÷ (y – 1)
Solution:
i. Synthetic division:
(2m ² – 3m + 10) ÷ (m – 5)
Dividend = 2m² – 3m + 10
∴ Coefficient form of dividend = (2, -3, 10)
Divisor = m – 5
∴ Opposite of -5 is 5.

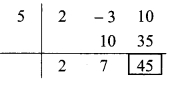
Coefficient form of quotient = (2, 7)
∴ Quotient = 2m + 7,
Remainder = 45
Linear division method:
2m ² – 3m + 10
To get the term 2m ² , multiply (m – 5) by 2m and add 10m,
= 2m(m – 5) + 10m- 3m + 10
= 2m(m – 5) + 7m + 10
To get the term 7m, multiply (m – 5) by 7 and add 35
= 2m(m – 5) + 7(m- 5) + 35+ 10
= (m – 5) (2m + 7) + 45
∴ Quotient = 2m + 7,
Remainder = 45

ii. Synthetic division:
(x ⁴ + 2x ³ + 3x ² + 4x + 5) ÷ (x + 2)
Dividend = x ⁴ + 2x ³ + 3x ² + 4x + 5
∴ Coefficient form of dividend = (1, 2, 3, 4, 5)
Divisor = x + 2
∴ Opposite of + 2 is -2.

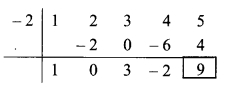
Coefficient form of quotient = (1, 0, 3, -2)
∴ Quotient = x ³ + 3x – 2,
Remainder = 9

Linear division method:
x ⁴ + 2x ³ + 3x ² + 4x + 5
To get the term x ⁴ , multiply (x + 2) by x ³ and subtract 2x ³ ,
= x ³ (x + 2) – 2x ³ + 2x ³ + 3x ² + 4x + 5
= x ³ (x + 2) + 3x ² + 4x + 5
To get the term 3x ² , multiply (x + 2) by 3x and subtract 6x,
= x ³ (x + 2) + 3x(x + 2) – 6x + 4x + 5
= x ³ (x + 2) + 3x(x + 2) – 2x + 5
To get the term -2x, multiply (x + 2) by -2 and add 4,
= x ³ (x + 2) + 3x(x + 2) – 2(x + 2) + 4 + 5
= (x + 2) (x3 + 3x – 2) + 9
∴ Quotient = x ³ + 3x – 2,
Remainder – 9

iii. Synthetic division:
(y ³ – 216) ÷ (y – 6)
Dividend = y ³ – 216
∴ Index form = y ³ + 0y ³ + 0y – 216
∴ Coefficient form of dividend = (1, 0, 0, -216)
Divisor = y – 6
∴ Opposite of – 6 is 6.

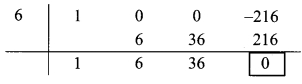
Coefficient form of quotient = (1, 6, 36)
∴ Quotient = y ² + 6y + 36,
Remainder = 0

Linear division method:
y ³ – 216
To get the term y ³ , multiply (y – 6) by y ² and add 6y ² ,
= y ² (y – 6) + 6y ² – 216
= y ² (y – 6) + 6ysup>2 – 216
To get the, term 6 y ² multiply (y – 6) by 6y and add 36y,
= y ² (y – 6) + 6y(y – 6) + 36y – 216
= y ² (y – 6) + 6y(y – 6) + 36y – 216
To get the term 36y, multiply (y- 6) by 36 and add 216,
= y ² (y – 6) + 6y(y – 6) + 36(y – 6) + 216 – 216
= (y – 6) (y ² + 6y + 36) + 0
Quotient = y ² + 6y + 36
Remainder = 0

iv. Synthetic division:
(2x ⁴ + 3x ³ + 4x – 2x ² ) ÷ (x + 3)
Dividend = 2x ⁴ + 3x ³ + 4x – 2x ²
∴ Index form = 2x ⁴ + 3x ³ – 2x ² + 4x + 0
∴ Coefficient form of the dividend = (2,3, -2,4,0)
Divisor = x + 3
∴ Opposite of + 3 is -3

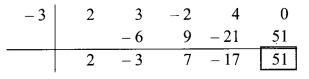
Coefficient form of quotient = (2, -3, 7, -17)
∴ Quotient = 2x ³ – 3x ² + 7x – 17,
Remainder = 51

Linear division method:
2x ⁴ + 3x ³ + 4x – 2x ² = 2x ² + 3x ³ – 2x ² + 4x
To get the term 2x ⁴ , multiply (x + 3) by 2x ³ and subtract 6x ³ ,
= 2x ³ (x + 31 – 6x ³ + 3x ³ – 2x ² + 4x
= 2x ³ (x + 3) – 3x ³ – 2x ² + 4x

To get the term – 3x ³ , multiply (x + 3) by -3x ² and add 9x ² ,
= 2x ³ (x + 3) – 3x ² (x + 3) + 9x ² – 2x ² + 4x
= 2x ³ (x + 3) – 3x ² (x + 3) + 7x ² + 4x

To get the term 7x ² , multiply (x + 3) by 7x and subtract 21x,
= 2x ³ (x + 3) – 3x ² (x + 3) + 7x(x + 3) – 21x + 4x
= 2x ³ (x + 3) – 3x ² (x + 3) + 7x(x + 3) – 17x

To get the term -17x, multiply (x + 3) by -17 and add 51,
= 2x ³ (x + 3) – 3x ² (x + 3) + 7x(x+3) – 17(x + 3) + 51
= (x + 3) (2x ³ – 3x ² + 7x- 17) + 51
∴ Quotient = 2x ³ – 3x ² + 7x – 17,
Remainder = 51

v. Synthetic division:
(x ⁴ – 3x ² – 8) + (x + 4)
Dividend = x ⁴ – 3x ² – 8
∴ Index form = x ⁴ + 0x ³ – 3x ² + 0x – 8
∴ Coefficient form of the dividend = (1,0, -3,0, -8)
Divisor = x + 4
∴ Opposite of + 4 is -4

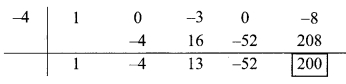
∴ Coefficient form of quotient = (1, -4, 13, -52)
∴ Quotient = x ³ – 4x ² + 13x – 52,
Remainder = 200

Linear division method:
x ⁴ – 3x ² – 8
To get the term x ⁴ , multiply (x + 4) by x ³ and subtract 4x ³ ,
= x ³ (x + 4) – 4x ³ – 3x ² – 8
= x ³ (x + 4) – 4x ³ – 3x ² – 8
To get the term – 4x ³ , multiply (x + 4) by -4x ² and add 16x ² ,
= x ³ (x + 4) – 4x ² (x + 4) + 16x ² – 3x ² – 8
= x ³ (x + 4) – 4x ² (x + 4) + 13x ² – 8
To get the term 13x ² , multiply (x + 4) by 13x and subtract 52x,
= x ³ (x + 4) – 4x ² (x + 4) + 13x(x + 4) – 52x – 8
= x ³ (x + 4) – 4x ² (x + 4) + 13x(x + 4) – 52x – 8
To get the term -52x, multiply (x + 4) by – 52 and add 208,
= x ³ (x + 4) – 4x ² (x + 4) + 13x(x + 4) – 52(x + 4) + 208 – 8
= (x + 4) (x ³ – 4x ² + 13x – 52) + 200
∴ Quotient = x ³ – 4x ² + 13x – 52,
Remainder 200

vi. Synthetic division:
(y ³ – 3y ² + 5y – 1) ÷ (y – 1)
Dividend = y ³ – 3y ² + 5y – 1
Coefficient form of the dividend = (1, -3, 5, -1)
Divisor = y – 1
∴Opposite of -1 is 1.

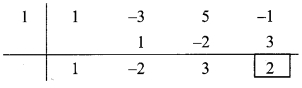
∴ Coefficient form of quotient = (1, -2, 3)
∴ Quotient = y ² – 2y + 3,
Remainder = 2

Linear division method:
y ³ -3y ² + 5y – 1
To get the term y ³ , multiply (y – 1) by y ² and add y ²
= y ² (y – 1) + y ² – 3y ² + 5y – 1
= y ² (y – 1) – 2y ² + 5y – 1
To get the term -2y ² , multiply (y – 1) by -2y and subtract 2y,
= y ² (y – 1) – 2y(y – 1) – 2y + 5y – 1
= y ² (y – 1) – 2y(y – 1) + 3y – 1
To get the term 3y, multiply (y – 1) by 3 and add 3,
= y ² (y – 1) – 2y(y – 1) + 3(y- 1) + 3 – 1
= (y – 1)(y ² – 2y + 3) + 2
∴ Quotient = y ² – 2y + 3,
Remainder = 2.