Practice Set 4.5 Algebra 9th Standard Maths Part 1 Chapter 4 Ratio and Proportion Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 4.5 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 4 Ratio and Proportion.

9th Standard Maths 1 Practice Set 4.5 Chapter 4 Ratio and Proportion Textbook Answers Maharashtra Board

Class 9 Maths Part 1 Practice Set 4.5 Chapter 4 Ratio and Proportion Questions With Answers Maharashtra Board

Question 1.
Which number should be subtracted from 12, 16 and 21 so that resultant numbers are in continued proportion?
Solution:
Let the number to be subtracted be x.
∴ (12 – x), (16 – x) and (21 – x) are in continued proportion.

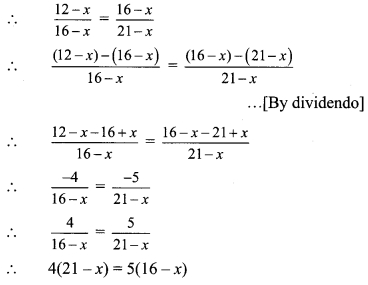
∴ 84 – 4x = 80 – 5x
∴ 5x – 4x = 80 – 84
∴ x = -4
∴ -4 should be subtracted from 12,16 and 21 so that the resultant numbers in continued proportion.

Question 2.
If (28 – x) is the mean proportional of (23 – x) and (19 – x), then find the value ofx.
Solution:
(28 – x) is the mean proportional of (23 – x) and (19-x). …[Given]

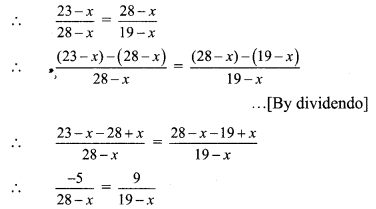
∴ -5(19 – x) = 9(28 – x)
∴ -95 + 5x = 252 – 9x
∴ 5x + 9x = 252 + 95
∴ 14x = 347
∴ x = \(\frac { 347 }{ 14 }\)

Question 3.
Three numbers are in continued proportion, whose mean proportional is 12 and the sum of the remaining two numbers is 26, then find these numbers.
Solution:
Let the first number be x.
∴ Third number = 26 – x
12 is the mean proportional of x and (26 – x).
∴ \(\frac { x }{ 12 }\) = \(\frac { 12 }{ 26 – x }\)
∴ x(26 – x) = 12 x 12
∴ 26x – x ² = 144
∴ x ² – 26x + 144 = 0
∴ x ² – 18x – 8x + 144 = 0
∴ x(x – 18) – 8(x – 18) = 0
∴ (x – 18) (x – 8) = 0
∴ x = 18 or x = 8
∴ Third number = 26 – x = 26 – 18 = 8 or 26 – x = 26 – 8 = 18
∴ The numbers are 18, 12, 8 or 8, 12, 18.

Question 4.
If (a + b + c)(a – b + c) = a ² + b ² + c ² , show that a, b, c are in continued proportion.
Solution:
(a + b + c)(a – b + c) = a ² + b ² + c ² …[Given]
∴ a(a – b + c) + b(a – b + c) + c(a – b + c) = a2 + b2 + c2
∴ a ² – ab + ac + ab – b ² + be + ac – be + c ² = a ² + b ² + c ²
∴ a ² + 2ac – b ² + c ² = a ² + b ² + c ²
∴ 2ac – b ² = b ²
∴ 2ac = 2b ²
∴ ac = b ²
∴ b ² = ac
∴ a, b, c are in continued proportion.

Question 5.
If \(\frac { a }{ b }\) = \(\frac { b }{ c }\) and a, b, c > 0, then show that,
i. (a + b + c)(b – c) = ab – c ²
ii. (a ² + b ² )(b ² + c ² ) = (ab + be) ²
iii. \(\frac{a^{2}+b^{2}}{a b}=\frac{a+c}{b}\)
Solution:
Let \(\frac { a }{ b }\) = \(\frac { b }{ c }\) = k
∴ b = ck
∴ a = bk =(ck)k
∴ a = ck ² …(ii)

i. (a + b + c)(b – c) = ab – c ²
L.H.S = (a + b + c) (b – c)
= [ck ² + ck + c] [ck – c] … [From (i) and (ii)]
= c(k ² + k + 1) c (k – 1)
= c ² (k ² + k + 1) (k – 1)
R.H.S = ab – c ²
= (ck ² ) (ck) – c ² … [From (i) and (ii)]
= c ² k ³ – c ²
= c ² (k ³ – 1)
= c ² (k – 1) (k ² + k + 1) … [a ³ – b ³ = (a – b) (a ² + ab + b ² ]
∴ L.H.S = R.H.S
∴ (a + b + c) (b – c) = ab – c ²

ii. (a ² + b ² )(b ² + c ² ) = (ab + bc) ²
b = ck; a = ck ²
L.H.S = (a ² + b ² ) (b ² + c ² )
= [(ck ² ) + (ck) ² ] [(ck) ² + c ² ] … [From (i) and (ii)]
= [c ² k ⁴ + c ² k ² ] [c ² k ² + c ² ]
= c ² k ² (k ² + 1) c ² (k ² + 1)
= c4k ² (k ² + 1) ²
R.H.S = (ab + bc) ²
= [(ck ² ) (ck) + (ck)c] ² …[From (i) and (ii)]
= [c ² k ³ + c ² k] ²
= [c ² k (k ² + 1)]2 = c ⁴ (k ² + 1) ²
∴ L.H.S = R.H.S
∴ (a ² + b ² ) (b ² + c ² ) = (ab + bc) ²

iii. \(\frac{a^{2}+b^{2}}{a b}=\frac{a+c}{b}\)

9th Standard Algebra Practice Set 4.5 Question 6. Find mean proportional of \(\frac{x+y}{x-y}, \frac{x^{2}-y^{2}}{x^{2} y^{2}}\).
Solution:
Let a be the mean proportional of \(\frac{x+y}{x-y}\) and \(\frac{x^{2}-y^{2}}{x^{2} y^{2}}\)