Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 5 Linear Equations in Two Variables.
9th Standard Maths 1 Practice Set 5.1 Chapter 5 Linear Equations in Two Variables Textbook Answers Maharashtra Board
Class 9 Maths Part 1 Practice Set 5.1 Chapter 5 Linear Equations in Two Variables Questions With Answers Maharashtra Board
Question 1.
By using variables x and y form any five linear equations in two variables.
Answer:
The general form of a linear equation in two variables x and y is ax + by + c = 0,
where a, b, c are real numbers and a ≠ 0, b ≠ 0.
Five linear equations in two variables are as follows:
i. 3x + 4y – 12 = 0
ii. 3x – 4y + 12 = 0
iii. 5x + 5y – 6 = 0
iv. 7x + 12y – 11 = 0
v. x – y + 5 = 0
Question 2.
Write five solutions of the equation x + y = 1.
Answer:
i. x = 1, y = 6
ii. x = -1, y = 8
iii. x = 5, y = 2
iv. x = 0, y = 7
v. x = 10, y = -3
Question 3.
Solve the following sets of simultaneous equations.
i. x + y = 4 ; 2x – 5y = 1
ii. 2x + y = 5 ; 3x – y = 5
iii. 3x – 5y = 16; x – 3y= 8
iv. 2y – x = 0; 10x + 15y = 105
v. 2x + 3y + 4 = 0; x – 5y = 11
vi. 2x – 7y = 7; 3x + y = 22
Solution:
i. Substitution Method:
x + y = 4
∴ x = 4 – y …(i)
2x – 5y = 1 ……(ii)
Substituting x = 4 – y in equation (ii),
2(4 – y) – 5y = 1
∴ 8 – 2y – 5y = 1
∴ 8 – 7y = 1
∴ 8 – 1 = 7y
∴ 7 = 7y
∴ y = \(\frac { 7 }{ 7 }\)
∴ y = 1
Substituting y = 1 in equation (i),
x = 4 – 1 = 3
∴ (3,1) is the solution of the given equations.
Alternate method:
Elimination Method:
x + y = 4 …(i)
2x – 5y = 1 ……(ii)
Multiplying equation (i) by 5,
5x + 5y = 20 … (iii)
Adding equations (ii) and (iii),
2x – 5y = 1
+ 5x + 5y = 20
7 = 21
∴ x = \(\frac { 21 }{ 7 }\)
∴ x = 3
Substituting x = 3 in equation (i),
3 + y = 4
∴ y = 4 – 3 = 1
(3,1) is the solution of the given equations.
ii. 2x + y = 5 …(i)
3x – y = 5 …(ii)
Adding equations (i) and (ii),
2x + y = 5
+ 3x – y = 5
5x = 10
∴ x = \(\frac { 10 }{ 5 }\)
∴ x = 2
Substituting x = 2 in equation (i),
2(2) + y = 5
4 + y = 5
∴ y = 5 – 4 = 1
∴ (2, 1) is the solution of the given equations.
iii. 3x – 5y = 16 …(i)
x – 3y = 8
∴x = 8 + 3y …..(ii)
Substituting x = 8 + 3y in equation (i),
3(8 + 3y) – 5y = 16
24 + 9y- 5y = 16
∴4y= 16 – 24
∴ 4y = -8
∴ y = \(\frac { -8 }{ 4 }\)
y = -2
Substituting y = -2 in equation (ii),
x = 8 + 3 (-2)
∴ x = 8 – 6 = 2
∴ (2, -2) is the solution of the given equations.
iv. 2y – x = 0
∴ x = 2y …(i)
10x + 15y = 105 …(ii)
Substituting x = 2y in equation (ii),
10(2y) + 15y = 105
∴ 20y + 15y = 105
∴ 35y = 105
∴ y = \(\frac { 105 }{ 35 }\)
∴ y = 3
Substituting y = 3 in equation (i),
x = 2y
∴ x = 2(3) = 6
∴ (6, 3) is the solution of the given equations.
v. 2x + 3y + 4 = 0 …(i)
x – 5y = 11
∴x = 11 + 5y …(ii)
Substituting x = 11 + 5y in equation (i),
2(11 +5y) + 3y + 4 = 0
∴ 22 + 10y + 3y + 4 = 0
∴ 13y + 26 = 0
∴ 13y = -26
∴y = \(\frac { -26 }{ 13 }\)
∴ y = -2
Substituting y = -2 in equation (ii),
x = 11 + 5y
∴ x = 11 + 5(-2)
∴ x = 11 – 10 = 1
∴ (1, -2) is the solution of the given equations.
vi. 2x – 7y = 7 …(i)
3x + y = 22
∴ y = 22 – 3x ……(ii)
Substituting y = 22 – 3x in equation (i),
2x – 7(22 – 3x) = 7
∴ 2x – 154 + 21x = 7
∴ 23x = 7 + 154
∴ 23x = 161
∴ x = \(\frac { 161 }{ 23 }\)
∴ x = 7
Substituting x = 7 in equation (ii),
y = 22 – 3x
∴ y = 22 – 3(7)
∴ 7 = 22 -21= 1
∴ (7, 1) is the solution of the given equations.
Question 1.
Solve the following equations. (Textbook pg. no. 80)
i. m + 3 = 5
ii. 3y + 8 = 22
iii. \(\frac { x }{ 3 }\) = 2
iv. 2p = p + \(\frac { 4 }{ 9 }\)
Solution:
i. m + 3 = 5
m = 5 – 3
∴m = 2
ii. 3y + 8 = 22
∴ 3y = 22 – 8
∴ 3y = 14
∴ y = \(\frac { 14 }{ 9 }\)
iii. \(\frac { x }{ 3 }\) = 2
∴ x = 2 × 3
∴ x = 6
iv. 2p = p + \(\frac { 4 }{ 9 }\)
∴ 2p – p = \(\frac { 4 }{ 9 }\)
∴ p = \(\frac { 4 }{ 9 }\)
Question 2.
Which number should be added to 5 to obtain 14? (Textbook pg. no. 80)
Solution:
x + 5 = 14
∴ x = 14 – 5
x = 9
∴ 9 + 5 = 14
Question 3.
Which number should be subtracted from 8 to obtain 2? (Textbook pg. no. 80)
Solution:
8 – y = 2
∴ y = 8 – 2
∴ y = 6
∴ 8 – 6 = 2
Question 4.
x + y = 5 and 2x + 2y= 10 are two equations in two variables. Find live different solutions of x + y = 5, verify whether same solutions satisfy the equation 2x + 2y = 10 also. Observe both equations. Find the condition where two equations in two variables have all solutions in common. (Textbook pg. no. 82)
Solution:
Five solutions of x + y = 5 are given below:
(1,4), (2, 3), (3, 2), (4,1), (0, 5)
The above solutions also satisfy the equation 2x + 2y = 10.
∴ x + y = 5 …[Dividing both sides by 2]
∴ If the two equations are the same, then the two equations in two variables have all solutions common.
Question 5.
3x – 4y – 15 = 0 and y + x + 2 = 0. Can these equations be solved by eliminating x ? Is the solution same? (Textbook pg. no. 84)
Solution:
3x – 4y – 15 = 0
∴ 3x – 4y = 15 …(i)
y + x + 2 = 0
∴ x + y = -2 ……(ii)
Multiplying equation (ii) by 3,
3x + 3y = -6 …(iii)
Subtracting equation (iii) from (i),
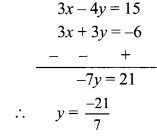
∴ y = -3
Substituting y = -3 in equation (ii),
∴ x – 3 = -2
∴ x = – 2 + 3
∴ x = 1
∴ (x, y) = ( 1, -3)
Yes, the given equations can be solved by eliminating x. Also, the solution will remain the same.