Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.5 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.
9th Standard Maths 2 Practice Set 5.5 Chapter 5 Quadrilaterals Textbook Answers Maharashtra Board
Class 9 Maths Part 2 Practice Set 5.5 Chapter 5 Quadrilaterals Questions With Answers Maharashtra Board
Question 1.
In the adjoining figure, points X, Y, Z are the midpoints of of ∆ABC respectively, cm. Find the lengths of side AB, side BC and side AC AB = 5 cm, AC = 9 cm and BC = 11c.m. Find the lengths of XY, YZ, XZ.
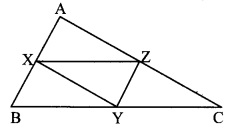
Solution:
i. AC = 9 cm [Given]
Points X and Y are the midpoints of sides AB and BC respectively. [Given]
∴ XY = \(\frac { 1 }{ 2 }\) AC [Midpoint tfyeprem]
= \(\frac { 1 }{ 2 }\) x 9 = 4.5 cm
ii. AB = 5 cm [Given]
Points Y and Z are the midpoints of sides BC and AC respectively. [Given]
∴ YZ = \(\frac { 1 }{ 2 }\) AB [Midpoint theorem]
= \(\frac { 1 }{ 2 }\) x 5 = 2.5 cm
iii. BC = 11 cm [Given]
Points X and Z are the midpoints of sides AB and AC respectively. [Given]
∴ XZ = \(\frac { 1 }{ 2 }\) BC [Midpoint theorem]
= \(\frac { 1 }{ 2 }\) x 11 = 5.5 cm
l(XY) = 4.5 cm, l(YZ) = 2.5 cm, l(XZ) = 5.5 cm
Question 2.
In the adjoining figure, □PQRS and □MNRL are rectangles. If point M is the midpoint of side PR, then prove that,
i. SL = LR
ii. LN = \(\frac { 1 }{ 2 }\) SQ.
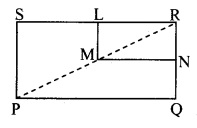
Given: □PQRS and □MNRL are rectangles. M is the midpoint of side PR.
Solution:
Toprove:
i. SL = LR
ii. LN = \(\frac { 1 }{ 2 }\) (SQ)
Proof:
i. □PQRS and □MNRL are rectangles. [Given]
∴ ∠S = ∠L = 90° [Angles of rectangles]
∠S and ∠L form a pair of corresponding angles on sides SP and LM when SR is their transversal.
∴eg ML || seg PS …(i) [Corresponding angles test]
In ∆PRS,
Point M is the midpoint of PR and seg ML || seg PS. [Given] [From (i)]
∴ Point L is the midpoint of seg SR. ……(ii) [Converse of midpoint theorem]
∴ SL = LR
ii. Similarly for ∆PRQ, we can prove that,
Point N is the midpoint of seg QR. ….(iii)
In ∆RSQ,
Points L and N are the midpoints of seg SR and seg QR respectively. [From (ii) and (iii)]
∴ LN = \(\frac { 1 }{ 2 }\)SQ [Midpoint theorem]
Question 3.
In the adjoining figure, ∆ABC is an equilateral triangle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ∆FED is an equilateral triangle.
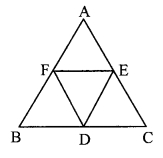
Given: ∆ABC is an equilateral triangle.
Points F, D and E are midpoints of side AB, side BC, side AC respectively.
To prove: ∆FED is an equilateral triangle.
Solution:
Proof:
∆ABC is an equilateral triangle. [Given]
∴ AB = BC = AC ….(i) [Sides of an equilateral triangle]
Points F, D and E are midpoints of side AB and BC respectively.
∴ FD = \(\frac { 1 }{ 2 }\)AC …..(ii) [Midpoint theorem]
Points D and E are the midpoints of sides BC and AC respectively.
∴ DE = \(\frac { 1 }{ 2 }\)AB …..(iii) [Midpoint theorem]
Points F and E are the midpoints of sides AB and AC respectively.
∴ FE = \(\frac { 1 }{ 2 }\)BC
∴ FD = DE = FE [From (i), (ii), (iii) and (iv) ]
∴ ∆FED is an equilateral triangle.
Question 4.
In the adjoining figure, seg PD is a median of ∆PQR. Point T is the midpoint of seg PD. Produced QT intersects PR at M. Show that \(\frac { PM }{ PR }\) = \(\frac { 1 }{ 3 }\). [Hint: Draw DN || QM]
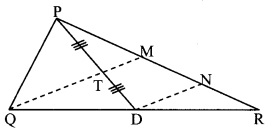
Solution:
Given: seg PD is a median of ∆PQR. Point T is the midpoint of seg PD.
To Prove: \(\frac { PM }{ PR }\) = \(\frac { 1 }{ 3 }\)
Construction: Draw seg DN ||seg QM such that P-M-N and M-N-R.
Proof:
In ∆PDN,
Point T is the midpoint of seg PD and seg TM || seg DN [Given]
∴ Point M is the midpoint of seg PN. [Construction and Q-T-M]
∴ PM = MN [Converse of midpoint theorem]
In ∆QMR,
Point D is the midpoint of seg QR and seg DN || seg QM [Construction]
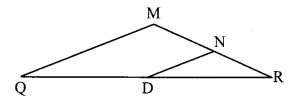
∴ Point N is the midpoint of seg MR. [Converse of midpoint theorem]
∴ RN = MN …..(ii)
∴ PM = MN = RN …..(iii) [From (i) and (ii)]
Now, PR = PM + MN + RN [ P-M-R-Q-T-M]
∴ PR = PM + PM + PM [From (iii) ]
∴ PR = 3PM
\(\frac { PM }{ PR }\) = \(\frac { 1 }{ 3 }\)