Practice Set 8.2 Geometry 9th Standard Maths Part 2 Chapter 8 Trigonometry Solutions Maharashtra Board

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 8.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 8 Trigonometry.

9th Standard Maths 2 Practice Set 8.2 Chapter 8 Trigonometry Textbook Answers Maharashtra Board

Class 9 Maths Part 2 Practice Set 8.2 Chapter 8 Trigonometry Questions With Answers Maharashtra Board

Question 1.
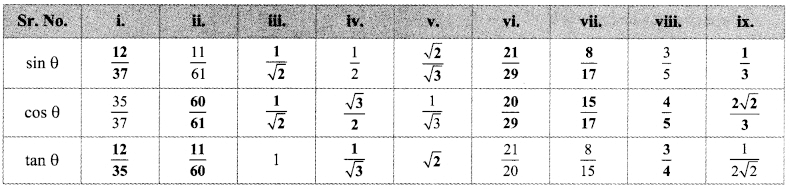
In the following table, a ratio is given in each column. Find the remaining two ratios in the column and complete the table.

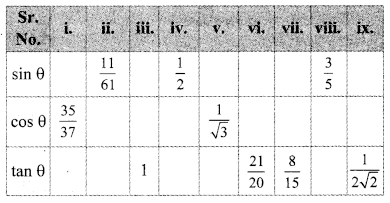
Solution:
i. cos θ = \(\frac { 35 }{ 37 }\) …(i) )[Given]
In right angled ∆ABC,

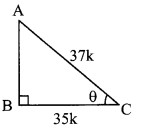
∠C = θ.

Let the common multiple be k.
∴ BC = 35k and AC = 37k
Now, AC ² = AB ² + BC ² …[Pythagoras theorem]
∴ (37k) ² = AB ² + (35k) ²
1369k ² = AB ² + 1225k ²
AB2 = 1369k ² – 1225k ²
= 144k ²
AB = 144k ²
AB = \(\sqrt { 2ghK }\) ² … [Taking square root of both sides]
= 12k

ii. sin θ = \(\frac { 11 }{ 61 }\) …..(i) [Given]
In right angled ∆ABC, ∠C = θ.


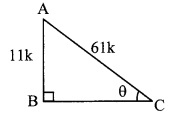
Let the common multiple be k.
AB = 11k and AC = 61k
Now, AC ² = AB ² + BC ² …[Pythagoras theorem]
∴ (61k) ² = (11k) ² + BC ²
∴ 3721k ² = 121k ² + BC ²
∴ BC ² = 3721k ² – 121k ² = 3600k ²
BC = \(\sqrt { 3600{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= 60k

iii. tan θ = 1 = \(\frac { 1 }{ 1 }\) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.


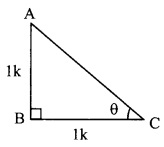
Let the common multiple be k.
∴ AB = 1k and BC = 1k
Now, AC ² = AB ² + BC ² …[Pythagoras theorem]
= K ² + K ²
= 2K ²
∴ AC = \(\sqrt { 2{ k }\)

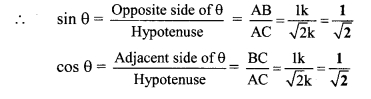
iv. sin θ = \(\frac { 1 }{ 2 }\) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.


Let the common multiple be k.
∴ AB = 1k and BC = 2k
Now, AC ² = AB ² + BC ² …[Pythagoras theorem]
∴ 2K ² = K ² + BC ²
∴ 4K ² = K ² + BC ²
∴ BC ² = 4K ² – K ² = 3K ²
∴ BC = \(\sqrt { 3{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= \(\sqrt { 3{ k }\)

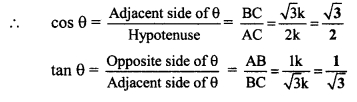
v. cos θ = \(\frac { 1 }{ \sqrt { 3 } } \) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.


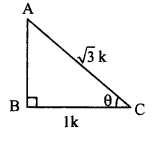
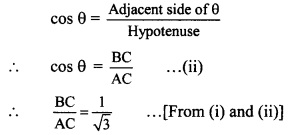
Let the common multiple be k.
∴ AB = 1k and BC = √3k
Now, AC ² = AB ² + BC ² …[Pythagoras theorem]
∴ (√3K) ² = AB ² + K ²
∴ 3K ² = 3K ² – K ² = 2K ²
∴ AB = \(\sqrt { 2{ k }^{ 2 } }\) .. .[Taking square root of both sides]
AB = √2K

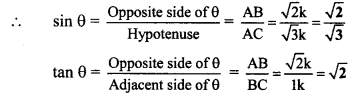
vi. cos θ = \(\frac { 21 }{ \sqrt { 20 } } \) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.


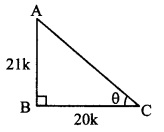
Let the common multiple be k.
∴ AB = 21k and BC = 20k
Now, AC ² = AB ² + BC ² …[Pythagoras theorem]
= (21)K ² + (20K) ²
= 441K ² – 400 ²
= 841K ²
∴ AB = \(\sqrt { 841{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= 29K

vii. tan θ = \(\frac { 8 }{ 15 } \) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.


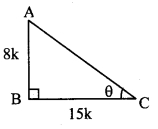
Let the common multiple be k.
∴ AB = 8k and BC = 15k
Now, AC ² = AB ² + BC ² …[Pythagoras theorem]
= (8)K ² + (15K) ²
= 64K ² – 225 ²
= 289K ²
∴ AC = \(\sqrt { 289{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= 17K

viii. sin θ = \(\frac { 3 }{ 5 } \) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.



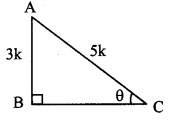
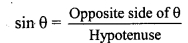
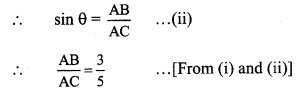
Let the common multiple be k.
∴ AB = 3k and AC = 5k
Now, AC ² = AB ² + BC ² …[Pythagoras theorem]
∴ (5)K ² = (3)K ² + BC ²
∴ 25K ² = 9K ² – 225 ²
∴ BC ² = 25K ² – 9K ²
∴ BC = \(\sqrt { 16{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= 4K

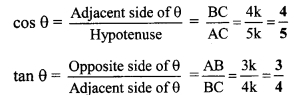
ix. tan θ = \(\frac { 1 }{ 2\sqrt { 2 } }\) ..(i) [Given]
In right angled ∆ABC,
∠C = θ.


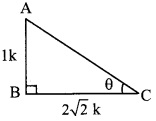
Let the common multiple be k.
∴ AB = 1k and AC = 2√2 k
Now, AC ² = AB ² + BC ² …[Pythagoras theorem]
= K ² + (2√2 k ) ²
= K ² – 225 ²
= 25K ² + 8K ²
= 9K ²
∴ AC = \(\sqrt { 9{ k }^{ 2 } }\) .. .[Taking square root of both sides]
= 3K

Question 2.
Find the values of:
i. 5 sin 30° + 3 tan 45°
ii. \(\frac { 4 }{ 5 }\)tan ² 60° + 3 sin ² 60°
iii. 2 sin 30° + cos 0° + 3 sin 90°
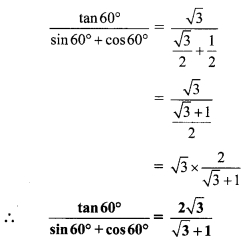
iv. \(\frac{\tan 60^{\circ}}{\sin 60^{\circ}+\cos 60^{\circ}}\)
v. cos ² 45° + sin ² 30°
vi. cos 60° x cos 30° + sin 60° x sin 30°
Solution:
i. sin 30° = \(\frac { 1 }{ 2 }\) and tan 45° = 1

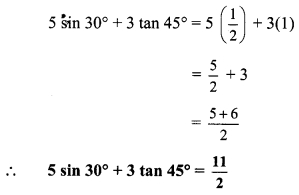
ii. \(\frac { 4 }{ 5 }\)tan ² 60° + 3 sin ² 60°

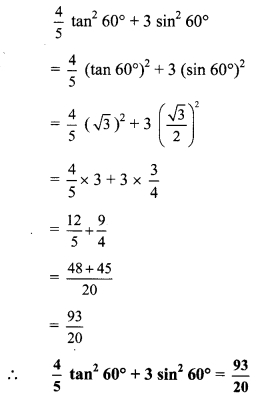
iii. 2 sin 30° + cos 0° + 3 sin 90°
2 sin 30° + cos0° + 3 sin 90° = 2 (\(\frac { 1 }{ 2 }\)) + 1 + 3(1)
= 1 + 1 + 3
∴ 2 sin 30° + cos 0° + 3 sin 90° = 5

iv. \(\frac{\tan 60^{\circ}}{\sin 60^{\circ}+\cos 60^{\circ}}\)

v. cos ² 45° + sin ² 30°

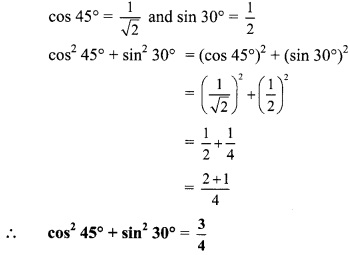
vi. cos 60° x cos 30° + sin 60° x sin 30°

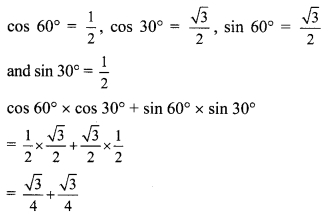
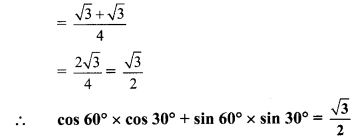
Question 3.
If sin θ = \(\frac { 4 }{ 5 }\) , then find cos θ.
Solution:
sin θ = \(\frac { 4 }{ 5 }\) .. .(i)[Given]
In right angled ∆ABC,
∠C = θ.


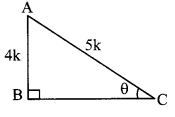
Let the common multiple be k.
∴ AB = 4k and AC = 5k
Now, AC ² = AB ² + BC ² … [Pythagoras theorem]
∴ (5 k) ² = (4k) ² + BC ²
∴ 25k ² = 16k ² + BC ²
∴ BC ² = 25k ² – 16k ² = 9k ²
∴ BC = \(\sqrt { 9{ k }^{ 2 } }\) . .[Taking square root of both sides]
= 3k

Question 4.
If cos θ = \(\frac { 15 }{ 17 }\) , then find sin θ.
Solution:
cos θ = \(\frac { 15 }{ 17 }\) .. .(i)[Given]
In right angled ∆ABC,
∠C = θ.


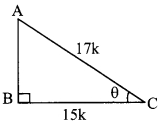
Let the common multiple be k.
∴ BC = 15k and AC = 17k
Now, AC ² = AB ² + BC ² … [Pythagoras theorem]
∴ (17 k) ² = AB ² + (15K) ²
∴ 289k ² = AB ² + 225 ²
∴ AB ² = 289k ² – 225k ²
= 64k ²
∴ AB = \(\sqrt { 64{ k }^{ 2 } }\) . .[Taking square root of both sides]
= 8k

Maharashtra Board Class 9 Maths Chapter 8 Trigonometry Practice Set 8.2 Intext Questions and Activities

Question 1.
In right angled ∆PQR, ∠Q = 900. Therefore ∠P and ∠R are complementary angles of each other. Verify the following ratios.
i. sin θ = cos (90 – θ)
ii. cos θ = sin (90 – θ)
iii. sin 30° = cos (90° – 30°) = cos 60°
iv. cos 30° = sin (90° – 30°) = sin 60° (Textbook pg. no. 107)
Solution:
In ∆PQR, ∠Q = 90°, ∠P = θ
∴ ∠R = 90 – θ

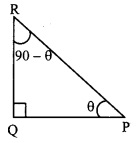
i. sin θ = cos (90 – θ)

ii. cos θ = sin (90 – θ)

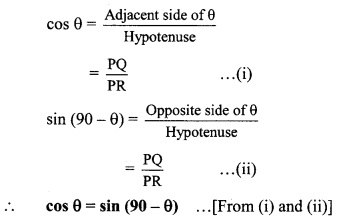
iii. Let ∠P = θ = 30°
∴ ∠R = 90° – 30°

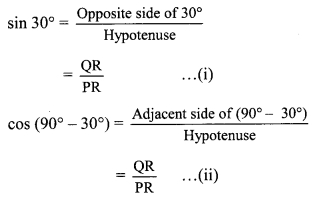
sin 30° = cos (90° – 30°) … [From (i) and (ii)]
sin 30° = cos 60°

iv. cos 30° = sin (90° – 30°) = sin 60°

∴ cos 30° = sin (90° – 30°) .,.[From (i) and (ii)]
∴ cos 30° = sin 60°

Question 2.
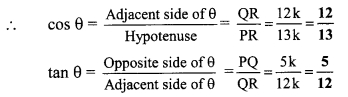
In right angled ∆PQR, ∠Q = 90°, ∠R = θ and if sin θ = \(\frac { 5 }{ 13 }\), then find cos θ and tan θ. (Textbook pg. no. 110)
Solution:
i. Take the given trigonometric ratio as 13k equation (i).
sin θ = \(\frac { 5 }{ 13 }\) .. .(i)[Given]
By using the definition write the trigonometric ratio of sin O and take it as equation (ii).
In right angled ∆PQR, ∠R = θ


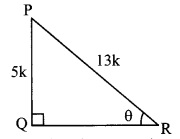
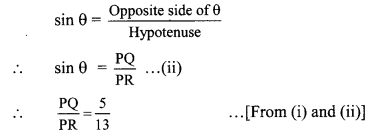
Let the common multiple be k.
∴ PQ = 5k and PR = 13k
Find QR by using Pythagoras theorem.
PR ² = PQ ² + QR ² … [Pythagoras theorem]
∴ (13k) ² = (5k) ² + QR ²
∴ 169k ² = 25k ² + QR ²
∴ QR ² = 169k ² – 25k ²
= 144k ²
∴ QR = \(\sqrt { 144{ k }^{ 2 } }\) . . . [Taking square root of both sides]
= 12k

Question 3.
While solving the above Illustrative example, why the lengths of PQ and PR are taken 5k and 13k? (Textbook pg. no. 111)
Solution:
\(\frac { PQ }{ PR }\) = \(\frac { 5 }{ 13 }\) … [Given]
Here, the ratio of the lengths of sides PQ and PR is 5 : 13.
The actual lengths of the sides can be any multiple of the ratio. Hence, we consider the multiple k while solving.

Question 4.
While solving the above illustrative example, can we take the lengths of PQ and PR as 5 and 13? If so, then what changes are needed In the writing of the solution. (Tcxtbook pg. no. 111)
Solution:
Yes, we can take lengths of PQ and PR as 5 and 13.
In that case, we will have to take k = 1 and solve the problem accordingly.

Question 5.
Verify that the equation ‘sin ² θ + cos ² θ = 1’ is true when θ = 0° or θ = 90°.
(Textbook pg. no. 112)
Solution:
sin ² θ + cos ² θ = 1
i. lf θ = 0°,
LH.S. = sin ² θ + cos ² θ
= sin ² 0° + cos ² 0°
= 0 + 1 …[∵ sin 0° = 0, cos 0° = 1]
= R.H.S.
∴ sin ² θ + cos ² θ = 1

ii. If θ = 90°,
L.H.S.= sin ² θ +cos ² θ
= sin ² 90° + cos ² 90°
= 1 + 0 … [ ∵ sin 90° = 1, cos 90° = 0]
= 1
= R.H.S.
∴ sin ² θ + cos ² θ = 1