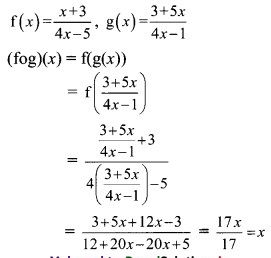11th Commerce Maths 1 Chapter 2 Miscellaneous Exercise 2 Answers Maharashtra Board

Functions Class 11 Commerce Maths 1 Chapter 2 Miscellaneous Exercise 2 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 2 Functions Miscellaneous Exercise 2 Questions and Answers.

Std 11 Maths 1 Miscellaneous Exercise 2 Solutions Commerce Maths

Question 1.
Which of the following relations are functions? If it is a function determine its domain and range.
(i) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5) (12, 6), (14, 7)}
(ii) {(0, 0), (1, 1), (1, -1), (4, 2), (4, -2), (9, 3), (9, -3), (16, 4), (16, -4)}
(iii) {(1, 1), (3, 1), (5, 2)}
Solution:
(i) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5) (12, 6), (14, 7)}

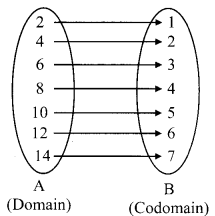
Every element of set A has been assigned a unique element in set B.
∴ Given relation is a function.
Domain = {2, 4, 6, 8, 10, 12, 14},
Range = {1, 2, 3, 4, 5, 6, 7}

(ii) {(0, 0), (1, 1), (1, -1), (4, 2), (4, -2), (9, 3), (9, -3), (16, 4), (16, -4)}
∴ (1, 1), (1, -1) ∈ the relation
∴ Given relation is not a function.
As element 1 of the domain has not been assigned a unique element of co-domain.

(iii) {(1, 1), (3, 1), (5, 2)}

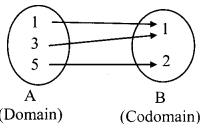
Every element of set A has been assigned a unique element in set B.
∴ Given relation is a function.
Domain = {1, 3, 5}, Range = {1, 2}

Question 2.
A function f: R → R defined by f(x) = \(\frac{3 x}{5}\) + 2, x ∈ R. Show that f is one-one and onto. Hence, find f ^-1 .
Solution:
f: R → R defined by f(x) = \(\frac{3 x}{5}\) + 2
First we have to prove that f is one-one function for that we have to prove if
f(x ₁ ) = f(x ₂ ) then x ₁ = x ₂
Here f(x) = \(\frac{3 x}{5}\) + 2
Let f(x ₁ ) = f(x ₂ )
∴ \(\frac{3 x_{1}}{5}+2=\frac{3 x_{2}}{5}+2\)
∴ \(\frac{3 x_{1}}{5}=\frac{3 x_{2}}{5}\)
∴ x ₁ = x ₂
∴ f is a one-one function.
Now, we have to prove that f is an onto function.
Let y ∈ R be such that
y = f(x)
∴ y = \(\frac{3 x}{5}\) + 2
∴ y – 2 = \(\frac{3 x}{5}\)
∴ x = \(\frac{5(y-2)}{3}\) ∈ R
∴ for any y ∈ co-domain R, there exist an element x = \(\frac{5(y-2)}{3}\) ∈ domain R such that f(x) = y
∴ f is an onto function.
∴ f is one-one onto function.
∴ f ^-1 exists.
∴ \(\mathrm{f}^{-1}(y)=\frac{5(y-2)}{3}\)
∴ \(f^{-1}(x)=\frac{5(x-2)}{3}\)

Question 3.
A function f is defined as follows:
f(x) = 4x + 5, for -4 ≤ x < 0. Find the values of f(-1), f(-2), f(0), if they exist.
Solution:
f(x) = 4x + 5, -4 ≤ x < 0
f(-1) = 4(-1) + 5 = -4 + 5 = 1
f(-2) = 4(-2) + 5 = -8 + 5 = -3
x = 0 ∉ domain of f
∴ f(0) does not exist.

Question 4.
A function f is defined as follows:
f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3.
Solution:
f(x) = 5 – x
f(x) = 3
∴ 5 – x = 3
∴ x = 5 – 3 = 2

Question 5.
If f(x) = 3x ² – 5x + 7, find f(x – 1).
Solution:
f(x) = 3x ² – 5x + 7
∴ f(x – 1) = 3(x – 1) ² – 5(x – 1) + 7
= 3(x ² – 2x + 1) – 5(x – 1) + 7
= 3x ² – 6x + 3 – 5x + 5 + 7
= 3x ² – 11x + 15

Question 6.
If f(x) = 3x + a and f(1) = 7, find a and f(4).
Solution:
f(x) = 3x + a,
f(1) = 7
∴ 3(1) + a = 7
∴ a = 7 – 3 = 4
∴ f(x) = 3x + 4
∴ f(4) = 3(4) + 4
= 12 + 4
= 16

Question 7.
If f(x) = ax ² + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
Solution:
f(x) = ax ² + bx + 2
f(1) = 3
∴ a(1) ² + b(1) + 2 = 3
∴ a + b = 1 …….(i)
f(4) = 42
∴ a(4) ² + b(4) + 2 = 42
∴ 16a + 4b = 40
Dividing by 4, we get
4a + b = 10 ……….(ii)
Solving (i) and (ii), we get
a = 3, b = -2

Question 8.
If f(x) = \(\frac{2 x-1}{5 x-2}, x \neq \frac{2}{5}\), verify whether (fof)(x) = x
Solution:
(fof)(x) = f(f(x))

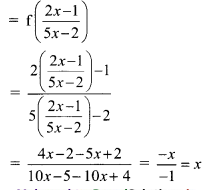
Question 9.
If f(x) = \(\frac{x+3}{4 x-5}\), g(x) = \(\frac{3+5 x}{4 x-1}\), then verify that (fog)(x) = x.
Solution: