Complex Numbers Class 11 Commerce Maths 1 Chapter 3 Exercise 3.1 Answers Maharashtra Board
Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 3 Complex Numbers Ex 3.1 Questions and Answers.
Std 11 Maths 1 Exercise 3.1 Solutions Commerce Maths
Question 1.
Write the conjugates of the following complex numbers:
(i) 3 + i
(ii) 3 – i
(iii) -√5 – √7i
(iv) -√-5
(v) 5i
(vi) √5 – i
(vii) √2 + √3i
Solution:
(i) Conjugate of (3 + i) is (3 – i)
(ii) Conjugate of (3 – i) is (3 + i)
(iii) Conjugate of (-√5 – √7i) is (-√5 + √7i)
(iv) -√-5 = -√5 × √-1 = -√5i
Conjugate of -√-5 is √5i
(v) Conjugate of 5i is -5i
(vi) Conjugate of √5 – i is √5 + i
(vii) Conjugate of √2 + √3i is √2 – √3i

Question 2.
Express the following in the form of a + ib, a, b ∈ R, i = √-1. State the values of a and b:
(i) (1 + 2i)(-2 + i)
(ii) \(\frac{\mathrm{i}(4+3 \mathrm{i})}{(1-\mathrm{i})}\)
(iii) \(\frac{(2+i)}{(3-i)(1+2 i)}\)
(iv) \(\frac{3+2 i}{2-5 i}+\frac{3-2 i}{2+5 i}\)
(v) \(\frac{2+\sqrt{-3}}{4+\sqrt{-3}}\)
(vi) (2 + 3i)(2 – 3i)
(vii) \(\frac{4 i^{8}-3 i^{9}+3}{3 i^{11}-4 i^{10}-2}\)
Solution:
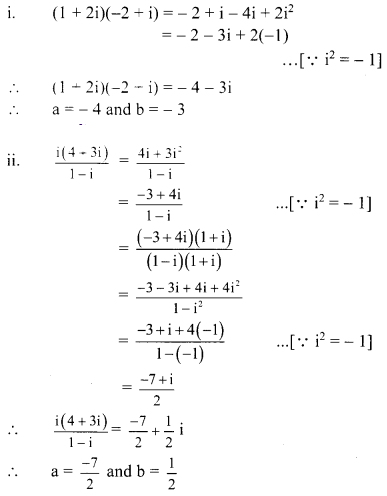
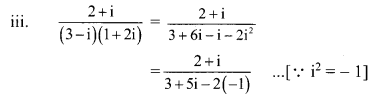
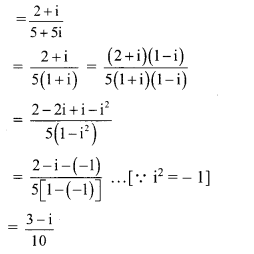
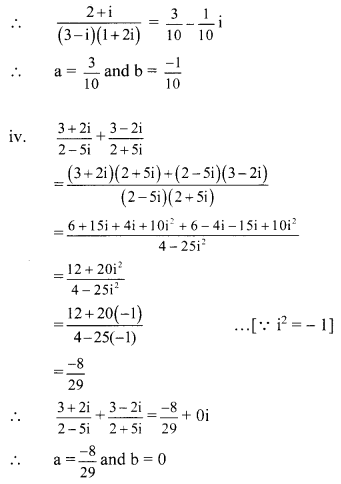
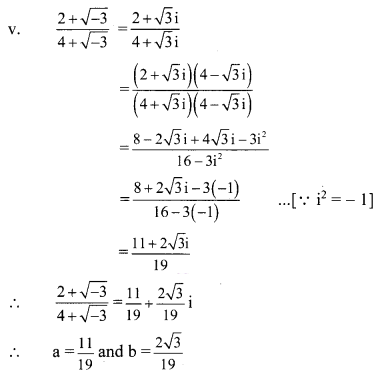
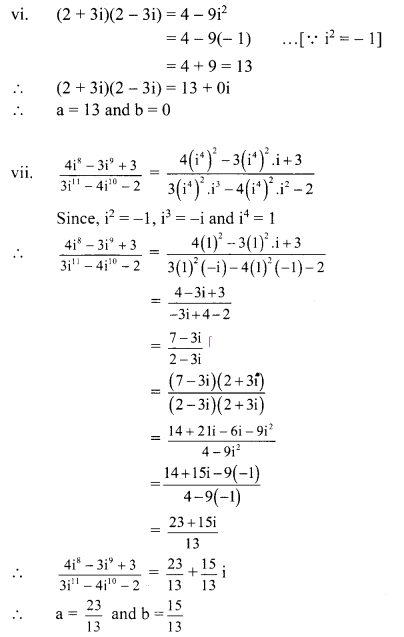
Question 3.
Show that (-1 + √3i)
3
is a real number.
Solution:
(-1 + √3i)
3
= (-1)
3
+ 3(-1)
2
(√3i) + 3(-1)(√3i)
2
+(√3i)
3
[∵ (a + b)
3
= a
3
+ 3a
2
b + 3ab
2
+ b
3
]
= -1 + 3√3i – 3(3i
2
) + 3√3 i
3
= -1 + 3√3i – 3(-3) – 3√3i [∵ i
2
= -1, i
3
= -1]
= -1 + 9
= 8, which is a real number.
Question 4.
Evaluate the following:
(i) i
35
(ii) i
888
(iii) i
93
(iv) i
116
(v) i
403
(vi) \(\frac{1}{i^{58}}\)
(vii) i
30
+ i
40
+ i
50
+ i
60
Solution:
We know that, i
2
= -1, i
3
= -i, i
4
= 1
(i) i
35
= (i
4
)
8
(i
2
) i = (1)
8
(-1) i = -i
(ii) i
888
= (i
4
)
222
= (1)
222
= 1
(iii) i
93
= (i
4
)
23
. i = (1)
23
. i = i
(iv) i
116
= (i
4
)
29
= (1)
29
= 1
(v) i
403
= (i
4
)
100
(i
2
) i = (1)
100
(-1) i = -i
(vi) \(\frac{1}{i^{88}}=\frac{1}{\left(i^{4}\right)^{14} \cdot i^{2}}=\frac{1}{(1)^{14}(-1)}=-1\)
(vii) i
30
+ i
40
+ i
50
+ i
60
= (i
4
)
7
i
2
+ (i
4
)
10
+ (i
4
)
12
i
2
+ (i
4
)
15
= (1)
7
(-1) + (1)
10
+ (1)
12
(-1) + (1)
15
= -1 + 1 – 1 + 1
= 0

Question 5.
Show that 1 + i
10
+ i
20
+ i
30
is a real number.
Solution:
1 + i
10
+ i
20
+ i
30
= 1 + (i
4
)
2
. i
2
+ (i
4
)
5
+ (i
4
)
7
. i
2
= 1 + (1)
2
(-1) + (1)
5
+ (1)
7
(-1) [∵ i
4
= 1, i
2
= -1]
= 1 – 1 + 1 – 1
= 0, which is a real number.
Question 6.
Find the value of
(i) i
49
+ i
68
+ i
89
+ i
110
(ii) i + i
2
+ i
3
+ i
4
Solution:
(i) i
49
+ i
68
+ i
89
+ i
110
= (i
4
)
12
. i + (i
4
)
17
+ (i
4
)
22
. i + (i
4
)
27
. i
2
= (1)
12
. i + (1)
17
+ (1)
22
. i + (1)
27
(-1) ……[∵ i
4
= 1, i
2
= -1]
= i + 1 + i – 1
= 2i
(ii) i + i
2
+ i
3
+ i
4
= i + i
2
+ i
2
. i + i
4
= i – 1 – i + 1 [∵ i
2
= -1, i
4
= 1]
= 0
Question 7.
Find the value of 1 + i
2
+ i
4
+ i
6
+ i
8
+ …… + i
20
.
Solution:
1 + i
2
+ i
4
+ i
6
+ i
8
+ ….. + i
20
= 1 + (i
2
+ i
4
) + (i
6
+ i
8
) + (i
10
+ i
12
) + (i
14
+ i
16
) + (i
18
+ i
20
)
= 1 + [i
2
+ (i
2
)
2
] + [(i
2
)
3
+ (i
2
)
4
] + [(i
2
)
5
+ (i
2
)
6
] + [(i
2
)
7
+ (i
2
)
8
] + [(i
2
)
9
+ (i
2
)
10
]
= 1 + [-1 + (- 1)
2
] + [(-1)
3
+ (-1)
4
] + [(-1)
5
+ (-1)
6
] + [(-1)
7
+ (-1)
8
] + [(-1)
9
+ (-1)
10
] [∵ i
2
= -1]
= 1 + (-1 + 1) + (-1 + 1) + (-1 + 1) + (-1 + 1) + (-1 + 1)
= 1 + 0 + 0 + 0 + 0 + 0
= 1
Question 8.
Find the values of x and y which satisfy the following equations (x, y ∈ R):
(i) (x + 2y) + (2x – 3y)i + 4i = 5
(ii) \(\frac{x+1}{1+\mathrm{i}}+\frac{y-1}{1-\mathrm{i}}=\mathrm{i}\)
Solution:
(i) (x + 2y) + (2x – 3y)i + 4i = 5
∴ (x + 2y) + (2x – 3y)i = 5 – 4i
Equating real and imaginary parts, we get
x + 2y = 5 ……..(i)
and 2x – 3y = -4 ………(ii)
Equation (i) × 2 – equation (ii) gives
7y = 14
∴ y = 2
Putting y- 2 in (i), we get
x + 2(2) = 5
∴ x + 4 = 5
∴ x = 1
∴ x = 1 and y = 2
Check:
If x = 1 and y = 2 satisfy the given condition, then our answer is correct.
L.H.S. = (x + 2y) + (2x – 3y)i + 4i
= (1 + 4) + (2 – 6)i + 4i
= 5 – 4i + 4i
= 5
= R.H.S.
Thus, our answer is correct.
(ii) \(\frac{x+1}{1+\mathrm{i}}+\frac{y-1}{1-\mathrm{i}}=\mathrm{i}\)
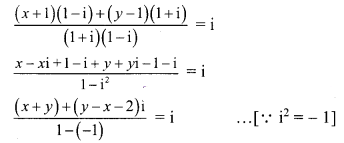
(x + y) + (y – x – 2)i = 2i
(x + y) + (y – x – 2)i = 0 + 2i
Equating real and imaginary parts, we get
x + y = 0 and y – x – 2 = 2
∴ x + y = 0 ……(i)
and -x + y = 4 ……..(ii)
Adding (i) and (ii), we get
2y = 4
∴ y = 2
Putting y = 2 in (i), we get
x + 2 = 0
∴ x = -2
∴ x = -2 and y = 2

Question 9.
Find the value of:
(i) x
3
– x
2
+ x + 46, if x = 2 + 3i
(ii) 2x
3
– 11x
2
+ 44x + 27, if x = \(\frac{25}{3-4 i}\)
Solution:
(i) x = 2 + 3i
∴ x – 2 = 3i
∴ (x – 2)
2
= 9i
2
∴ x
2
– 4x + 4 = 9(-1) …..[∵ i
2
= -1]
∴ x
2
– 4x + 13 = 0 ……(i)
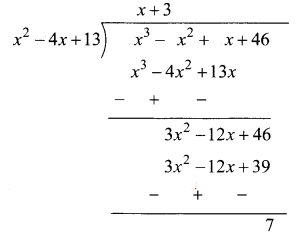
∴ x
3
– x
2
+ x + 46 = (x
2
– 4x + 13)(x + 3) + 7
= 0(x + 3) + 7 ……[From (i)]
= 7
(ii) x = \(\frac{25}{3-4 i}\)
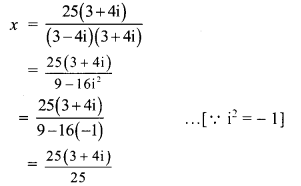
∴ x = 3 + 4i
∴ x – 3 = 4i
∴ (x – 3)
2
= 16i
2
∴ x
2
– 6x + 9 = 16(-1) …….[∵ i
2
= -1]
∴ x
2
– 6x + 25 = 0 …….(i)
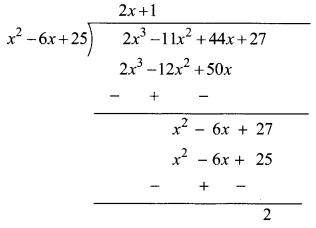
∴ 2x
3
– 11x
2
+ 44x + 27
= (x
2
– 6x + 25) (2x + 1) + 2
= 0 . (2x + 1) + 2 ……[From (i)]
= 0 + 2
= 2