11th Commerce Maths 1 Chapter 3 Exercise 3.3 Answers Maharashtra Board

Complex Numbers Class 11 Commerce Maths 1 Chapter 3 Exercise 3.3 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 3 Complex Numbers Ex 3.3 Questions and Answers.

Std 11 Maths 1 Exercise 3.3 Solutions Commerce Maths

Question 1.
If ω is a complex cube root of unity, show that
(i) (2 – ω)(2 – ω ² ) = 7
(ii) (2 + ω + ω ² ) ³ – (1 – 3ω + ω ² ) ³ = 65
(iii) \(\frac{\left(\mathbf{a}+\mathbf{b} \omega+\mathbf{c} \omega^{2}\right)}{\mathbf{c}+\mathbf{a} \omega+\mathbf{b} \omega^{2}}\) = ω ²
Solution:
ω is the complex cube root of unity.
∴ ω ³ = 1 and 1 + ω + ω ² = 0
Also, 1 + ω ² = -ω, 1 + ω = -ω ² and ω + ω ² = -1
(i) L.H.S. = (2 – ω)(2 – ω ² )
= 4 – 2ω ² – 2ω + ω ³
= 4 – 2(ω ² + ω) + 1
= 4 – 2(-1) + 1
= 4 + 2 + 1
= 7
= R.H.S.

(ii) L.H.S. = (2 + ω + ω ² ) ³ – (1 – 3ω + ω ² ) ³
= [2 + (ω + ω ² )] ³ – [-3ω + (1 + ω ² )] ³
= (2 – 1) ³ – (-3ω – ω) ³
= 13 – (-4ω) ³
= 1 + 64ω ³
= 1 + 64(1)
= 65
= R.H.S.

(iii) L.H.S. =\(\frac{\left(\mathbf{a}+\mathbf{b} \omega+\mathbf{c} \omega^{2}\right)}{\mathbf{c}+\mathbf{a} \omega+\mathbf{b} \omega^{2}}\)
= \(\frac{a \omega^{3}+b \omega^{4}+c \omega^{2}}{c+a \omega+b \omega^{2}}\) ……[∵ ω ³ = 1, ω ⁴ = ω]
= \(\frac{\omega^{2}\left(c+a \omega+b \omega^{2}\right)}{c+a \omega+b \omega^{2}}\)
= ω ²
= R.H.S.

Question 2.
If ω is a complex cube root of unity, find the value of
(i) ω + \(\frac{1}{\omega}\)
(ii) ω ² + ω ³ + ω ⁴
(iii) (1 + ω ² ) ³
(iv) (1 – ω – ω ² ) ³ + (1 – ω + ω ² ) ³
(v) (1 + ω)(1 + ω ² )(1 + ω ⁴ )(1 + ω ⁸ )
Solution:
ω is the complex cube root of unity.
∴ ω ³ = 1 and 1 + ω + ω ² = 0
Also, 1 + ω ² = -ω, 1 + ω = -ω ² and ω + ω ² = -1
(i) ω + \(\frac{1}{\omega}\)
= \(\frac{\omega^{2}+1}{\omega}\)
= \(\frac{-\omega}{\omega}\)
= -1

(ii) ω ² + ω ³ + ω ⁴
= ω ² (1 + ω + ω ² )
= ω ² (0)
= 0

(iii) (1 + ω ² ) ³
= (-ω) ³
= -ω ³
= -1

(iv) (1 – ω – ω ² ) ³ + (1 – ω + ω ² ) ³
= [1 – (ω + ω ² )] ³ + [(1 + ω ² ) – ω] ³
= [1 – (-1)] ³ + (-ω – ω) ³
= 2 ³ + (-2ω) ³
= 8 – 8ω ³
= 8 – 8(1)
= 0

(v) (1 + ω)(1 + ω ² )(1 + ω ⁴ )(1 + ω ⁸ )
= (1 + ω)(1 + ω ² )(1 + ω)(1 + ω ² ) …..[∵ ω ³ = 1, ω ⁴ = ω]
= (-ω ² )(-ω)(-ω ² )(-ω)
= ω ⁶
= (ω ³ ) ²
= (1) ²
= 1

Question 3.
If α and β are the complex cube roots of unity, show that α ² + β ² + αβ = 0.
Solution:
α and β are the complex cube roots of unity.

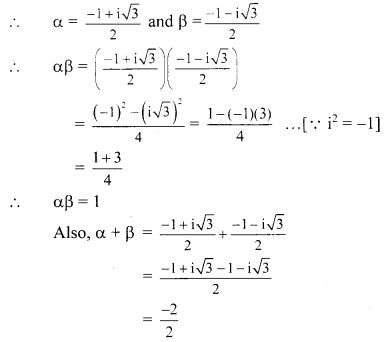
∴ α – β = -1
L.H.S. = α ² + β ² + αβ
= α ² + 2αβ + β ² + αβ – 2αβ ……[Adding and subtracting 2αβ]
= (α ² + 2αβ + β ² ) – αβ
= (α + β) ² – αβ
= (-1) ² – 1
= 1 – 1
= 0
= R.H.S.

Question 4.
If x = a + b, y = αa + βb and z = aβ + bα, where α and β are the complex cube roots of unity, show that xyz = a ³ + b ³ .
Solution:
x = a + b, y = αa + βb, z = aβ + bα
α and β are the complex cube roots of unity.

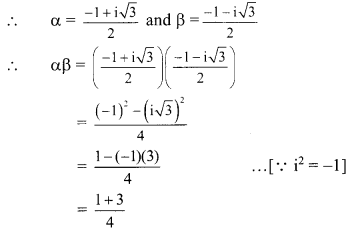
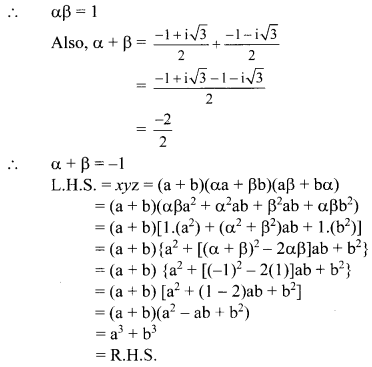
Question 5.
If ω is a complex cube root of unity, then prove the following:
(i) (ω ² + ω – 1) ³ = -8
(ii) (a + b) + (aω + bω ² ) + (aω ² + bω) = 0
Solution:
ω is the complex cube root of unity.
∴ ω ³ = 1 and 1 + ω + ω ² = 0
Also, 1 + ω ² = -ω, 1 + ω = -ω ² and ω + ω ² = -1
(i) L.H.S. = (ω ² + ω – 1) ³
= (-1 – 1) ³
= (-2) ³
= -8
= R.H.S.

(ii) L.H.S. = (a + b) + (aω + bω ² ) + (aω ² + bω)
= (a + aω + aω ² ) + (b + bω + bω ² )
= a(1 + ω + ω ² ) + b(1 + ω + ω ² )
= a(0) + b(0)
= 0
= R.H.S.