Complex Numbers Class 11 Commerce Maths 1 Chapter 3 Miscellaneous Exercise 3 Answers Maharashtra Board
Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 3 Complex Numbers Miscellaneous Exercise 3 Questions and Answers.
Std 11 Maths 1 Miscellaneous Exercise 3 Solutions Commerce Maths
Question 1.
Find the value of \(\frac{i^{592}+i^{590}+i^{588}+i^{586}+i^{584}}{i^{582}+i^{580}+i^{578}+i^{576}+i^{574}}\)
Solution:
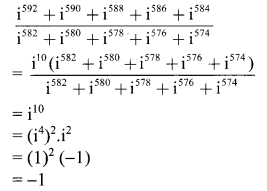
Question 2.
Find the value of √-3 × √-6.
Solution:
√-3 × √-6 = √3 × √-1 + √6 × √-1
= √3i × √6i
= √18i
2
= -3√2 ……[∵ i
2
= -1]

Question 3.
Simplify the following and express in the form a + ib.
(i) 3 + √-64
(ii) (2i
3
)
2
(iii) (2 + 3i) (1 – 4i)
(iv) \(\frac{5}{2}\) i(-4 – 3i)
(v) (1 + 3i)2 (3 + i)
(vi) \(\frac{4+3 i}{1-i}\)
(vii) \(\left(1+\frac{2}{i}\right)\left(3+\frac{4}{i}\right)(5+i)^{-1}\)
(viii) \(\frac{\sqrt{5}+\sqrt{3} i}{\sqrt{5}-\sqrt{3} i}\)
(ix) \(\frac{3 i^{5}+2 i^{7}+i^{9}}{i^{6}+2 i^{8}+3 i^{18}}\)
(x) \(\frac{5+7 i}{4+3 i}+\frac{5+7 i}{4-3 i}\)
Solution:
(i) 3 + √-64
= 3 + √64 . √-1
= 3 + 8i
(ii) (2i
3
)
2
= 4i
6
= 4(i
2
)
3
= 4(-1)
3
…..[∵ i
2
= -1]
= -4
= -4 + 0i
(iii) (2 + 3i)(1 – 4i) = 2 – 8i + 3i – 12i
2
= 2 – 5i – 12(-1) ……[∵ i
2
= -1]
= 14 – 5i
(iv) \(\frac{5}{2}\) i(-4 – 3i)
= \(\frac{5}{2}\) (-4i – 3i
2
)
= \(\frac{5}{2}\) [-4i – 3(-1)] ……[∵ i
2
= -1]
= \(\frac{5}{2}\) (3 – 4i)
= \(\frac{15}{2}\) – 10i

(v) (1 + 3i)
2
(3 + i)
= (1 + 6i + 9i
2
) (3 + i)
= (1 + 6i – 9)(3 + i) ……[∵ i
2
= -1]
= (-8 + 6i)(3 + i)
= -24 – 8i + 18i + 6i
2
= -24 + 10i + 6(-1)
= -24 + 10i – 6
= -30 + 10i
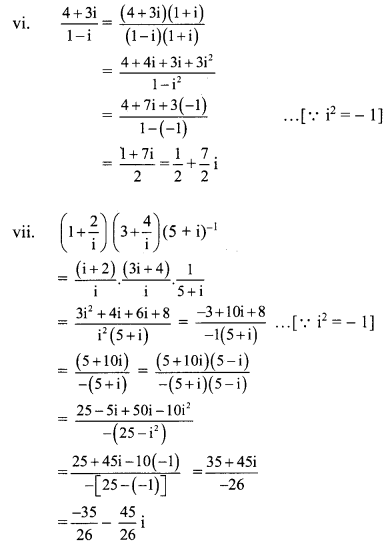
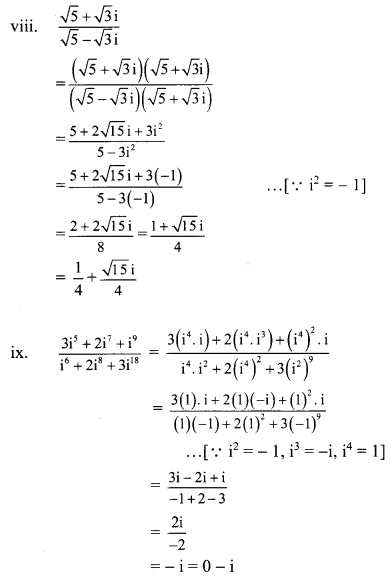
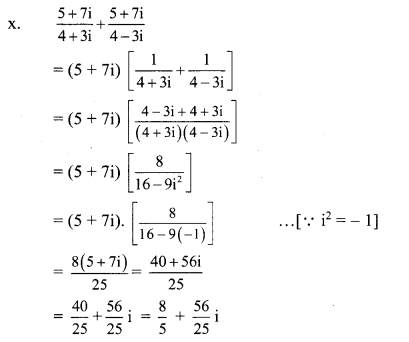
Question 4.
Solve the following equations for x, y ∈ R:
(i) (4 – 5i) x + (2 + 3i) y = 10 – 7i
(ii) (1 – 3i) x + (2 + 5i) y = 1 + i
(iii) \(\frac{x+i y}{2+3 i}\) = 7 – i
(iv) (x + iy) (5 + 6i) = 2 + 3i
(v) 2x + i
9
y (2 + i) = x i
7
+ 10 i
16
Solution:
(i) (4 – 5i) x + (2 + 3i)y = 10 – 7i
∴ (4x + 2y) + (3y – 5x) i = 10 – 7i
Equating real and imaginary parts, we get
4x + 2y = 10
i.e., 2x + y = 5 …….(i)
and 3y – 5x = -7 ……..(ii)
Equation (i) × 3 – equation (ii) gives
11x = 22
∴ x = 2
Putting x = 2 in (i), we get
2(2) + y = 5
∴ y = 1
∴ x = 2 and y = 1
(ii) (1 – 3i) x + (2 + 5i) y = 7 + i
∴ (x + 2y) + (-3x + 5y)i = 7 + i
Equating real and imaginary parts, we get
x + 2y = 7 ……..(i)
and -3x + 5y = 1 ……..(ii)
Equation (i) × 3 + equation (ii) gives
11y = 22
∴ y = 2
Putting y = 2 in (i), we get
x + 2(2) = 7
∴ x = 3
∴ x = 3 and y = 2

(iii) \(\frac{x+i y}{2+3 i}\) = 7 – i
∴ x + iy = (7 – i)(2 + 3i)
∴ x + iy = 14 + 21i – 2i – 3i
2
∴ x + iy = 14 + 19i – 3(-1) …..[∵ i
2
= -1]
∴ x + iy = 17 + 19i
Equating real and imaginary parts, we get
x = 17 and y = 19
(iv) (x + iy)(5 + 6i) = 2 + 3i
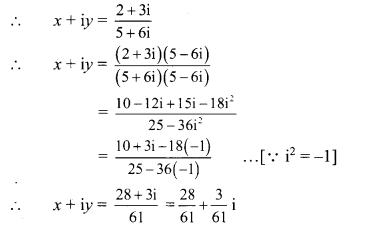
Equating real and imaginary parts, we get
x = \(\frac{28}{61}\) and y = \(\frac{3}{61}\)
(v) 2x + i
9
y (2 + i) = x i
7
+ 10 i
16
∴ 2x + (i
4
)
2
. i . y (2 + i) = x (i
2
)
3
. i + 10 . (i
4
)
4
∴ 2x + (1)
2
. iy (2 + i) = x (-1)
3
. i + 10 (1)
4
……[∵ i
2
= -1, i
4
= 1]
∴ 2x + 2yi + yi
2
= -xi + 10
∴ 2x + 2yi – y + xi = 10
∴ (2x – y) + (x + 2y)i = 10 + 0.i
Equating real and imaginary parts, we get
2x – y = 10 ……(i)
and x + 2y = 0 ……..(ii)
Equation (i) × 2 + equation (ii) gives
5x = 20
∴ x = 4
Putting x = 4 in (i), we get
2(4) – y = 10
∴ y = 8 – 10
∴ y = -2
∴ x = 4 and y = -2
Question 5.
Find the value of:
(i) x
3
+ 2x
2
– 3x + 21, if x = 1 + 2i
(ii) x
3
– 5x
2
+ 4x + 8, if x = \(\frac{10}{3-i}\)
(iii) x
3
– 3x
2
+ 19x – 20, if x = 1 – 4i
Solution:
(i) x = 1 + 2i
∴ x – 1 = 2i
∴ (x – 1)
2
= 4i
2
∴ x
2
– 2x + 1 = -4 ……[∵ i
2
= -1]
∴ x
2
– 2x + 5 = 0 ……(i)
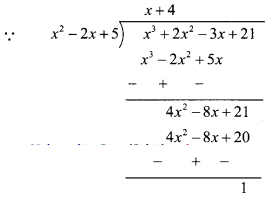
∴ x
3
+ 2x
2
– 3x + 21
= (x
2
– 2x + 5)(x + 4) + 1
= 0.(x + 4) + 1 ……[From (i)]
= 0 + 1
= 1
∴ x
3
+ 2x
2
– 3x + 21 = 1
(ii) x = \(\frac{10}{3-i}\)
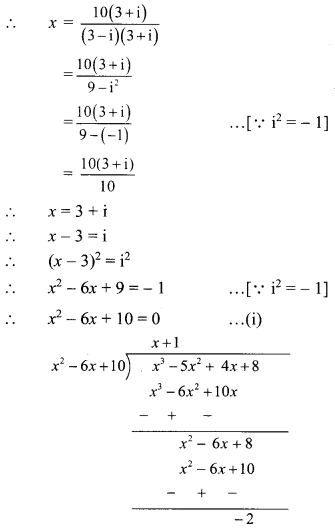
x
3
– 5x
2
+ 4x + 8
= (x
2
– 6x + 10)(x + 1) – 2
= 0 . (x + 1) – 2 ……[From (i)]
= 0 – 2
∴ x
3
– 5x
2
+ 4x + 8 = -2

(iii) x = 1 – 4i
∴ x – 1 = -4i
∴ (x – 1)
2
= 16i
2
∴ x
2
– 2x + 1 = -16 ……[∵ i
2
= -1]
∴ x
2
– 2x + 17 = 0 ……(i)
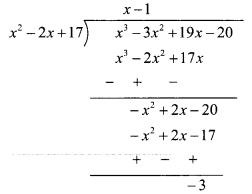
∴ x
3
– 3x
2
+ 19x – 20
= (x
2
– 2x + 17) (x – 1) – 3
= 0 . (x – 1) – 3 ….[From (i)]
= 0 – 3
= -3
∴ x
3
– 3x
2
+ 19x – 20 = -3
Question 6.
Find the square roots of:
(i) -16 + 30i
(ii) 15 – 8i
(iii) 2 + 2√3i
(iv) 18i
(v) 3 – 4i
(vi) 6 + 8i
Solution:
(i) Let \(\sqrt{-16+30 \mathrm{i}}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
-16 + 30i = a
2
+ b
2
i
2
+ 2abi
∴ -16 + 30i = (a
2
– b
2
) + 2abi …..[∵ i
2
= -1]
Equating real and imaginary parts, we get
a
2
– b
2
= -16 and 2ab = 30
∴ a
2
– b
2
= -16 and b = \(\frac{15}{a}\)
∴ a
2
– \(\left(\frac{15}{a}\right)^{2}\) = -16
∴ a
2
– \(\frac{225}{a^{2}}\) = -16
∴ a
4
– 225 = – 16a
2
∴ a
4
+ 16a
2
– 225 = 0
∴ (a
2
+ 25)(a
2
– 9) = 0
∴ a
2
= -25 or a
2
= 9
But a ∈ R, a
2
≠ -25
∴ a
2
= 9
∴ a = ±3
When a = 3, b = \(\frac{15}{3}\) = 5
When a = -3, b = \(\frac{15}{-3}\) = -5
∴ \(\sqrt{-16+30 \mathrm{i}}\) = ±(3 + 5i)
(ii) Let \(\sqrt{15-8 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
15 – 8i = a
2
+ b
2
i
2
+ 2abi
∴ 15 – 8i = (a
2
– b
2
) + 2abi ……[∵ i
2
= -1]
Equating real and imaginary parts, we get
a
2
– b
2
= 15 and 2ab = -8
∴ a
2
– b
2
= 15 and b = \(\frac{-4}{a}\)
∴ a
2
– (\(\left(\frac{-4}{a}\right)^{2}\)) = 15
∴ a
2
– \(\frac{16}{a^{2}}\) = 15
∴ a
4
– 16 = 15a
2
∴ a
4
– 15a
2
– 16 = 0
∴ (a
2
– 16)(a
2
+ 1) = 0
∴ a
2
= 16 or a
2
= -1
But a ∈ R, a
2
≠ -1
∴ a
2
= 16
∴ a = ±4
When a = 4, b = \(\frac{-4}{4}\) = -1
When a = -4, b = \(\frac{-4}{-4}\) = 1
\(\sqrt{15-8 i}\) = ±(4 – i)

(iii) Let \(\sqrt{2+2 \sqrt{3} i}\) = a + bi, where a, b ∈ R.
Squaring on both sides, we get
2 – 2√3i = a
2
+ b
2
i
2
+ 2abi
∴ 2 – 2√3i = a
2
– b
2
+ 2abi …..[∵ i
2
= -1]
Equating real and imaginary parts, we get
a
2
– b
2
= 2 and 2ab = 2√3
∴ a
2
– b
2
= 2 and b = \(\frac{\sqrt{3}}{\mathrm{a}}\)
∴ a
2
– \(\left(\frac{\sqrt{3}}{a}\right)^{2}\) = 2
∴ a
2
– \(\frac{3}{a^{2}}\) = 2
∴ a
4
– 3 = 2a
2
∴ a
4
– 2a
2
– 3 = 0
∴ (a
2
– 3)(a
2
+ 1) = 0
∴ a
2
= 3 or a
2
= -1
But a ∈ R, a
2
≠ -1
∴ a
2
= 3
∴ a = ±√3
When a = √3 , b = \(\frac{\sqrt{3}}{\sqrt{3}}\) = 1
When a = -√3 , b = \(\frac{\sqrt{3}}{-\sqrt{3}}\) = -1
∴ \(\sqrt{2+2 \sqrt{3} i}\) = ±(√3 + i)
(iv) Let \(\sqrt{18 \mathrm{i}}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
18i = a
2
+ b
2
i
2
+ 2abi
∴ 0 + 18i = a
2
– b
2
+ 2abi …..[∵ i
2
= -1]
Equating real and imaginary parts, we get
a
2
– b
2
= 0 and 2ab = 18
∴ a
2
– b
2
= 0 and b = \(\frac{9}{\mathrm{a}}\)
∴ a
2
– \(\left(\frac{9}{a}\right)^{2}\) = 0
∴ a
2
– \(\frac{81}{a^{2}}\) = 0
∴ a
4
– 81 = 0
∴ (a
2
– 9) (a
2
+ 9) = 0
∴ a
2
= 9 or a
2
= -9
But a ∈ R, a
2
≠ -9
∴ a
2
= 9
∴ a = ±3
When a = 3, b = \(\frac{9}{3}\) = 3
When a = 3, b = \(\frac{9}{-3}\) = -3
∴ \(\sqrt{18 \mathrm{i}}\) = ±3(1 + i)
(v) Let \(\sqrt{3-4 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
3 – 4i = a
2
+ b
2
i
2
+ 2abi
∴ 3 – 4i = a
2
– b
2
+ 2abi ……[∵ i
2
= -1]
Equating real and imaginary parts, we get
a
2
– b
2
= 3 and 2ab = -4
∴ a
2
– b
2
= 3 and b = \(\frac{-2}{a}\)
∴ a
2
– \(\left(-\frac{2}{a}\right)^{2}\) = 3
∴ a
2
– \(\frac{4}{a^{2}}\) = 3
∴ a
4
– 4 = 3a
2
∴ a
4
– 3a
2
– 4 = 0
∴ (a
2
– 4)(a
2
+ 1) = 0
∴ a
2
= 4 or a
2
= -1
But, a ∈ R, a
2
≠ -1
∴ a
2
= 4
∴ a = ±2
When a = 2, b = \(\frac{-2}{2}\) = -1
When a = -2, b = \(\frac{-2}{-2}\) = 1
∴ \(\sqrt{3-4 i}\) = ±(2 – i)

(vi) Let \(\sqrt{6+8 i}\) = a + bi, where a, b ∈ R
Squaring on both sides, we get
6 + 8i = a
2
+ b
2
i
2
+ 2abi
∴ 6 + 8i = a
2
– b
2
+ 2abi ……[∵ i
2
= -1]
Equating real and imaginary parts, we get
a
2
– b
2
= 6 and 2ab = 8
∴ a
2
– b
2
= 6 and b = \(\frac{4}{\mathrm{a}}\)
∴ a
2
– \(\left(\frac{4}{a}\right)^{2}\) = 6
∴ a
2
– \(\frac{16}{a^{2}}\) = 6
∴ a
4
– 16 = 6a
2
∴ a
4
– 6a
2
– 16 = 0
∴ (a
2
– 8)(a
2
+ 2) = 0
∴ a
2
= 8 or a
2
= -2
But a ∈ R, a
2
≠ -2
∴ a
2
= 8
∴ a = ±2√2
When a = 2√2, b = \(\frac{4}{2 \sqrt{2}}\) = √2
When a = -2√2, b = \(\frac{4}{-2 \sqrt{2}}\) = -√2
∴ \(\sqrt{6+8 i}\) = ±(2√2 + √2i) = ±√2(2 + i)