11th Commerce Maths 1 Chapter 4 Exercise 4.3 Answers Maharashtra Board

Sequences and Series Class 11 Commerce Maths 1 Chapter 4 Exercise 4.3 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 4 Sequences and Series Ex 4.3 Questions and Answers.

Std 11 Maths 1 Exercise 4.3 Solutions Commerce Maths

Question 1.
Determine whether the sum to infinity of the following G.P’.s exist. If exists, find it.
(i) \(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \ldots\)
(ii) \(2, \frac{4}{3}, \frac{8}{9}, \frac{16}{27}, \ldots\)
(iii) \(-3,1, \frac{-1}{3}, \frac{1}{9}, \ldots\)
(iv) \(\frac{1}{5}, \frac{-2}{5}, \frac{4}{5}, \frac{-8}{5}, \frac{16}{5}, \ldots\)
Solution:

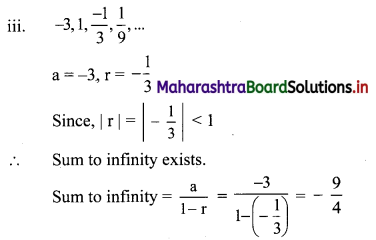
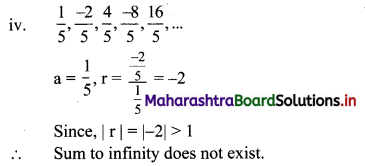
Question 2.
Express the following recurring decimals as a rational number.
(i) \(0 . \overline{32}\)
(ii) 3.5
(iii) \(4 . \overline{18}\)
(iv) \(0.3 \overline{45}\)
(v) \(3.4 \overline{56}\)
Solution:
(i) \(0 . \overline{32}\) = 0.323232…..
= 0.32 + 0.0032 + 0.000032 + …..
Here, 0.32, 0.0032, 0.000032, … are in G.P. with a = 0.32 and r = 0.01
Since, |r| = |0.01| < 1
∴ Sum to infinity exists.
∴ Sum to infinity = \(\frac{a}{1-r}\)

(ii) 3.5 = 3.555… = 3 + 0.5 + 0.05 + 0.005 + …
Here, 0.5, 0.05, 0.005, … are in G.P. with a = 0.5 and r = 0.1
Since, |r| = |0.1| < 1
∴ Sum to infinity exists.

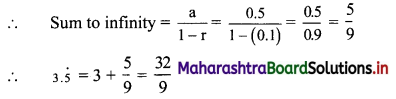
(iii) \(4 . \overline{18}\) = 4.181818…..
= 4 + 0.18 + 0.0018 + 0.000018 + …..
Here, 0.18, 0.0018, 0.000018, … are in G.P. with a = 0.18 and r = 0.01
Since, |r| = |0.01| < 1
∴ Sum to infinity exists.

(iv) 0.345 = 0.3454545…..
= 0.3 + 0.045 + 0.00045 + 0.0000045 + …..
Here, 0.045, 0.00045, 0.0000045, … are in G.P. with a = 0.045, r = 0.01
Since, |r| = |0.01| < 1
∴ Sum to infinity exists.

(v) \(3.4 \overline{56}\) = 3.4565656 …..
= 3.4 + 0.056 + 0.00056 + 0.0000056 + ….
Here, 0.056, 0.00056, 0.0000056, … are in G.P. with a = 0.056 and r = 0.01
Since, |r| = |0.01| < 1
∴ Sum to infinity exists.

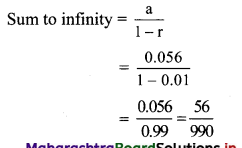
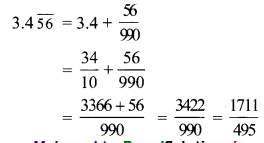
Question 3.
If the common ratio of a G.P. is \(\frac{2}{3}\) and sum of its terms to infinity is 12. Find the first term.
Solution:
r = \(\frac{2}{3}\), sum to infinity = 12 … [Given]
Sum to infinity = \(\frac{a}{1-r}\)
∴ 12 = \(\frac{a}{1-\frac{2}{3}}\)
∴ a = 12 × \(\frac{1}{3}\)
∴ a = 4

Question 4.
If the first term of a G.P. is 16 and sum of its terms to infinity is \(\frac{176}{5}\), find the common ratio.
Solution:
a = 16, sum to infinity = \(\frac{176}{5}\) … [Given]
Sum to infinity = \(\frac{a}{1-r}\)
∴ \(\frac{176}{5}=\frac{16}{1-r}\)
∴ \(\frac{11}{5}=\frac{1}{1-r}\)
∴ 11 – 11r = 5
∴ 11r = 6
∴ r = \(\frac{6}{11}\)

Question 5.
The sum of the terms of an infinite G.P. is 5 and the sum of the squares of those terms is 15. Find the G.P.
Solution:
Let the required G.P. be a, ar, ar ² , ar ³ , …..
Sum to infinity of this G.P. = 5
∴ 5 = \(\frac{a}{1-r}\)
∴ a = 5(1 – r) ……(i)
Also, the sum of the squares of the terms is 15.