11th Commerce Maths 2 Chapter 6 Exercise 6.6 Answers Maharashtra Board

Permutations and Combinations Class 11 Commerce Maths 2 Chapter 6 Exercise 6.6 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 6 Permutations and Combinations Ex 6.6 Questions and Answers.

Std 11 Maths 2 Exercise 6.6 Solutions Commerce Maths

Question 1.
Find the value of
(i) ¹⁵ C ₄
Solution:

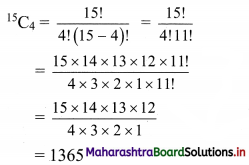
(ii) ⁸⁰ C ₂
Solution:

(iii) ¹⁵ C ₄ + ¹⁵ C ₅
Solution:

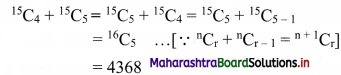
(iv) ²⁰ C ₁₆ – ¹⁹ C ₁₆
Solution:

Question 2.
Find n if
(i) ⁶ P ₂ = n ⁶ C ₂
Solution:

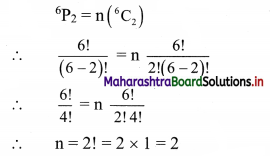
(ii) ²ⁿ C ₃ : ⁿ C ₂ = 52 : 3
Solution:

(iii) ⁿ C _n-3 = 84
Solution:
ⁿ C _n-3 = 84
∴ \(\frac{n !}{(n-3) ![n-(n-3)] !}\) = 84
∴ \(\frac{\mathrm{n}(\mathrm{n}-1)(\mathrm{n}-2)(\mathrm{n}-3) !}{(\mathrm{n}-3) ! \times 3 !}\) = 84
∴ n(n – 1) (n – 2) = 84 × 6
∴ n(n – 1) (n – 2) = 9 × 8 × 7
Comparing on both sides, we get
∴ n = 9

Question 3.
Find r if ¹⁴ C _2r : ¹⁰ C _2r-4 = 143 : 10
Solution:

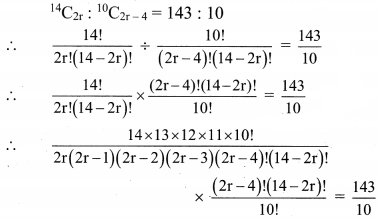
∴ \(\frac{14 \times 13 \times 12 \times 11}{2 \mathrm{r}(2 \mathrm{r}-1) \times(2 \mathrm{r}-2)(2 \mathrm{r}-3)}=\frac{143}{10}\)
∴ 2r(2r – 1)(2r – 2)(2r – 3) = 14 × 12 × 10
∴ 2r(2r – 1)(2r – 2)(2r – 3) = 8 × 7 × 6 × 5
Comparing on both sides, we get
∴ r = 4

Question 4.
Find n and r if.
(i) ⁿ P _r = 720 and ⁿ C _n-r = 120
Solution:

(ii) ⁿ C _r-1 : ⁿ C _r : ⁿ C _r+1 = 20 : 35 : 42
Solution:

Question 5.
If ⁿ P _r = 1814400 and ⁿ C _r = 45, find r.
Solution:

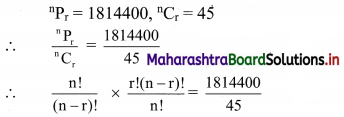
∴ r! = 40320
∴ r! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
∴ r! = 8!
∴ r = 8

Question 6.
If ⁿ C _r-1 = 6435, ⁿ C _r = 5005, ⁿ C _r+1 = 3003, find ^r C ₅ .
Solution:

Question 7.
Find the number of ways of drawing 9 balls from a bag that has 6 red balls, 5 green balls and 7 blue balls so that 3 balls of every colour are drawn.
Solution:
9 balls are to be selected from 6 red, 5 green, 7 blue balls such that the selection consists of 3 balls of each colour.
∴ 3 red balls can be selected from 6 red balls in ⁶ C ₃ ways.
3 green balls can be selected from 5 green balls in ⁵ C ₃ ways.
3 blue balls can be selected from 7 blue balls in ⁷ C ₃ ways.
∴ Number of ways selection can be done if the selection consists of 3 balls of each colour

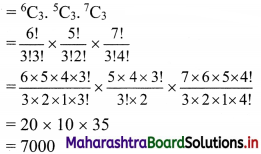
Question 8.
Find the number of ways of selecting a team of 3 boys and 2 girls from 6 boys and 4 girls.
Solution:
There are 6 boys and 4 girls.
A team of 3 boys and 2 girls is to be selected.
∴ 3 boys can be selected from 6 boys in ⁶ C ₃ ways.
2 girls can be selected from 4 girls in ⁴ C ₂ ways.
∴ Number of ways the team can be selected = ⁶ C ₃ × ⁴ C ₂
= \(\frac{6 !}{3 ! 3 !} \times \frac{4 !}{2 ! 2 !}\)
= \(\frac{6 \times 5 \times 4 \times 3 !}{3 \times 2 \times 1 \times 3 !} \times \frac{4 \times 3 \times 2 !}{2 \times 2 !}\)
= 20 × 6
= 120
∴ The team of 3 boys and 2 girls can be selected in 120 ways.

Question 9.
After a meeting, every participant shakes hands with every other participants. If the number of handshakes is 66, find the number of participants in the meeting.
Solution:
Let there be n participants present in the meeting.
A handshake occurs between 2 persons.
∴ Number of handshakes = ⁿ C ₂
Given 66 handshakes were exchanged.
∴ 66 = ⁿ C ₂
∴ 66 = \(\frac{n !}{2 !(n-2) !}\)
∴ 66 × 2 = \(\frac{\mathrm{n}(\mathrm{n}-1)(\mathrm{n}-2) !}{(\mathrm{n}-2) !}\)
∴ 132 = n(n – 1)
∴ n(n – 1) = 12 × 11
Comparing on both sides, we get n = 12
∴ 12 participants were present at the meeting.

Question 10.
If 20 points are marked on a circle, how many chords can be drawn?
Solution:
To draw a chord we need to join two points on the circle.
There are 20 points on a circle.
∴ Total number of chords possible from these points = ²⁰ C ₂
= \(\frac{20 !}{2 ! 18 !}\)
= \(\frac{20 \times 19 \times 18 !}{2 \times 1 \times 18 !}\)
= 190

Question 11.
Find the number of diagonals of an n-sided polygon. In particular, find the number of diagonals when
(i) n = 10
(ii) n = 15
(iii) n = 12
Solution:
In n-sided polygon, there are ‘n’ points and ‘n’ sides. .
∴ Through ‘n’ points we can draw ⁿ C ₂ lines including sides.
∴ Number of diagonals in n sided polygon = ⁿ C ₂ – n (∴ n = number of sides)

Question 12.
There are 20 straight lines in a plane so that no two lines are parallel and no three lines are concurrent. Determine the number of points of intersection.
Solution:
There are 20 lines such that no two of them are parallel and no three of them are concurrent.
Since no two lines are parallel
∴ they intersect at a point
∴ Number of points of intersection if no two lines are parallel and no three lines are concurrent = ²⁰ C ₂
= \(\frac{20 !}{2 ! 18 !}\)
= \(\frac{20 \times 19 \times 18 !}{2 \times 1 \times 18 !}\)
= 190

Question 13.
Ten points are plotted on a plane. Find the number of straight lines obtained by joining these points if
(i) no three points are collinear
(ii) four points are collinear
Solution:
There are 10 points on a plane.
(i) No three of them are collinear:
Since a line is obtained by joining 2 points,
number of lines passing through these points if no three points are collinear = ¹⁰ C ₂
= \(\frac{10 !}{2 ! 8 !}\)
= \(\frac{10 \times 9 \times 8 !}{2 \times 1 \times 8 !}\)
= 5 × 9
= 45

(ii) When 4 of them arc collinear:
∴ Number of lines passing through these points if 4 points are collinear
= ¹⁰ C ₂ – ⁴ C ₂ + 1
= 45 – \(\frac{4 !}{2 ! 2 !}\) + 1
= 45 – \(\frac{4 \times 3 \times 2 !}{2 \times 2 !}\) + 1
= 45 – 6 + 1
= 40

Question 14.
Find the number of triangles formed by joining 12 points if
(i) no three points are collinear
(ii) four points are collinear
Solution:
There are 12 points on the plane
(i) When no three of them are collinear:
Since a triangle can be drawn by joining any three non-collinear points.
∴ Number of triangles that can be obtained from these points = ¹² C ₃
= \(\frac{12 !}{3 ! 9 !}\)
= \(\frac{12 \times 11 \times 10 \times 9 !}{3 \times 2 \times 1 \times 9 !}\)
= 220

(ii) When 4 of these points are collinear:
∴ Number of triangles that can be obtained from these points = ¹² C ₃ – ⁴ C ₃
= 220 – \(\frac{4 !}{3 ! \times 1 !}\)
= 220 – \(\frac{4 \times 3 !}{3 !}\)
= 220 – 4
= 216

Question 15.
A word has 8 consonants and 3 vowels. How many distinct words can be formed if 4 consonants and 2 vowels are chosen?
Solution:
Out of 8 consonants, 4 can be selected in ⁸ C ₄
= \(\frac{8 !}{4 ! 4 !}\)
= \(\frac{8 \times 7 \times 6 \times 5 \times 4 !}{4 \times 3 \times 2 \times 1 \times 4 !}\)
= 70 ways
From 3 vowels, 2 can be selected in ³ C ₂
= \(\frac{3 !}{2 ! 1 !}\)
= \(\frac{3 \times 2 !}{2 !}\)
= 3 ways
Now, to form a word, these 6 letters (i.e., 4 consonants and 2 vowels) can be arranged in ⁶ P ₆ i.e., 6! ways.
∴ Total number of words that can be formed = 70 × 3 × 6!
= 70 × 3 × 720
= 151200
∴ 151200 words of 4 consonants and 2 vowels can be formed.