Permutations and Combinations Class 11 Commerce Maths 2 Chapter 6 Exercise 6.6 Answers Maharashtra Board
Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 6 Permutations and Combinations Ex 6.6 Questions and Answers.
Std 11 Maths 2 Exercise 6.6 Solutions Commerce Maths
Question 1.
Find the value of
(i)
15
C
4
Solution:
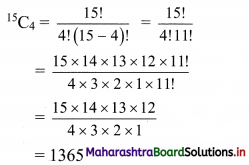
(ii)
80
C
2
Solution:

(iii)
15
C
4
+
15
C
5
Solution:
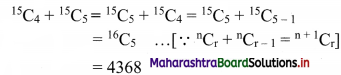
(iv)
20
C
16
–
19
C
16
Solution:

Question 2.
Find n if
(i)
6
P
2
= n
6
C
2
Solution:
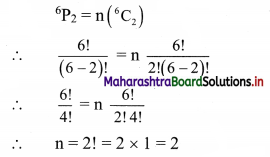
(ii)
2n
C
3
:
n
C
2
= 52 : 3
Solution:

(iii)
n
C
n-3
= 84
Solution:
n
C
n-3
= 84
∴ n!(n−3)![n−(n−3)]! = 84
∴ n(n−1)(n−2)(n−3)!(n−3)!×3! = 84
∴ n(n – 1) (n – 2) = 84 × 6
∴ n(n – 1) (n – 2) = 9 × 8 × 7
Comparing on both sides, we get
∴ n = 9

Question 3.
Find r if
14
C
2r
:
10
C
2r-4
= 143 : 10
Solution:
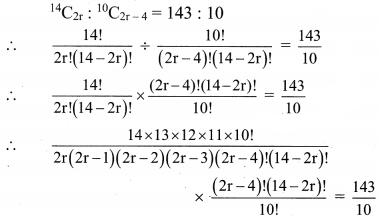
∴ 14×13×12×112r(2r−1)×(2r−2)(2r−3)=14310
∴ 2r(2r – 1)(2r – 2)(2r – 3) = 14 × 12 × 10
∴ 2r(2r – 1)(2r – 2)(2r – 3) = 8 × 7 × 6 × 5
Comparing on both sides, we get
∴ r = 4
Question 4.
Find n and r if.
(i)
n
P
r
= 720 and
n
C
n-r
= 120
Solution:

(ii)
n
C
r-1
:
n
C
r
:
n
C
r+1
= 20 : 35 : 42
Solution:


Question 5.
If
n
P
r
= 1814400 and
n
C
r
= 45, find r.
Solution:
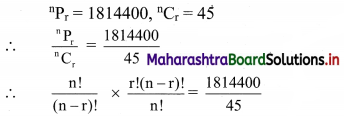
∴ r! = 40320
∴ r! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
∴ r! = 8!
∴ r = 8
Question 6.
If
n
C
r-1
= 6435,
n
C
r
= 5005,
n
C
r+1
= 3003, find
r
C
5
.
Solution:


Question 7.
Find the number of ways of drawing 9 balls from a bag that has 6 red balls, 5 green balls and 7 blue balls so that 3 balls of every colour are drawn.
Solution:
9 balls are to be selected from 6 red, 5 green, 7 blue balls such that the selection consists of 3 balls of each colour.
∴ 3 red balls can be selected from 6 red balls in
6
C
3
ways.
3 green balls can be selected from 5 green balls in
5
C
3
ways.
3 blue balls can be selected from 7 blue balls in
7
C
3
ways.
∴ Number of ways selection can be done if the selection consists of 3 balls of each colour
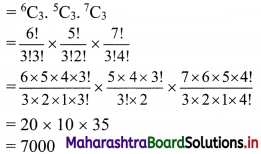
Question 8.
Find the number of ways of selecting a team of 3 boys and 2 girls from 6 boys and 4 girls.
Solution:
There are 6 boys and 4 girls.
A team of 3 boys and 2 girls is to be selected.
∴ 3 boys can be selected from 6 boys in
6
C
3
ways.
2 girls can be selected from 4 girls in
4
C
2
ways.
∴ Number of ways the team can be selected =
6
C
3
×
4
C
2
= 6!3!3!×4!2!2!
= 6×5×4×3!3×2×1×3!×4×3×2!2×2!
= 20 × 6
= 120
∴ The team of 3 boys and 2 girls can be selected in 120 ways.

Question 9.
After a meeting, every participant shakes hands with every other participants. If the number of handshakes is 66, find the number of participants in the meeting.
Solution:
Let there be n participants present in the meeting.
A handshake occurs between 2 persons.
∴ Number of handshakes =
n
C
2
Given 66 handshakes were exchanged.
∴ 66 =
n
C
2
∴ 66 = n!2!(n−2)!
∴ 66 × 2 = n(n−1)(n−2)!(n−2)!
∴ 132 = n(n – 1)
∴ n(n – 1) = 12 × 11
Comparing on both sides, we get n = 12
∴ 12 participants were present at the meeting.
Question 10.
If 20 points are marked on a circle, how many chords can be drawn?
Solution:
To draw a chord we need to join two points on the circle.
There are 20 points on a circle.
∴ Total number of chords possible from these points =
20
C
2
= 20!2!18!
= 20×19×18!2×1×18!
= 190
Question 11.
Find the number of diagonals of an n-sided polygon. In particular, find the number of diagonals when
(i) n = 10
(ii) n = 15
(iii) n = 12
Solution:
In n-sided polygon, there are ‘n’ points and ‘n’ sides. .
∴ Through ‘n’ points we can draw
n
C
2
lines including sides.
∴ Number of diagonals in n sided polygon =
n
C
2
– n (∴ n = number of sides)

Question 12.
There are 20 straight lines in a plane so that no two lines are parallel and no three lines are concurrent. Determine the number of points of intersection.
Solution:
There are 20 lines such that no two of them are parallel and no three of them are concurrent.
Since no two lines are parallel
∴ they intersect at a point
∴ Number of points of intersection if no two lines are parallel and no three lines are concurrent =
20
C
2
= 20!2!18!
= 20×19×18!2×1×18!
= 190

Question 13.
Ten points are plotted on a plane. Find the number of straight lines obtained by joining these points if
(i) no three points are collinear
(ii) four points are collinear
Solution:
There are 10 points on a plane.
(i) No three of them are collinear:
Since a line is obtained by joining 2 points,
number of lines passing through these points if no three points are collinear =
10
C
2
= 10!2!8!
= 10×9×8!2×1×8!
= 5 × 9
= 45
(ii) When 4 of them arc collinear:
∴ Number of lines passing through these points if 4 points are collinear
=
10
C
2
–
4
C
2
+ 1
= 45 – 4!2!2! + 1
= 45 – 4×3×2!2×2! + 1
= 45 – 6 + 1
= 40
Question 14.
Find the number of triangles formed by joining 12 points if
(i) no three points are collinear
(ii) four points are collinear
Solution:
There are 12 points on the plane
(i) When no three of them are collinear:
Since a triangle can be drawn by joining any three non-collinear points.
∴ Number of triangles that can be obtained from these points =
12
C
3
= 12!3!9!
= 12×11×10×9!3×2×1×9!
= 220
(ii) When 4 of these points are collinear:
∴ Number of triangles that can be obtained from these points =
12
C
3
–
4
C
3
= 220 – 4!3!×1!
= 220 – 4×3!3!
= 220 – 4
= 216

Question 15.
A word has 8 consonants and 3 vowels. How many distinct words can be formed if 4 consonants and 2 vowels are chosen?
Solution:
Out of 8 consonants, 4 can be selected in
8
C
4
= 8!4!4!
= 8×7×6×5×4!4×3×2×1×4!
= 70 ways
From 3 vowels, 2 can be selected in
3
C
2
= 3!2!1!
= 3×2!2!
= 3 ways
Now, to form a word, these 6 letters (i.e., 4 consonants and 2 vowels) can be arranged in
6
P
6
i.e., 6! ways.
∴ Total number of words that can be formed = 70 × 3 × 6!
= 70 × 3 × 720
= 151200
∴ 151200 words of 4 consonants and 2 vowels can be formed.