11th Commerce Maths 1 Chapter 8 Miscellaneous Exercise 8 Answers Maharashtra Board

Continuity Class 11 Commerce Maths 1 Chapter 8 Miscellaneous Exercise 8 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 8 Continuity Miscellaneous Exercise 8 Questions and Answers.

Std 11 Maths 1 Miscellaneous Exercise 8 Solutions Commerce Maths

I. Discuss the continuity of the following functions at the point(s) or in the interval indicated against them.

Question 1.
If f(x) = 2x ² – 2x + 5 for 0 ≤ x < 2
= \(\frac{1-3 x-x^{2}}{1-x}\) for 2 ≤ x < 4
= \(\frac{7-x^{2}}{x-5}\) for 4 ≤ x ≤ 7 on its domain.
Solution:
The domain of f is [0, 5) ∪ (5, 7]
We observe that x = 5 is not included in the domain as f is not defined at x = 5
a. For 0 ≤ x < 2
f(x) = 2x ² – 2x + 5
It is a polynomial function and is continuous at all point in [0, 2)

b. For 2 < x < 4
f(x) = \(\frac{1-3 x-x^{2}}{1-x}\)
It is a rational function and is continuous everwhere except at points where its denominator becomes zero.
Denominator becomes zero at x = 1
But x = 1 does not lie in the interval.
f(x) is continuous at all points in (2, 4)

c. For 4 < x ≤ 7, x ≠ 5
i.e. for x ∈ [4, 5) ∪ (5, 7]
∴ f(x) = \(\frac{7-x^{2}}{x-5}\)
It is a rational function and is continuous everywhere except possibly at points where its denominator becomes zero.
Denominator becomes zero at x = 5
But x = 5 ∉ [4, 5) ∪ (5, 7]
∴ f is continuous at all points in (4, 7] – {5}.

d. Since the definition of function changes around x = 2, x = 4 and x = 7
∴ there is disturbance in behaviour of the function.
So we examine continuity at x = 2, 4, 7 separately.
Continuity at x = 2:
\(\lim _{x \rightarrow 2^{-}} f(x)=\lim _{x \rightarrow 2^{-}}\left(2 x^{2}-2 x+5\right)\)
= 2(2) ² – 2(2) + 5
= 8 – 4 + 5
= 9

∴ f is continuous at x = 2

e. Continuity at x = 4:

∴ f is continuous at x = 4

Question 2.
f(x) = \(\frac{3^{x}+3^{-x}-2}{x^{2}}\) for x ≠ 0
= (log 3) ² for x = 0 at x = 0
Solution:


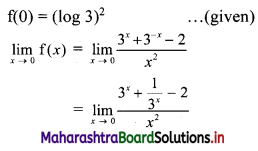
∴ \(\lim _{x \rightarrow 0} f(x)=f(0)\)
∴ f is continuous at x = 0

Question 3.
f(x) = \(\frac{5^{x}-e^{x}}{2 x}\) for x ≠ 0
= \(\frac{1}{2}\) (log 5 – 1) for x = 0 at x = 0
Solution:

∴ \(\lim _{x \rightarrow 0} f(x)=f(0)\)
∴ f is continuous at x = 0

Question 4.
f(x) = \(\frac{\sqrt{x+3}-2}{x^{3}-1}\) for x ≠ 1
= 2 for x = 1, at x = 1
Solution:


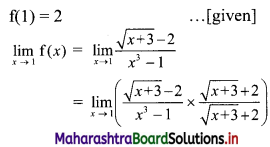
∴ \(\lim _{x \rightarrow 1} \mathrm{f}(x) \neq \mathrm{f}(1)\)
∴ f is discontinuous at x = 1

Question 5.
f(x) = \(\frac{\log x-\log 3}{x-3}\) for x ≠ 3
= 3 for x = 3, at x = 3
Solution:

(II) Find k if following functions are continuous at the points indicated against them.

Question 1.
f(x) = \(\left(\frac{5 x-8}{8-3 x}\right)^{\frac{3}{2 x-4}}\) for x ≠ 2
= k for x = 2 at x = 2
Solution:

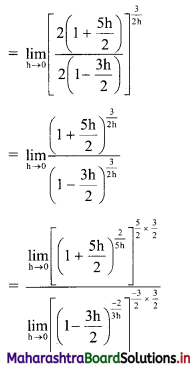
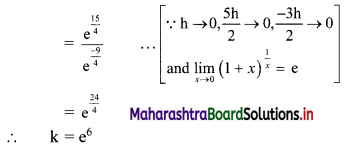
Question 2.
f(x) = \(\frac{45^{x}-9^{x}-5^{x}+1}{\left(k^{x}-1\right)\left(3^{x}-1\right)}\) for x ≠ 0
= \(\frac{2}{3}\) for x = 0, at x = 0
Solution:

Question 3.
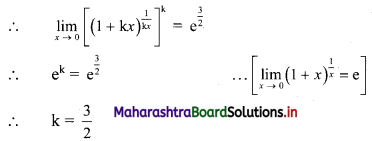
f(x) = \((1+k x)^{\frac{1}{x}}\), for x ≠ 0
= \(e^{\frac{3}{2}}\), for x = 0, at x = 0
Solution:

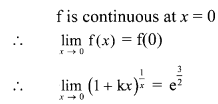
III. Find a and b if following functions are continuous at the point indicated against them.

Question 1.
f(x) = x ² + a, for x ≥ 0
= 2\(\sqrt{x^{2}+1}\) + b, for x < 0 and
f(1) = 2, is continuous at x = 0
Solution:

Question 2.
f(x) = \(\frac{x^{2}-9}{x-3}\) + a, for x > 3
= 5, for x = 3
= 2x ² + 3x + b, for x < 3
is continuous at x = 3
Solution:

Question 3.
f(x) = \(\frac{32^{x}-1}{8^{x}-1}\) + a, for x > 0
= 2, for x = 0
= x + 5 – 2b, for x < 0
is continuous at x = 0
Solution: