11th Commerce Maths 1 Chapter 9 Exercise 9.2 Answers Maharashtra Board

Differentiation Class 11 Commerce Maths 1 Chapter 9 Exercise 9.2 Answers Maharashtra Board

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Differentiation Ex 9.2 Questions and Answers.

Std 11 Maths 1 Exercise 9.2 Solutions Commerce Maths

I. Differentiate the following functions w.r.t. x.

Question 1.
\(\frac{x}{x+1}\)
Solution:

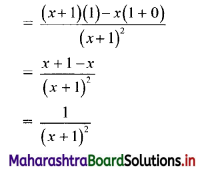
Question 2.
\(\frac{x^{2}+1}{x}\)
Solution:

Question 3.
\(\frac{1}{e^{x}+1}\)
Solution:

Question 4.
\(\frac{e^{x}}{e^{x}+1}\)
Solution:

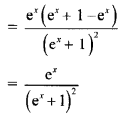
Question 5.
\(\frac{x}{\log x}\)
Solution:

Question 6.
\(\frac{2^{x}}{\log x}\)
Solution:

Question 7.
\(\frac{\left(2 e^{x}-1\right)}{\left(2 e^{x}+1\right)}\)
Solution:

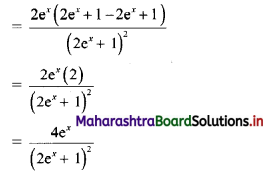
Question 8.
\(\frac{(x+1)(x-1)}{\left(e^{x}+1\right)}\)
Solution:

II. Solve the following examples:

Question 1.
The demand D for a price P is given as D = \(\frac{27}{P}\), find the rate of change of demand when the price is 3.
Solution:
Demand, D = \(\frac{27}{P}\)
Rate of change of demand = \(\frac{dD}{dP}\)

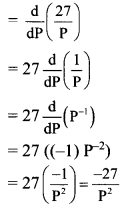
When price P = 3,
Rate of change of demand,
\(\left(\frac{\mathrm{dD}}{\mathrm{dP}}\right)_{\mathrm{P}=3}=\frac{-27}{(3)^{2}}=-3\)
∴ When price is 3, Rate of change of demand is -3.

Question 2.
If for a commodity; the price-demand relation is given as D = \(\frac{P+5}{P-1}\). Find the marginal demand when the price is 2.
Solution:

Question 3.
The demand function of a commodity is given as P = 20 + D – D ² . Find the rate at which price is changing when demand is 3.
Solution:
Given, P = 20 + D – D ²
Rate of change of price = \(\frac{dP}{dD}\)
= \(\frac{d}{dD}\)(20 + D – D ² )
= 0 + 1 – 2D
= 1 – 2D
Rate of change of price at D = 3 is
\(\left(\frac{\mathrm{dP}}{\mathrm{dD}}\right)_{\mathrm{D}=3}\) = 1 – 2(3) = -5
∴ Price is changing at a rate of -5, when demand is 3.

Question 4.
If the total cost function is given by; C = 5x ³ + 7x ² + 7; find the average cost and the marginal cost when x = 4.
Solution:
Total cost function, C = 5x ³ + 7x ² + 7
Average cost = \(\frac{C}{x}\)

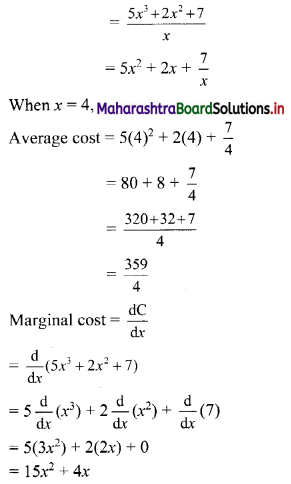
When x = 4, Marginal cost = \(\left(\frac{\mathrm{dC}}{\mathrm{d} x}\right)_{x=4}\)
= 15(4) ² + 4(4)
= 240 + 16
= 256
∴ the average cost and marginal cost at x = 4 are \(\frac{359}{4}\) and 256 respectively.

Question 5.
The total cost function of producing n notebooks is given by
C = 1500 – 75n + 2n ² + \(\frac{n^{3}}{5}\)
Find the marginal cost at n = 10.
Solution:
The total cost function,


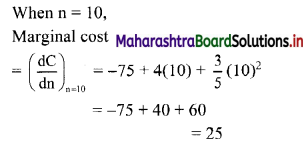
∴ Marginal cost at n = 10 is 25.

Question 6.
The total cost of ‘t’ toy cars is given by C = 5(2t) + 17. Find the marginal cost and average cost at t = 3.
Solution:
Total cost of ‘t’ toy cars, C = 5(2t) + 17

∴ at t = 3, the Marginal cost is 40 log 2 and the Average cost is 19.

Question 7.
If for a commodity; the demand function is given by, D = \(\sqrt{75-3 P}\). Find the marginal demand function when P = 5.
Solution:
Demand function, D = \(\sqrt{75-3 P}\)
Now, Marginal demand = \(\frac{dD}{dP}\)

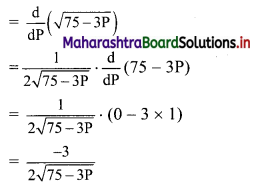
Question 8.
The total cost of producing x units is given by C = 10e ^2x , find its marginal cost and average cost when x = 2.
Solution:

Question 9.
The demand function is given as P = 175 + 9D + 25D ² . Find the revenue, average revenue, and marginal revenue when demand is 10.
Solution:
Given, P = 175 + 9D + 25D ²
Total revenue, R = P.D
= (175 + 9D + 25D ² )D
= 175D + 9D ² + 25D ³
Average revenue = P = 175 + 9D + 25D ²
Marginal revenue = \(\frac{dR}{dD}\)
= \(\frac{d}{dD}\) (175D + 9D ² + 25D ³ )
= 175 \(\frac{d}{dD}\) (D) + 9 \(\frac{d}{dD}\) (D ² ) + 25 \(\frac{d}{dD}\) (D ³ )
= 175(1) + 9(2D) + 25(3D ² )
= 175 + 18D + 75D ²
When D = 10,
Total revenue = 175(10) + 9(10) ² + 25(10) ³
= 1750 + 900 + 25000
= 27650
Average revenue = 175 + 9(10) + 25(10) ²
= 175 + 90 + 2500
= 2765
Marginal revenue = 175 + 18(10) + 75(10) ²
= 175 + 180 + 7500
= 7855
∴ When Demand = 10,
Total revenue = 27650, Average revenue = 2765, Marginal revenue = 7855.

Question 10.
The supply S for a commodity at price P is given by S = P ² + 9P – 2. Find the marginal supply when the price is 7.
Solution:
Given, S = P ² + 9P – 2

∴ The marginal supply is 23, at P = 7.

Question 11.
The cost of producing x articles is given by C = x ² + 15x + 81. Find the average cost and marginal cost functions. Find marginal cost when x = 10. Find x for which the marginal cost equals the average cost.
Solution:
Given, cost C = x ² + 15x + 81

If marginal cost = average cost, then
2x + 15 = x + 15 + \(\frac{81}{x}\)
∴ x = \(\frac{81}{x}\)
∴ x ² = 81
∴ x = 9 …..[∵ x > 0]