12th Commerce Maths 2 Chapter 2 Exercise 2.2 Answers Maharashtra Board

Insurance and Annuity Class 12 Commerce Maths 2 Chapter 2 Exercise 2.2 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 2 Insurance and Annuity Ex 2.2 Questions and Answers.

Std 12 Maths 2 Exercise 2.2 Solutions Commerce Maths

Question 1.
Find the accumulated (future) value of annuity of ₹ 800 for 3 year at interest rate 8% compounded annually. [Given: (1.08) ³ = 1.2597]
Solution:
∵ C = ₹ 800
∵ n = 3 years
∵ r = 8% p.a.

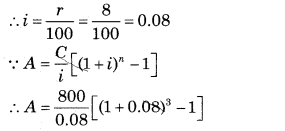
∴ A = 10,000[(1.08) ³ – 1]
∴ A = 10,000[1.2597 – 1]
∴ A = 10,000 × 0.2597
∴ A = ₹ 2,597

Question 2.
A person invested ₹ 5,000 every year in finance company that offered him interest compounded at 10% p.a., what is the amount accumulated after 4 years? [Given: (1.1) ⁴ = 1.4641]
Solution:
∵ C = ₹ 5,000
∵ r = 10% p.a.

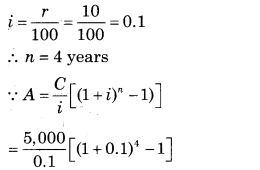
= 50,000[(1.1) ⁴ – 1]
= 50,000[1.4641 – 1]
= 50,000 × 0.4641
= ₹ 23,205

Question 3.
Find the amount accumulated after 2 years if a sum of ₹ 24,000 is invested every six months at 12% p.a. compounded half yearly. [Given: (1.06) ⁴ = 1.2625]
Solution:
∵ C = ₹ 24,000
∵ n = 2 years
But invested half yearly
∴ n = 2 × 2 = 4
∵ r = 12% p.a. compounded half yearly

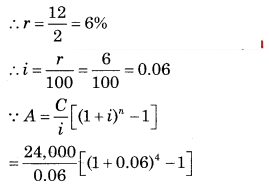
= 4,00,000[(1.06) ⁴ – 1]
= 4,00,000[1.2625 – 1]
= 4,00,000 × 0.2625
= ₹ 1,05,000

Question 4.
Find the accumulated value after 1 year of an annuity immediate in which ₹ 10,000 are invested every quarter at 16% p.a. compounded quarterly. [Given: (1.04) ⁴ = 1.1699]
Solution:
∵ C = ₹ 10,000
∵ n = 1 year
But invested every quarterly
∴ n = 1 × 4 = 4
∴ r = 16% p.a. compounded quarterly

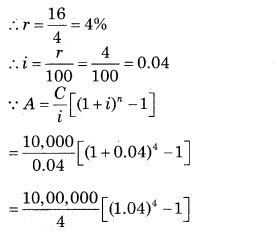
= 2,50,000 [1.1699 – 1]
= 2,50,000 × 0.1699
= ₹ 42,475

Question 5.
Find the present value of an annuity immediate of ₹ 36,000 p.a. for 3 years at 9% p.a. compounded annually. [Given: (1.09) ^-3 = 0.7722]
Solution:
∵ C = ₹ 36,000
∵ n = 3 years
∵ r = 9% p.a.

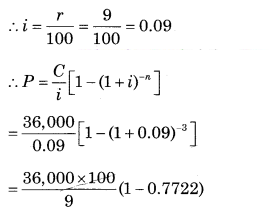
= 4,00,000 × 0.2278
= ₹ 91,120

Question 6.
Find the present value of ordinary annuity of ₹ 63,000 p.a. for 4 years at 14% p.a. compounded annually. [Given: (1.14) ^-4 = 0.5921]
Solution:
∵ C = ₹ 63,000
∵ n = 4 years
∵ r = 14% p.a.

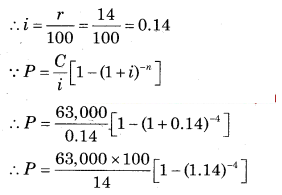
= 4,50,000[1 – 0.5921]
= 4,50,000 × 0.4079
= ₹ 1,83,555

Question 7.
A lady plans to save for her daughter’s marriage. She wishes to accumulate a sum of ₹ 4,64,100 at the end of 4 years. What amount should she invest every year if she get an interest of 10%p.a. compounded annually? [Given: (1.1) ⁴ = 1.4641]
Solution:
∵ A = ₹ 4,64,100
∵ n = 4 years
∵ r = 10% p.a.

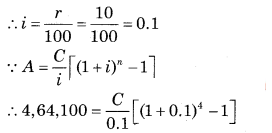
∴ 46,410 = C[1.4641 – 1]
∴ 46,410 = C × 0.4641
∴ \(\frac{46,410}{0.4641}\) = C
∴ C = ₹ 1,00,000

Question 8.
A person wants to create a fund of ₹ 6,96,150 after 4 years at the time of his retirement. He decides to invest a fixed amount at the end of every year in a bank that offers him interest of 10% p.a. compounded annually. What amount should he invest every year? [Given: (1.1) ⁴ = 1.4641]
Solution:
∵ A = ₹ 6,96,150
∵ n = 4 years
∵ r = 10% p.a

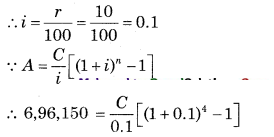
∴ 69,615 = C[1.4641 – 1]
∴ 69,615 = C × 0.4641
∴ \(\frac{69,615}{0.4641}\) = C
∴ C = ₹ 1,50,000

Question 9.
Find the rate of interest compounded annually if an annuity immediate at ₹ 20,000 per year amounts to ₹ 2,60,000 in 3 years.
Solution:
∵ C = ₹ 20,000
∵ A = ₹ 2,60,000
∵ n = 3 years

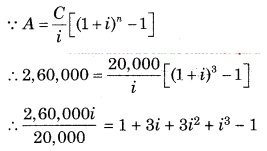
∴ 13i = 3i + 3 i ² + i ³
∴ 13i = i(3 + 3i + i ² )
∴ 13 = 3 + i + i ²
∴ i ² + 3i + 3 – 13 = 0
∴ i ² + 3i – 10 = 0
∴ (i + 5) (i – 2) = 0
∴ i + 5 = 0 or i – 2 = 0
∴ i = -5 or i = 2
∵ Rate of interest cannot be negative
∴ i = 2 is accepted
∴ \(\frac{r}{100}\) = 2
∴ r = 200% p.a.

Question 10.
Find the number of years for which an annuity of ₹ 500 is paid at the end of every years, if the accumulated amount works out to be ₹ 1,655 when interest is compounded annually at 10% p.a.
Solution:
∵ C = 7500
∵ A = 71,655
∵ r = 10% p.a.


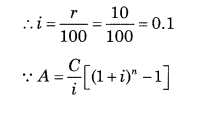
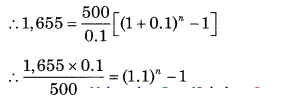
∴ 0.331 + 1 = (1.1) ⁿ
∴ 1.331 = (1.1) ⁿ
∴ (1.1) ³ = (1.1) ⁿ
∴ n = 3 years

Question 11.
Find the accumulated value of annuity due of ₹ 1,000 p.a. for 3 years at 10% p.a. compounded annually. [Given: (1.1) ³ = 1.331]
Solution:
∵ C = ₹ 1,000
∵ n = 3 years
∵ r = 10% p.a.

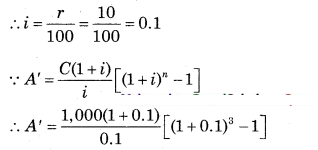
∴ A’ = 10,000 × 1.1[(1.1) ³ – 1]
∴ A’ = 11,000 [1.331 – 1]
∴ A’ = 11,000 × 0.331
∴ A’ = ₹ 3,641

Question 12.
A person plans to put ₹ 400 at the beginning of each year for 2 years in a deposit that gives interest at 2% p.a. compounded annually. Find the amount that will be accumulated at the end of 2 years. [Given: (1.02) ² = 1.0404]
Solution:
∵ C = ₹ 400
∵ r = 2% p.a.


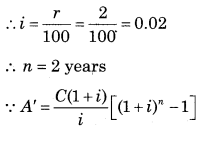
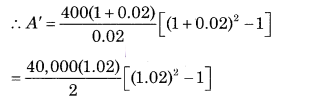
= 20,000 (1.02) (1.0404 – 1)
= 20,400 [0.0404]
= ₹ 824.16

Question 13.
Find the present value of an annuity due of ₹ 600 to be paid quarterly at 32% p.a. compounded quarterly. [Given (1.08) ^-4 = 0.7350]
Solution:
∵ C = ₹ 600
∵ n = 1 year
∴ But invested every quarterly
∴ n = 1 × 4 = 4
∵ r = 32% p.a. compounded quarterly

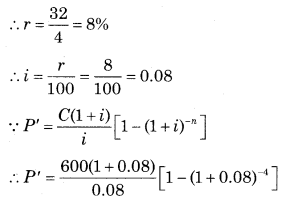
= 7,500(1.08) [1 – 0.7350]
= 8,100 [0.2650]
= ₹ 2,146.5

Question 14.
An annuity immediate is to be paid for some years at 12% p.a. The present value of the annuity is ₹ 10,000 and the accumulated value is ₹ 20,000. Find the amount of each annuity payment.
Solution:
∵ r = 12% p.a.
∴ i = \(\frac{r}{100}=\frac{12}{100}\) = 0.12
∵ P = ₹ 10,000
∵ A = ₹ 20,000
∵ \(\frac{1}{P}-\frac{1}{A}=\frac{i}{C}\)

∴ C = 0.12 × 20,000
∴ C = ₹ 2,400

Question 15.
For an annuity immediate paid for 3 years with interest compounded at 10% p.a. the present value is ₹ 24,000. What will be the accumulated value after 3 years? [Given (1.1) ³ = 1.331]
Solution:
∵ n = 3 years
∵ P = ₹ 24,000
∵ r = 10% p.a.
∴ i = \(\frac{r}{100}=\frac{10}{100}\) = 0.1
∵ A = P(1 + i) ⁿ
∴ A = 24,000 [1 + 0.1] ³
∴ A = 24,000 × (1.1) ³
∴ A = 24,000 × 1.331
∴ A = ₹ 31,944

Question 16.
A person sets up a sinking fund in order to have ₹ 1,00,000 after 10 years. What amount should be deposited bi-annually in the account that pays him 5% p.a. compounded semi-annually? [Given: (1.025) ²⁰ = 1.675]
Solution:
∴ A = ₹ 1,00,000
∴ n = 10 years
But, invested half yearly
∴ n = 10 × 2 = 20
∵ r = 5% p.a. compounded half yearly
∴ r = \(\frac{r}{2}=\frac{5}{2}\) = 2.5%
∴ i = \(\frac{r}{100}=\frac{2.5}{100}\) = 0.025

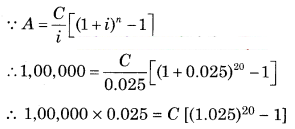
∴ 2,500 = C[1.675 – 1]
∴ 2,500 = C × 0.675
∴ \(\frac{2,500}{0.675}\) = C
∴ C = ₹ 3,703.70