12th Commerce Maths 2 Chapter 2 Miscellaneous Exercise 2 Answers Maharashtra Board

Insurance and Annuity Class 12 Commerce Maths 2 Chapter 2 Miscellaneous Exercise 2 Answers Maharashtra Board

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 2 Insurance and Annuity Miscellaneous Exercise 2 Questions and Answers.

Std 12 Maths 2 Miscellaneous Exercise 2 Solutions Commerce Maths

(I) Choose the correct alternative.

Question 1.
“A contract that pledges payment of an agreed-upon amount to the person (or his/her nominee) on the happening of an event covered against” is technically known as
(a) Death coverage
(b) Saving for future
(c) Life insurance
(d) Provident fund
Answer:
(c) Life insurance

Question 2.
Insurance companies collect a fixed amount from their customers at a fixed interval of time. This amount is called
(a) EMI
(b) Installment
(c) Contribution
(d) Premium
Answer:
(d) Premium

Question 3.
Following are different types of insurance.
I. Life insurance
II. Health insurance
III. Liability insurance
(a) Only I
(b) Only II
(c) Only III
(d) All the three
Answer:
(d) All the three

Question 4.
By taking insurance, an individual
(a) Reduces the risk of an accident
(b) Reduces the cost of an accident
(c) Transfers the risk to someone else
(d) Converts the possibility of large loss to the certainty of a small one
Answer:
Converts the possibility of large loss to the certainty of a small one

Question 5.
You get payments of ₹ 8,000 at the beginning of each year for five years ta 6%, what is the value of this annuity?
(a) ₹ 34,720
(b) ₹ 39,320
(c) ₹ 35,720
(d) ₹ 40,000
Answer:
(c) ₹ 35,720

Question 6.
In an ordinary annuity, payments or receipts occur at
(a) Beginning of each period
(b) End of each period
(c) Mid of each period
(d) Quarterly basis
Answer:
(b) End of each period

Question 7.
The amount of money today which is equal to a series of payments in the future is called
(a) Normal value of the annuity
(b) Sinking value of the annuity
(c) Present value of the annuity
(d) Future value of the annuity
Answer:
(c) Present value of the annuity

Question 8.
Rental payment for an apartment is an example of
(a) Annuity due
(b) Perpetuity
(c) Ordinary annuity
(d) Installment
Answer:
(b) Perpetuity

Question 9.
_________ is a series of constant cash flows over a limited period of time.
(a) Perpetuity
(b) Annuity
(c) Present value
(d) Future value
Answer:
(b) Annuity

Question 10.
A retirement annuity is particularly attractive to someone who has
(a) A severe illness
(b) Risk of low longevity
(c) Large family
(d) Chance of high longevity
Answer:
(d) Chance of high longevity

(II) Fill in the blanks.

Question 1.
An installment of money paid for insurance is called _________
Answer:
premium

Question 2.
General insurance covers all risks except _________
Answer:
life

Question 3.
The value of insured property is called _________
Answer:
property value

Question 4.
The proportion of property value to insured is called _________
Answer:
policy value

Question 5.
The person who receive annuity is called _________
Answer:
Annuitant

Question 6.
The payment of each single annuity is called _________
Answer:
installment

Question 7.
The intervening time between payment of two successive installments is called as _________
Answer:
payment period

Question 8.
An annuity where payments continue forever is called _________
Answer:
perpetuity

Question 9.
If payments of an annuity fall due at the beginning of every period, the series is called _________
Answer:
annuity due

Question 10.
If payments of an annuity fall due at the end of every period, the series is called annuity _________
Answer:
immediate

(III) State whether each of the following is True or False.

Question 1.
General insurance covers life, fire, and theft.
Answer:
False

Question 2.
The amount of claim cannot exceed the amount of loss.
Answer:
True

Question 3.
Accident insurance has a period of five years.
Answer:
False

Question 4.
Premium is the amount paid to the insurance company every month.
Answer:
True

Question 5.
Payment of every annuity is called an installment.
Answer:
False

Question 6.
Annuity certainly begins on a fixed date and ends when an event happens.
Answer:
True

Question 7.
Annuity contingent begins and ends on certain fixed dates.
Answer:
False

Question 8.
The present value of an annuity is the sum of the present value of all installments.
Answer:
True

Question 9.
The future value of an annuity is the accumulated value of all installments.
Answer:
False

Question 10.
The sinking fund is set aside at the beginning of a business.
Answer:
True

(IV) Solve the following problems.

Question 1.
A house valued at ₹ 8,00,000 is insured at 75% of its value. If the rate of premium is 0.80%. Find the premium paid by the owner of the house. If the agent’s commission is 9% of the premium, find the agent’s commission.
Solution:
Property value = ₹ 8,00,000
Policy value = 75% × 8,00,000 = ₹ 6,00,000
∵ Rate of Premium = 0.80%
∴ Amount of Premium = 0.80% × 6,00,000 = ₹ 4,800
∵ Rate of commission = 9%
∴ Agent commission = 9% × 4800 = ₹ 432

Question 2.
A shopkeeper insures his shop and godown are valued at ₹ 5,00,000 and ₹ 10,00,000 respectively for 80% of their values. If the rate of premium is 8%, find the total annual premium.
Solution:
Property value of shop = ₹ 5,00,000
∴ Policy value = 80% × 5,00,000 = ₹ 4,00,000
∵ Rate of Premium = 8%
∴ Amount of premium = 8% × 4,00,000 = ₹ 32,000
∵ Property value of Godown = ₹ 10,00,000
∴ Policy value = 80% × 10,00,000 = ₹ 8,00,000
∵ Rate of Premium = 8%
∴ Amount of Premium = 8% × 8,00,000 = ₹ 64,000
∴ Total annual Premium = 64,000 + 32,000 = ₹ 96,000

Question 3.
A factory building is insured for \(\left(\frac{5}{6}\right)^{\text {th }}\) of its value at a rate of premium of 2.50%. If the agent is paid a commission of ₹ 2,812.50, which is 7.5% of the premium, find the value of the building.
Solution:
Let the Property value be ₹ x
∴ Policy value = ₹ \(\frac{5 x}{6}\)
∵ Rate of premium = 2.50%
∴ Amount of premium = \(\frac{5 x}{6}\) × 2.50% = ₹ \(\frac{x}{48}\)
∵ Rate of Agent commission = 7.5%
∴ Agent commission = 7.5% × \(\frac{x}{48}\)
∴ 2812.50 = \(\frac{x}{640}\)
∴ 2812.50 × 640 = x
∴ x = ₹ 18,00,000
∴ Value of the building is ₹ 18,00,000.

Question 4.
A merchant takes a fire insurance policy to cover 80% of the value of his stock. Stock worth ₹ 80,000 was completely destroyed in a fire. While the rest of the stock was reduced to 20% of its value. If the proportional compensation under the policy was ₹ 67,200, find the value of the stock.
Solution:
Let the Property value be ₹ x
∴ Policy value 80% × x = ₹ \(\frac{4 x}{5}\)
∵ Complete loss = ₹ 80,000
∴ Partial loss = 20% × (x – 8,00,000) = \(\frac{x-80,000}{5}\)
∴ Total loss = 80,000 + \(\frac{x-80,000}{5}\) = \(\frac{x}{5}\) + 64,000
∵ Claim = ₹ 67,200

∴ x = ₹ 1,00,000
∴ The value of the stock is ₹ 1,00,000.

Question 5.
A 35-year old person takes a policy for ₹ 1,00,000 for a period of 20 years. The rate of premium is ₹ 76 and the average rate of bonus is ₹ 7 per thousand p.a. If he dies after paying 10 annual premiums, what amount will his nominee receive?
Solution:
Policy value = ₹ 1,00,000
Period of Policy = 20 years
∵ Rate of premium = ₹ 76 per thousand
∴ Amount of premium = \(\frac{76}{1,000}\) × 1,00,000 = ₹ 7,600
∴ Total Premium = 7,600 × 10 = ₹ 76,000
∴ Rate of Bonus = ₹ 7 per thousand p.a
∴ Total Bonus = \(\frac{7}{1,000}\) × 1,00,000 = ₹ 7,000
∴ Amount received by Nominee = Policy value + Bonus earned
= 1,00,000 + 7,000
= ₹ 1,07,000

Question 6.
15,000 articles costing ₹ 200 per dozen were insured against fire for ₹ 1,00,000. If 20% of the articles were burnt completely and 2,400 other articles were damaged to the extent of 80% of their value, find the amount that can be claimed under the policy.
Solution:
Total Articles = 15,000
∴ Property value = \(\frac{15,000}{12}\) × 200 = 2,50,000
∵ Policy value = ₹ 1,00,000
∴ Complete loss = 20% × 2,50,000 = ₹ 50,000
∴ Partial loss = 80% × \(\frac{2,400}{12}\) × 200 = ₹ 3,20,000
∴ Total loss = 32,000 + 50,000 = ₹ 82,000
∴ Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{1,00,000}{2,50,000}\) × 82,000
= ₹ 32,800

Question 7.
For what amount should a cargo worth ₹ 25,350 be insured so that in the event of a total loss, its value, as well as the cost of insurance, may be recovered when the rate of premium is 2.5%.
Solution:
Let the policy value be ₹ 100 which includes the cost of insurance and premium
∴ Property value = 100 – 2.50 = ₹ 97.50
If the value of the cargo is ₹ 97.50, then the policy value is ₹ 100.
If the value of the cargo is ₹ 25,350, then
Policy value = \(\frac{100 \times 25,350}{97.50}\) = ₹ 26,000

Question 8.
A cargo of grain is insured at \(\left(\frac{3}{4}\right)\)% to cover 70% of its value. ₹1,008 is the amount of premium paid. If the grain is worth ₹ 12 per kg, how many kg of the grain did the cargo contain?
Solution:
Let the Property value be ₹ x
∴ policy value = 70% × x = ₹ \(\frac{7 x}{10}\)
∵ Rate of premium = \(\frac{3}{4}\)%
∴ Amount of premium = Rate × Policy value

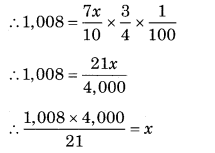
∴ x = ₹ 1,92,000
∵ Rate of Jowar = ₹ 12/kg
∴ Quantity of Jowar = \(\frac{1,92,000}{12}\) = 16,000 kgs

Question 9.
4,000 bedsheets worth ₹ 6,40,000 were insured for \(\left(\frac{3}{7}\right)^{t h}\) of their value. Some of
the bedsheets were damaged in the rainy season and were reduced to 40% of their value. If the amount recovered against damage was ₹ 32,000. Find the number of damaged bedsheets.
Solution:
∵ Property value = ₹ 6,40,000
∴ Policy value = 6,40,000 × \(\frac{3}{7}\) = ₹ \(\frac{19,20,000}{7}\)
∴ Cost of one Bedsheet = \(\frac{6,40,000}{4,000}\) = ₹ 160
Let ‘x’ bedsheets be damaged.
∴ Cost of x bedsheets = ₹ 160x

∴ 875 Bedsheets damaged.

Question 10.
A property valued at ₹ 7,00,000 is insured to the extent of ₹ 5,60,000 at \(\left(\frac{5}{8}\right)\)% less 20%. Calculate the saving made in the premium. Find the amount of loss that the owner must bear, including premium, if the property is damaged to the extent of 40% of its value.
Solution:
∵ Property value = ₹ 7,00,000
∵ Policy value = ₹ 5,60,000
∵ Rate of premium = \(\frac{5}{8}\)%
∴ Amount of premium = \(\frac{5}{8}\)% × 5,60,000 = ₹ 3,500
New rate of premium = \(\frac{5}{8}\)% less 20%
= \(\frac{5}{8}\) – [20% x \(\frac{5}{8}\)]
= \(\frac{5}{8}\) – \(\frac{1}{8}\)
= \(\frac{1}{2}\)%
∴ Amount of premium = \(\frac{1}{2}\)% × 5,60,000 = ₹ 2,800
∴ Saving made in premium = 3,500 – 2,800 = ₹ 700
∴ Loss = 7,00,000 × 40% = 2,80,000
∴ Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{5,60,000}{7,00,000}\) × 2,80,000
= ₹ 2,24,000
∴ Loss bear by owner = loss – claim + premium
= 2,80,000 – 2,24,000 + 2,800
= ₹ 58,800

Question 11.
Stocks in a shop and godown worth ₹ 75,000 and ₹ 1,30,000 respectively were insured through an agent who receive 15% of the premium as commission. If the shop was insured for 80% and godown for 60% of the value, find the amount of agent’s commission when the premium was 0.80% less 20%. If the entire stock in the shop and 20% stock in the godown is destroyed by fire, find the amount that can be claimed under the policy.
Solution:
∵ Rate of premium = 0.80% less 20%
= 0.80 – 20% × 0.80
= 0.80 – 0.16
= 0.64%
For Shop
∵ Property value = ₹ 75,000
∴ Policy value = 80% × 75,000 = ₹ 60,000
∴ Premium = 0.64% × 60,000 = ₹ 384
∵ Loss = ₹ 75,000
∵ Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{60,000}{75,000}\) × 75,000
= ₹ 60,000
For Godown
∵ Property value = ₹ 1,30,000
∴ Policy value = 60% × 1,30,000 = ₹ 78,000
∴ Premium = 0.64% × 78,000 = ₹ 499.2
Loss = 20% × 1,30,000 = ₹ 26,000
∴ Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{78,000}{1,30,000}\) × 26,000
= ₹ 15,600
Total claim = 16,600 + 60,000 = ₹ 75,600
∵ Rate of commission = 15%
∴ Agent commission = 15% × [384 + 499.2]
= 15% × 883.2
= ₹ 132.48

Question 12.
A person holding a life policy of ₹ 1,20,000 for a term of 25 years wants to discontinue after paying a premium for 8 years at the rate of ₹ 58 per thousand p.a. Find the amount of paid-up value he will receive on the policy. Find the amount he will receive if the surrender value granted is 35% of the premium paid, excluding the first year’s premium.
Solution:
Policy value = ₹ 1,20,000
∵ Rate of premium = ₹ 58 per thousand p.a.
∴ Premium for 8 years = \(\frac{8 \times 58}{1000}\) × 1,20,000 = ₹ 55,680
∴ Amount of 1st premium = \(\frac{55,680}{8}\) = ₹ 6,960
∵ Paid-up value of policy = \(\frac{\text { No of Premium paid }}{\text { Terms of policy }}\) × Policy value
= \(\frac{8}{25}\) × 1,20,000
= ₹ 38,400
∵ Surrender value = 35% × [Total premium – 1st year premium]
= 35% × [55,680 – 6,960]
= 35% × 48,720
= ₹ 17,052

Question 13.
A godown valued at ₹ 80,000 contained stock worth ₹ 4,80,000. Both were insured against fire. Godown for ₹ 50,000 and stock for 80% of its value. A part of stock worth ₹ 60,000 was completely destroyed and the rest was reduced to 60% of its value. The amount of damage to the godown is ₹ 40,000. Find the amount that can be claimed under the policy.
Solution:
For Godown
∵ Property value = ₹ 80,000
∵ Policy value = ₹ 50,000
∵ Loss = ₹ 40,000
∵ Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{50,000}{80,000}\) × 40,000
= ₹ 25,000
For stock
∵ Property value = ₹ 4,80,000
∵ Policy value = 80% × 4,80,000 = ₹ 3,84,000
∵ Complete loss = ₹ 60,000
∴ Partial loss = (100 – 60)% × [4,80,000 – 60,000]
= 40% × 4,20,000
= ₹ 1,68,000
∴ Total loss = 1,68,000 + 60000 = ₹ 2,28,000
∴ Claim = \(\frac{\text { Policy value }}{\text { Property value }}\) × Loss
= \(\frac{3,84,000}{4,80,000}\) × 2,28,000
= ₹ 1,82,400
∴ Total claim = 25,000 + 1,82,400 = ₹ 2,07,400

Question 14.
Find the amount of an ordinary annuity if a payment of ₹ 500 is made at the end of every quarter for 5 years at the rate of 12% per annum compounded quarterly. [Given: (1.03) ²⁰ = 1.8061]
Solution:
∵ C = ₹ 500
∵ r = 12% p.a. compounded quarterly,
∴ r = \(\frac{12}{4}\) = 3%
∵ n = 5 years
But, payment is made quarterly
∴ n = 5 × 4 = 20

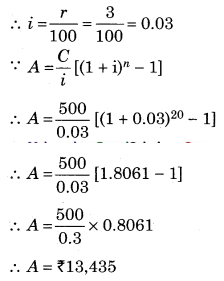
Question 15.
Find the amount a company should set aside at the end of every year if it wants to buy a machine expected to cost ₹ 1,00,000 at the end of 4 years and interest rate is 5% p.a. compounded annually.
Solution:
∵ A = ₹ 1,00,000
∵ r = 5% p.a.
∴ i = \(\frac{r}{100}=\frac{5}{100}\) = 0.05
∵ n = 4 years
∵ A = \(\frac{C}{i}\left[(1+\mathrm{i})^{n}-1\right]\)
∴ 1,00,000 = \(\frac{C}{0.05}\)[(1 + 0.05) ⁴ – 1]
∴ 1,00,000 × 0.05 = C [(1.05) ⁴ – 1]
∴ 5,000 = C(1.2155 – 1)
∴ 5,000 = C × 0.2155
∴ \(\frac{5,000}{0.2155}\) = C
∴ C = ₹ 23,201.86

Question 16.
Find the least number of years for which an annuity of ₹ 3,000 per annum must run in order that its amount exceeds ₹ 60,000 at 10%compounded annually. [Given: (1.1) ¹¹ = 2,8531, (1.1) ¹² = 3.1384]
Solution:
∵ A = ₹ 60,000
∵ C = ₹ 3,000
∵ r = 10% p.a.
∴ i = \(\frac{r}{100}=\frac{10}{100}\) = 0.1
∵ A = \(\frac{C}{i}\left[(1+i)^{n}-1\right]\)
∴ 60,000 = \(\frac{3,000}{0.1}\left[(1+0.1)^{n}-1\right]\)
∴ 60,000 = 30,000[(1.1) ⁿ – 1]
∴ \(\frac{60,000}{30,000}\) + 1 = (1.1) ⁿ
∴ 2 + 1 = (1.1) ⁿ
∴ 3 = (1.1) ⁿ
Taking log
∴ log 3 = log (1.1) ⁿ
∴ log 3 = n log(1.1)
∴ \(\frac{\log 3}{\log 1.1}\) = n
∴ n = \(\frac{0.4771}{0.0414}\) = 11.52 ~ 12 years

Question 17.
Find the rate of interest compounded annually if an ordinary annuity of ₹ 20,000 per year amounts to ₹ 41,000 in 2 years.
Solution:
∵ C = ₹ 20,000
∵ A = ₹ 41,000
∵ n = 2 years

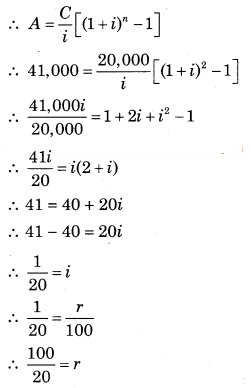
∴ r = 5% p.a.

Question 18.
A person purchases a television by paying ₹ 20,000 in cash and promising to pay ₹ 1,000 at the end of every month for the next 2 years. If money is worth 12% p.a., converted monthly. Find the cash price of the television. [Given: (1.01) ^-24 = 0.7880]
Solution:
Down payment = ₹ 20,000
∵ n = 2 years
But, EMI Payable monthly
∴ n = 2 × 12 = 24
∵ r = 12% p.a. compounded monthly

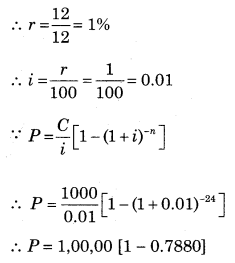
∴ P = 1,00,00 × 0.2120
∴ P = ₹ 21,200
Cash price = Present value + Down payment
= 21,200 + 20,000
= ₹ 41,200

Question 19.
Find the present value of an annuity immediate of ₹ 20,000 per annum for 3 years at 10% p.a. compounded annually. [Given: (1.1) ^-3 = 0.7513]
Solution:
∵ C = ₹ 20,000
∵ n = 3 years
∵ r = 10% p.a.

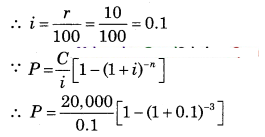
∴ P = 2,00,000 [1 – 0.7513]
∴ P = 2,00,000 [0.2487]
∴ P = ₹ 49,740

Question 20.
A man borrowed some money and paid it back in 3 equal installments of ₹ 2,160 each. What amount did he borrow if the rate of interest was 20% per annum compounded annually? Also, find the total interest charged. [Given: (1.2) ^-3 = 0.5788]
Solution:
∵ C = ₹ 2,160
∵ n = 3
∵ r = 20% p.a.

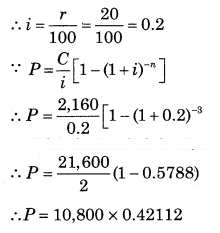
∴ P = ₹ 6,251.04
∴ Total amount paid = 2,160 × 3 = ₹ 6,480
∴ Interest = 6,480 – 6,251.04 = ₹ 228.96

Question 21.
A company decides to set aside a certain amount at the end of every year to create a sinking fund that should amount to ₹ 9,28,200 in 4 years at 10% p.a. Find the amount to be set aside every year. [Given: (1.1) ⁴ = 1.4641]
Solution:
∵ A = ₹ 9,28,200
∵ n = 4 years
∵ r = 10% p.a.

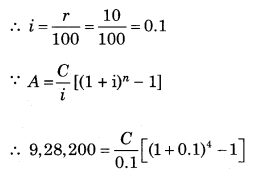
∴ 9,28,200 × 0.1 = C[1.4641 – 1]
∴ 92,820 = C × 0.4641
∴ \(\frac{92,820}{0.4641}\) = C
∴ C = ₹ 2,00,000

Question 22.
Find the future value after 2 years if an amount of ₹ 12,000 is invested at the end of every half-year at 12% p.a. compounded half-yearly. [Given: (1.06) ⁴ = 1.2625]
Solution:
∵ n = 2 years
Payable half yearly, n = 2 × 2 = 4
∵ C = ₹ 12,000
∵ r = 12% p.a. Compounded half yearly


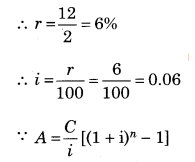
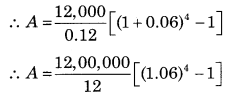
∴ A = 1,00,000 [1.2625 – 1]
∴ A = 1,00,000 × 0.2625
∴ A = ₹ 26,250

Question 23.
After how many years would an annuity due of ₹ 3,000 p.a. accumulated ₹ 19,324.80 at 20% p.a. compounded annually? [Given: (1.2) ⁴ = 2.0736]
Solution:
∵ C = ₹ 3,000
∵ A = ₹ 9,324.80
∵ r = 20% p.a.

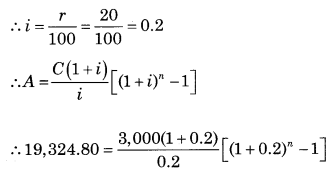
∴ 19,324.80 = 15,000 × 1.2[(1.2) ⁿ – 1]
∴ 19,324.80 = 18,000[(1.2) ⁿ – 1]
∴ \(\frac{19,324.80}{18,000}\) + 1 = (1.2) ⁿ
∴ 1.0736 + 1 = (1.2) ⁿ
∴ 2.0736 = (1.2) ⁿ
∴ (1.2) ⁴ = (1.2) ⁿ
∴ n = 4 years

Question 24.
Some machinery is expected to cost 25% more over its present cost of ₹ 6,96,000 after 20 yeas. The scrap value of the machinery will realize ₹ 1,50,000. What amount should be set aside at the end of every year at 5% p.a. compound interest for 20 years to replace the machinery? [Given: (1.05) ²⁰ = 2655]
Solution:
Present cost = ₹ 6,96,000
Expected cost = 25% × 6,96,000 + 6,96,000
= 1,74,000 + 6,96,000
= ₹ 8,70,000
∴ Scrap value = ₹ 1,50,000
∴ Sinking fund = 8,70,000 – 1,50,000 = ₹ 7,20,000
∴ A = ₹ 7,20,000, n = 20 years, r = 5% p.a.

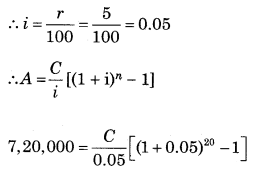
∴ 7,20,000 × 0.05 = C[(1.05) ²⁰ – 1]
∴ 36,000 = C[2.655 – 1]
∴ 36,000 = C × 1.655
∴ \(\frac{36,000}{1.655}\) = C
∴ C = ₹ 21,752.27